В статье рассматривается теорема Пикара и доказывается единственность решения задачи Коши.
Ключевые слова: теорема Пикара, единственность решения задачи Коши, условие Липшица.
Постановка задачи Коши
Рассмотрим задачу Коши
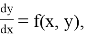
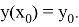
Функция
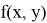
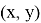
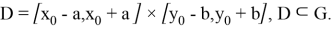
1)
Пусть

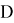
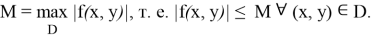
2)
Пусть
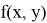
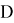
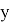
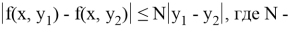
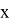
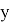
Замечание. Условие Липшица будет выполнено, в частности, если
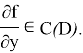
Очевидно, что если интегральная кривая, проходящая через точку

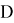
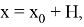
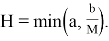
Действительно, уравнения «крайних» интегральных кривых, удовлетворяющих задаче Коши
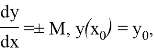
имеют вид
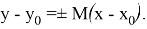
Подставив уравнения горизонтальных границ области
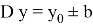
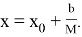
Теорема (существования и единственности решения задачи Коши).
Пусть выполнены условия 1) и 2). Тогда на отрезке
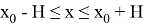
существует единственное решение задачи (1).
Следующее утверждение существенно используется при доказательстве сформулированной теоремы.
Лемма 1.
Пусть
функция
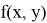
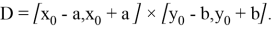
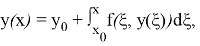
которое рассматривается в классе непрерывных функций.
Доказательство единственности решения задачи Коши.
Для доказательства единственности будет использовано следующее утверждение.
Лемма
(Гронуолла)
.
Пусть
существует постоянная
L
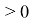
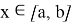
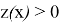
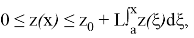
Тогда при
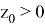
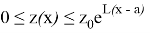
В случае
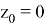

Доказательство:
1) Пусть
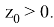
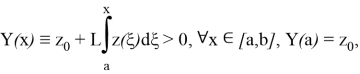
тогда в силу (3) имеем

Так как

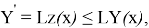

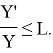
Далее интегрируя, имеем
ln
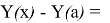
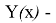
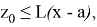
откуда после потенцирования получаем
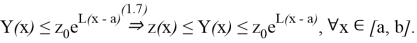
2) Пусть
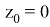
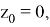
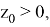
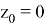
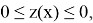
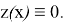
Лемма 2.
Интегральное уравнение (2) имеет единственное решение
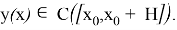
Доказательство:
Предположим, что имеется два различных решения уравнения (2)
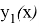

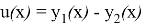
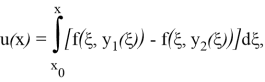
откуда
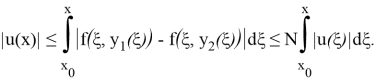
Полагая
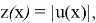
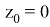
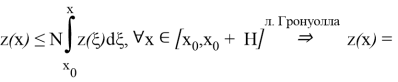
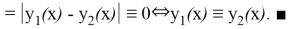
Замечание.
Условие Липшица может быть заменено более удобным требованием наличия непрерывной в
D
(и потому ограниченной) производной
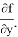
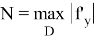
такая, что
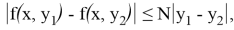
Литература:
- Н. М. Матвеев. Методы интегрирования обыкновенных дифференциальных уравнений. Москва, 2015 г.
- Танкиев И. А. Исследование некоторых краевых задач для счетных систем ОДУ. Диссертация. Баку, 1976 г.







