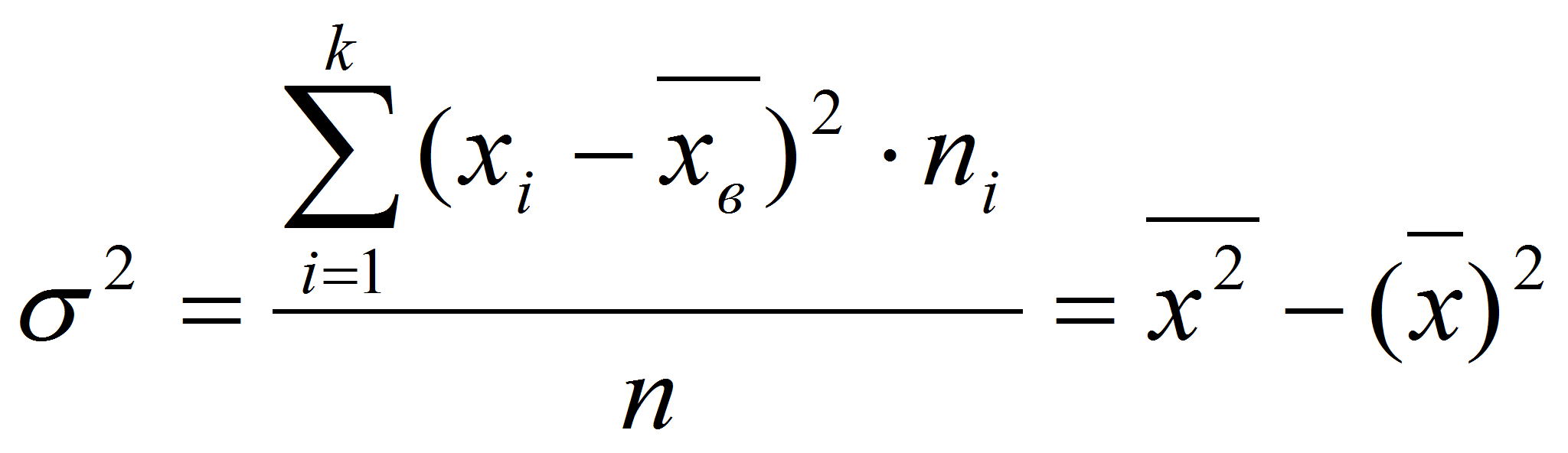Использование статистических методов обработки данных стали привычным и широко распространенным аппаратом для инженеров металлургического производства при оценке результатов механических испытаний, химического состава стали, температурно-деформационных параметров и др. Работа инженера связана с исследованиями производственных процессов и технологий, а поэтому очень важно, чтобы студенты технических специальностей умели решать исследовательские задачи. Исследовательская деятельность инженера заключается в самостоятельном видении технических проблем; выявлении их причин; формулировке гипотез, их проверке с помощью инженерного эксперимента, наблюдения или на основе анализа технических данных и фактов; в выборе из ряда гипотез наиболее рациональной, отвечающей нуждам производства и последующего внедрения их в производственный процесс [4, с.4]. Однако, вследствие формальности изложения дисциплины, студенты, имея даже хороший запас знаний, не всегда могут его использовать в профессиональной деятельности. Мотивация изучения студентами раздела математической статистики может быть обеспечена осознанием ими его значимости для будущей профессии. С этой целью содержание дисциплины целесообразно наполнять учебно-профессиональными исследовательскими задачами - ситуациями, требующими от студентов мыслительных и практических действий, направленных не только на усвоение ими профессиональных знаний и умений, но и на овладение исследовательскими умениями, на приобретение опыта исследовательской деятельности.
Ориентация на практическое использование знаний предполагает постановку задач с учетом будущей профессиональной деятельности студента, подбор конкретного материала и выбор формы организации работы [2, с. 121]. Новотроицкий филиал «МИСиС» готовит специалистов по заказу металлургического комбината ОАО «Урал Сталь», это позволяет тесно взаимодействовать преподавателям и студентам с предприятием. Преподавателями кафедры математики и естествознания Новотроицкого филиала НИТУ «МИСиС» была организована работа с центральной лабораторией комбината, что позволило выявить аппарат математической статистики, используемый в исследованиях металлургического производства. Рассмотрим некоторые его ключевые понятия и средства.
Одним из основных понятий является выборочная совокупность – понятие, лежащее в основе всех статистических методов, и представляющее собой часть объектов из генеральной совокупности, отобранных для изучения. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна быть представительной. Значительные объемы производства металлопроката, стабилизация технологического процесса производства позволили сформировать представительную выборочную совокупность и разработать математические модели для расчета уровня механических свойств в зависимости от углеродного эквивалента, химического состава стали и технологических параметров прокатки. Чтобы обеспечить однородность выборочной совокупности необходимо учитывать следующие факторы:
- нормативную документацию;
- марку стали;
- период времени;
- агрегат выплавки;
- состояние поставки.
В качестве одного из важнейших параметров статистики является средняя
величина (арифметическая, геометрическая, гармоническая,
квадратичная, кубическая). Чаще используют арифметическую среднюю,
вычисляемую по формуле:
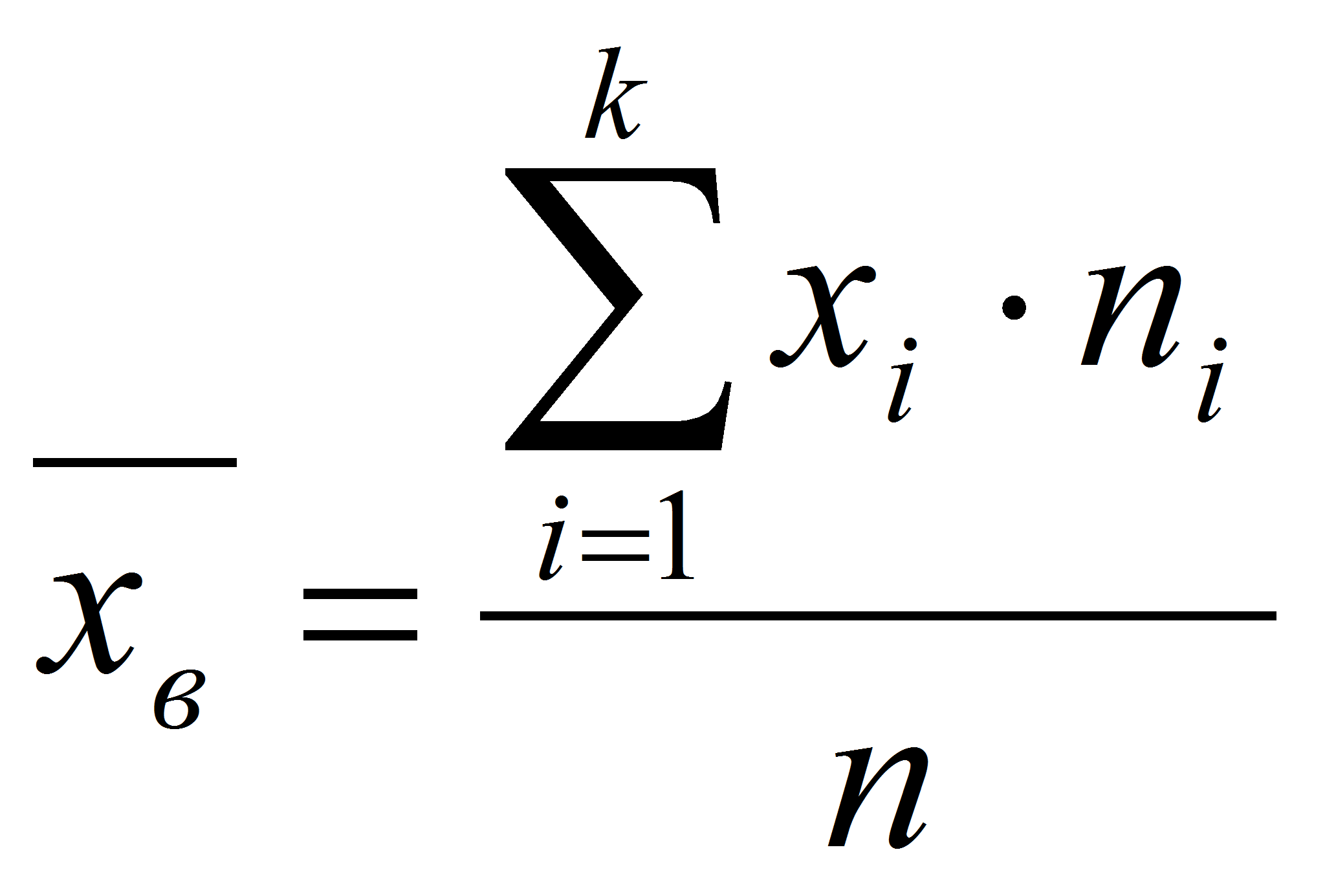
Средние величины, характеризуя частотный ряд одним числом, не учитывают разброса признака. Для измерения колебания признака используют вариационный размах, дисперсию и среднее квадратическое отклонение. Вариационный размах R есть разность между экстремальными значениями частотного ряда: R=xmax -xmin. Вариационный размах – величина неустойчивая, зависящая от случайных обстоятельств. Дисперсия – средняя арифметическая из квадратов отклонений вариантов от их средней арифметической:
По сравнению со значениями случайной величины, дисперсия измеряется в
квадратных единицах. Для того чтобы иметь меру рассеяния,
сопоставимую со значениями средней величины, используют среднее
квадратическое отклонение случайной величины:
![]() .
.
Характеристикой колеблемости признака служат
относительные показатели, например, коэффициент вариации:
![]() .
Коэффициент вариации представляет собой относительную меру
рассеивания, выраженную в процентах.
.
Коэффициент вариации представляет собой относительную меру
рассеивания, выраженную в процентах.
Наблюдая многочисленные ряды распределения, исследователи стремятся
построить теоретическое распределение, исходя из данных эмпирического
распределения. Теоретическим законом многих рядов, встречаемых на
практике, является нормальное распределение, которое зависит
от средней арифметической и квадратического отклонения. Это
объясняется теоремой А.М. Ляпунова: если случайная величина
представляет собой сумму большого числа взаимно независимых случайных
величин, влияние каждой из которых на всю сумму ничтожно, то величина
имеет распределение, близкое к нормальному [1, с.135]. Умение выявить
нормальное распределение в некотором эмпирическом ряде является
важным условием для практических расчетов. Зная, что фактическое
распределение является нормальным, можно определить оптимальные
размеры резервов, оптимальное содержание элементов химического
состава в металле. Для того чтобы определить, является ли данное
распределение нормальным, используют специально подобранные случайные
величины, называемые критериями согласия. В технических исследованиях
наиболее часто употребляемыми являются критерии Пирсона, Стьюдента,
Романовского, Колмогорова и др. Для оценки близости эмпирического
распределения к теоретическому, используется критерий Пирсона
проверки гипотезы о нормальном распределении генеральной
совокупности. С этой целью сравнивают эмпирические (наблюдаемые) и
теоретические (вычисленные в предположении нормального распределения)
частоты. Случайная величина имеет вид:
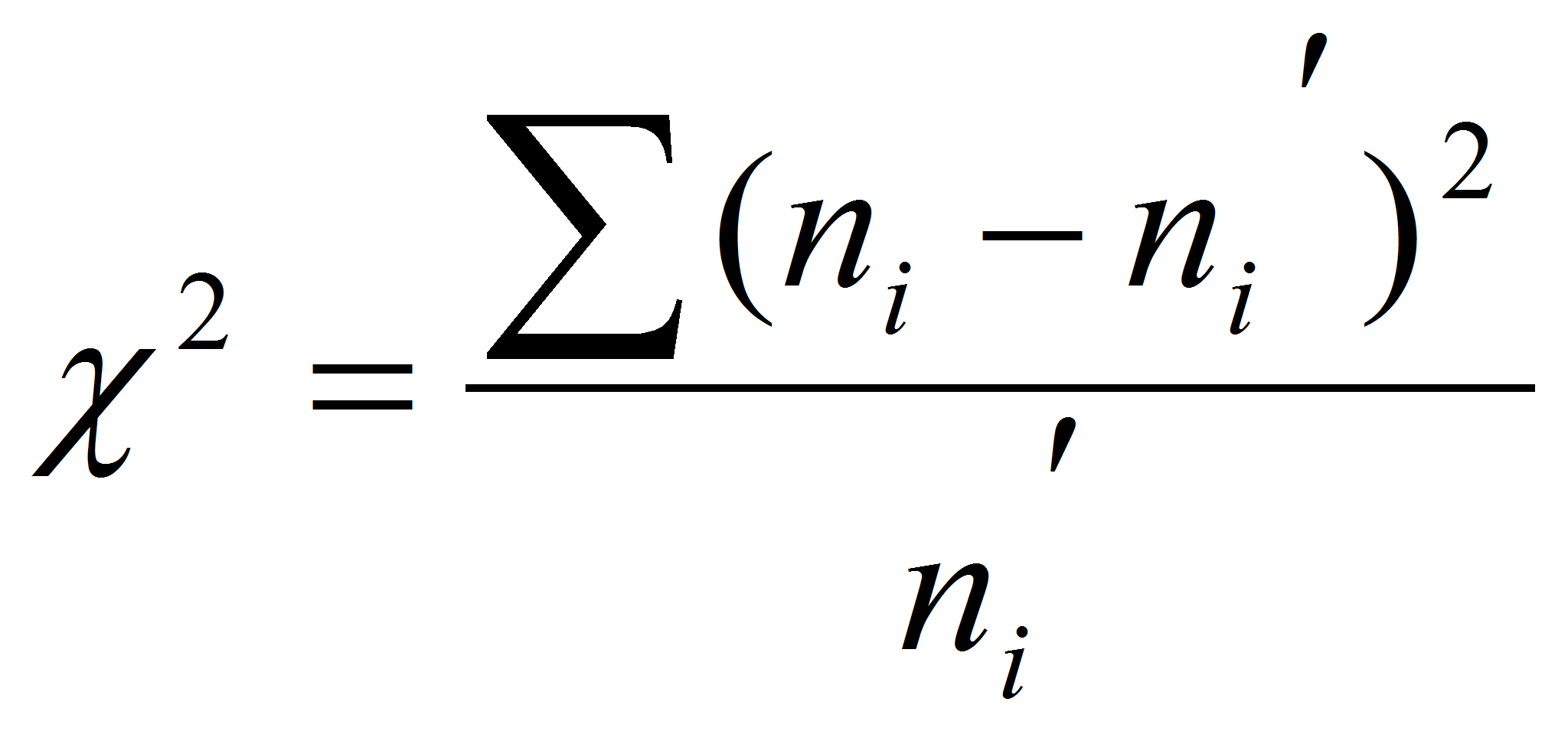 .
.
Чем меньше различаются эмпирические и теоретические частоты, тем меньше значение критерия, что свидетельствует о близости эмпирического и теоретического распределений.
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. Оценку
можно произвести с помощью характеристик: асимметрии (As
– свидетельствует о симметрии кривой распределения) и эксцесса
(Ek
– оценка «крутости» кривой, то есть большего
лил меньшего подъема кривой распределения относительно нормальной
кривой) [3, с. 158]:
![]() ,
где
,
где
![]() ;
;
![]() .
.
Для нормального распределения эти величины нулевые. Если асимметрия и эксцесс – небольшие величины, это свидетельствует о близости распределения к нормальному.
С помощью рассмотренного аппарата математической статистики возможно оценить статистические параметры и построить частотные распределения массовой доли химических элементов в различных видах стали и механических свойств (характеристик растяжения: предела текучести, временного сопротивления, относительного удлинения; вязких свойств – ударной силы). Статистические данные по механическим свойствам предназначены:
- для анализа показателей качества выпускаемой продукции;
- дальнейшего совершенствования технологии производства;
- улучшения качественных показателей металлопродукции;
- для подбора оптимальной марки-аналога на основе идентично производимой и сопоставимой продукции по механическим свойствам.
Чтобы выявить взаимосвязь явлений, пользуются результатами корреляционного анализа. Между случайными величинами может существовать как функциональная, так и статистическая связь, при которой с изменением одной величины меняется распределение другой. Выявление статистической связи и оценка её силы представляет важную и трудную задачу математической статистики. Одним из важнейших показателей, оценивающих силу статистической связи, является коэффициент корреляции. В качестве примера статистической связи можно рассмотреть зависимость предела прочности стали (определенной марки) от коэффициента совокупного влияния химического состава.
Наблюдая статистическую связь, исследователи стремятся придать этой связи форму функциональной, то есть определить для связи математическую функцию (например, с использованием метода наименьших квадратов).
Рассмотренные статистические параметры и методы позволяют преподавателю организовать учебно-профессиональную деятельность студентов на основе интеграции методологии профессионального обучения и методологии научного исследования.
Рассмотрим структуру процесса решения учебно-профессиональной исследовательской задачи на примере рассмотрения влияния химического состава (например, содержания углерода) определенной марки стали на предел прочности (таблица).
Таблица
Структура процесса решения учебно-профессиональной исследовательской задачи
|
Этапы решения задачи |
Действия и операции |
|
I. Определение целей и задач исследования на основе анализа условия задачи |
1. Анализ условия задачи: - выделение технических объектов, процессов и явлений, рассматриваемых в задаче; - определение исследуемых признаков; 2. Выделение имеющихся технических противоречий и разбиение задачи на подзадачи: - противоречие между необходимостью определения связи между содержанием углерода и показателей предела прочности стали и отсутствием для этого прямых данных 3. Сбор статистических данных: - массовая доля углерода в рассматриваемой марке стали; - результаты испытаний по механическим свойствам (предел прочности) |
|
II. Выявление взаимосвязей между явлениями и процессами, описанными в задаче, поиск закономерностей, характерных для исследуемых процессов |
- рассмотрение механических свойств стали (характеристик растяжения: предела текучести, временного сопротивления, относительного удлинения; вязких свойств – ударной силы); - определение химических свойств углерода 2. Определение причинно-следственных связей между данными задачи |
|
III. Формулирование гипотезы (либо ряда предположений) согласно целям исследования |
|
|
IV. Проверка гипотезы (с помощью выбранной математической модели) |
Реализация методики исследования: - построение корреляционного поля точек (функция- предел прочности, аргумент – содержание углерода в металле); - расчет выборочных средних; - расчет средних квадратических отклонений; - расчет коэффициента корреляции; - расчет коэффициента регрессии; - расчет свободного члена уравнения. |
|
V. Анализ и оценка полученных результатов |
1. Проверка правильности расчетов, выбранной формы связи: - построение эмпирической и теоретической линий регрессий (в каждом интервале значений аргумента рассчитывается среднее значение функции, и, соединяя точки средних, получаем эмпирическую линию регрессии; по полученному уравнению строим теоретическую линию регрессии; если теоретическая линия регрессии хорошо вписывается в эмпирическую, то полученное уравнение правильно описывает данную зависимость) 2. Рассмотрение результата для частных случаев и предельных значений. 3. Осмысление процесса получения данного решения. 4. Указание области практического применения выделенных технических объектов и оценка их эффективности |
Тесное сотрудничество с предприятием, для которого готовятся специалисты, использование учебно-профессиональных исследовательских задач, организация исследовательской деятельности студентов формирует исследовательские навыки, что позволит будущим инженерам успешно проводить инженерный эксперимент, модернизировать производственные технологии и повышать технико-экономические показатели.
Литература:
Гмурман, В.Е. Теория вероятностей и математическая статистика. Учеб. Пособие для вузов. – изд. 7-е, стер. – М.: Высш. шк., 2001. – 479 с.
Земцова, В.И. Управление учебно-профессиональной деятельностью студентов на основе функционально-деятельностного подхода: Монография. – М.: Компания Спутник+, 2008. – 208 с.
Калинина, В.Н., Панкин, В.Ф. Математическая статистика: Учеб. Для сту. Сред. Спец. Учеб. Заведений. – 3-е изд., испр. – М.: Высш. шк., 2001. – 336 с.
Методика решения учебно-профессиональных исследовательских задач при изучении естественнонаучных дисциплин (на примере курса общей физики): методические рекомендации для студентов технических специальностей / сост. И. А. Ткачева. – Орск : Издательство ОГТИ, 2009. – 63 с.