Оценивание параметров генеральных совокупностей методом малых выборок по критерию Стьюдента с помощью шаблонов Excel



Рассмотрено применение метода малых выборок для оценивания генеральных совокупностей по распространенному критерию Стьюдента. Указываются отличия при статистическом оценивании выборок малого объема методами нормального распределения и t-распределения.

Рассмотрены конкретные примеры применения шаблонов Excel при анализе реальных результатов измерений резисторов по номинальному значению сопротивления и их преимущества перед ручным счетом при принятии решений о годности контролируемых объектов.

Ключевые слова: генеральная совокупность, малая выборка, критерий Стьюдента, нормальное распределение, шаблоны Excel.

В результате различных экспериментов исследователи получают данные, которые группируют в статистические ряды. Первым этапом исследования статистических рядов является ответ на вопрос, к какому виду распределения относятся полученные результаты. В зависимости от предполагаемого вида распределения производится вычисление основных статистических характеристик: средней арифметической величины (математического ожидания), дисперсии, среднего квадратического отклонения. Идеальным экспериментом является изучение совокупности всех объектов для решения поставленной задачи, то есть генеральной совокупности. В действительности число членов такой совокупности может быть бесконечно большим, поэтому на практике изучают выборочные совокупности, а затем на этой основе делают выводы об изучаемой генеральной совокупности.

В этом случае необходимо ответить на вопрос, насколько параметры данной выборки соответствуют параметрам генеральной совокупности, то есть, вычисляя параметры конкретной выборки, дать оценку соответствующих параметров генеральной совокупности. При определении доверительного интервала для генеральной средней в этом случае нужно пользоваться статистическими таблицами для нормального интеграла вероятностей. Если число членов в выборке мало (меньше 30), то возникает сомнение в возможности оценки по таким выборкам параметров генеральной совокупности. При формировании объема выборки можно придерживаться общего подхода, полагая, что она должна составлять 5–10 % (реже 15–25 %) от объема генеральной совокупности.

Принято считать, что начало статистике малых выборок или, как ее часто называют, статистике «малых n », было положено в 1908 г. публикацией работы сотрудника английской пивоваренной компании Уильяма Госсета, в которой он поместил t -распределение, постулированное получившим чуть позже мировую известность «студентом». Госсет опубликовал результаты своего эксперимента по сравнению выборочного контроля качества пива для проведения химического анализа с использованием t -распределения для малых выборок и традиционного z -распределения (нормального распределения) анонимно, под псевдонимом «Стьюдент» (Student). Рональд Фишер в дальнейшем использовал распределение в своих работах и дал ему название t -распределение Стьюдента, которое связывает между собой три основных характеристики выборочной совокупности: ширину доверительного интервала, соответствующую ему доверительную вероятность и объем выборки. В частности, на основе распределения Стьюдента можно получить надежную оценку доверительного интервала для аттестованного значения образца для контроля.

Теория t -распределения, подобно теории z -распределения, используется для проверки нулевой гипотезы о том, что две выборки представляют собой просто случайные выборки из одной генеральной совокупности и, следовательно, вычисленные статистики (например, среднее и стандартное отклонение) являются несмещенными оценками параметров генеральной совокупности. Однако, в отличие от теории нормального распределения, теория t -распределения для малых выборок не требует априорного знания или точных оценок математического ожидания и дисперсии генеральной совокупности. Более того, хотя проверка различия между средними двух больших выборок на статистическую значимость требует принципиального допущения о нормальном распределении характеристик генеральной совокупности, теория t -распределения не требует допущений относительно параметров.

Если случайная величина Х распределена по закону , то она называется стандартизованной нормальной величиной. Общеизвестно, функция распределения стандартизованной гауссовской величины описывается одной единственной кривой — кривой Гаусса, которая удовлетворяет следующему уравнению и называется функцией Лапласа:

(1)

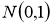
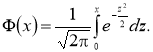
Распределение случайной величины называется распределением Стьюдента с k степенями свободы. Распределение Стьюдента с k степенями свободы имеет плотность , которая выражается следующей формулой [1, с. 238]:

(2)

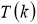
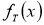
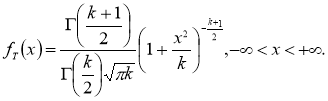
где — гамма-функция. Вот почему уравнение для t включает гамма-функцию, которая в математике означает, что при изменении n данному уравнению будет удовлетворять другая кривая.

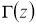
Распределение Стьюдента имеет среднее и дисперсию [1, с. 238].

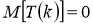
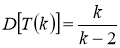
Измерительная задача. Пусть количественный признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.

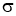
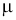
Из литературы [2, с. 190] известно, что по данным выборки можно построить случайную величину (её возможные значения принято обозначать через t):

(3)

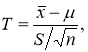
которая имеет распределение Стьюдента с степенями свободы; здесь — выборочная средняя, — «исправленное» среднее квадратическое отклонение, — объем выборки.

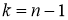
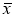
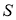
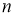
Мы видим из уравнений (2) и (3), что распределение Стьюдента определяется параметром – объемом выборки (или, что то же, числом степеней свободы ) и не зависит от неизвестных параметров и ; эта особенность является его большим достоинством. Поскольку четная функция от t, то вероятность осуществления неравенства

(4)

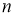
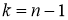
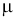
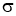
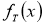
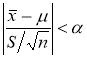
определяется так [3, с. 217]

(5)

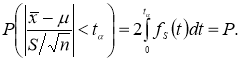
Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим [3, с.217, 4, с. 13]

(6)

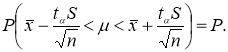
Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал

(7)

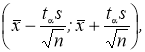
покрывающий неизвестный параметр с надежностью (доверительной вероятностью) P .

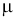
Здесь случайные величины и заменены неслучайными величинами

и , найденными по выборке. По имеющимся в различных источниках [2, с. 234, 3, с. 466] таблицам по заданным объему выборки и доверительной вероятности можно найти и далее найти доверительные границы для неизвестного параметра (по классической схеме при ручном счете).

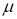
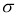
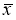
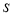
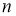
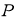
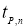
Из литературы [5, с. 191] общеизвестно, что при неограниченном возрастании объема выборки распределение Стьюдента стремится к нормальному. Поэтому практически при можно вместо распределения Стьюдента пользоваться нормальным распределением.

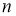
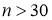
Однако важно подчеркнуть, что для малых выборок ( ), в особенности для малых значений , замена распределения нормальным приводит к грубым ошибкам, а именно, к неоправданному сужению доверительного интервала, т. е., к повышению точности оценки. Например, если

и то пользуясь распределением Стьюдента, найдем а используя функцию Лапласа, найдем т. е., доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

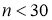
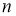
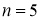
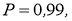
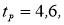
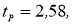
То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

Степени свободы. Число называют числом степеней свободы. Смысл этого параметра в данном случае можно объяснить следующим образом: если имеется вариационный ряд, состоящий из n членов, и была определена средняя арифметическая величина ( ), то каждое отдельное значение можно найти, зная и остальные вариант. То есть имеется степени свободы. При числе опытов n больше либо равном 30 разница между n и

не велика и не отражается на величине дисперсии.

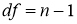
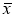
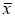
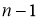
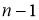
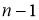
В качестве примера использования распределения Стьюдента при выполнении лабораторных работ, связанных с измерением номинальных значений сопротивлений резисторов, представленных для контроля, рассмотрим обработку данных при помощи разработанного шаблона программного пакета Excel.

Реализация измерительной задачи. В работе производится оценка значений активного сопротивления в генеральной совокупности партий резисторов условным объемом N = 10000 шт. различных номинальных значений по результатам контроля малых выборок объемами n = 5, n = 10, n = 15, n = 25.

Исследованиям подвергались резисторы, приобретенные у ЗАО «ЧИП и ДИП», с номинальными значениями сопротивлений: R _н = 3,9 кОм ± 10 %; R _н = 27,0 кОм ± 5 %; R _н = 220,0 кОм ± 5 %; R _н = 330,0 кОм ± 10 %; R _н = 150,0 кОм ± 5 %; R _н = 51,0 кОм ± 5 %; R _н = 750,0 кОм ± 5 %; R _н = 2,0 МОм ± 5 %.

Учащиеся производили измерения и затем данные результатов измерений заносились в разработанный шаблон Excel с расчетными формулами для определения доверительных интервалов по критерию Стьюдента при доверительных вероятностях Р = 0,95 и 0,99. Шаблон позволяет произвести расчеты в автоматическом режиме, при этом исключаются ошибки счета, что нередко бывает при ручном методе расчета.

Измерения сопротивления резисторов производились цифровыми мультиметрами марки М-832 (рис. 1).

Рис. 1. Общий вид мультиметра М-832

При осуществлении расчетов использовались таблицы вида (см. рис. 2–8). Далее рассмотрен пример обработки данных при R _н = 150,0 кОм ± 5 %.

На скриншотах показана последовательность действий в среде Excel на примере выборки n = 25.

Все действия с другими объемами выборок аналогичны рассмотренному объему n = 25 на рис. 2–8.

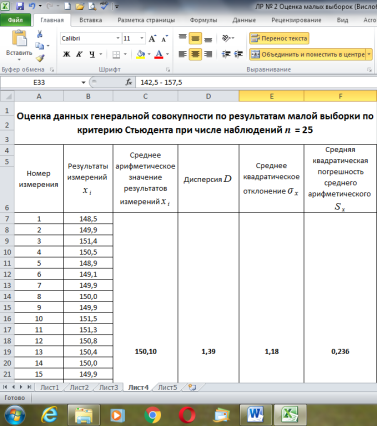
Рис. 2. Фрагмент диалогового окна с результатами измерений

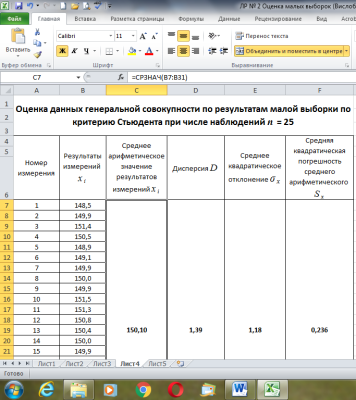
Рис. 3. Определение среднего арифметического значения

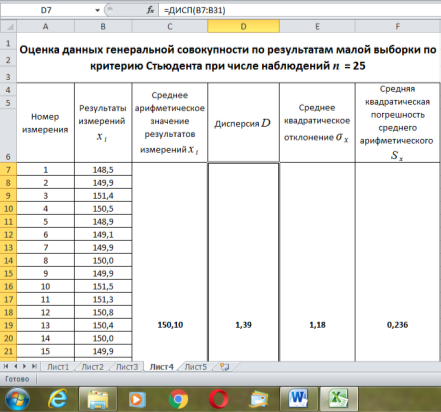
Рис. 4. Определение дисперсии

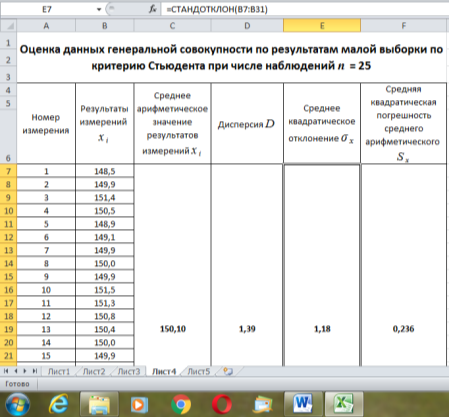
Рис. 5. Определение среднего квадратического отклонения

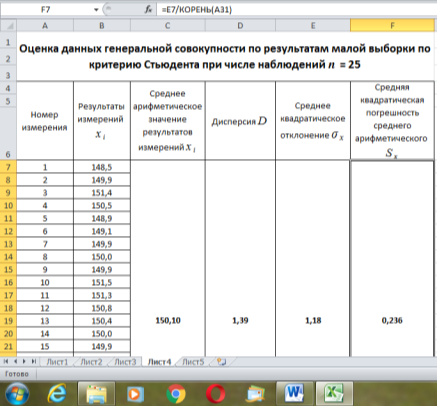
Рис. 6. Определение средней квадратической погрешности среднего арифметического

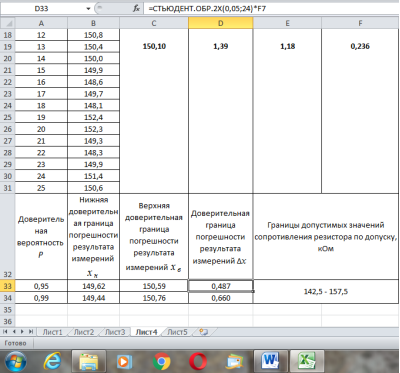
Рис. 7. Определение доверительных границ погрешности результата измерений при доверительной вероятности Р = 0,95

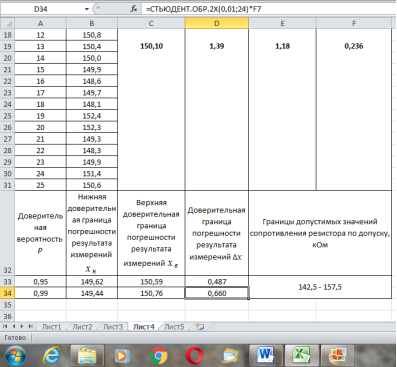
Рис. 8. Определение доверительных границ погрешности результата измерений при доверительной вероятности Р = 0,99

Анализ приведенных на рис. 2–8 данных показал, что во всех случаях значение доверительных границ оказалось в пределах заданных в технических условиях допустимых значений и для других данных номиналов резисторов при доверительных вероятностях Р = 0,95 и Р = 0,99.

Одновременно оказалось, что распределение значений t отличается от нормального, тем сильнее, чем меньше n .

Поэтому и вероятность нахождения выборочных средних в пределах определенных значений значительно снижается по сравнению с нормальным распределением. Так, для доверительной вероятности Р = 0,95 значение t по таблицам для нормального закона распределения равно 1,96 и, следовательно, доверительный интервал:

( ) (8)

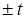
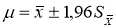
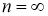
Для числа опытов n = 5 по таблицам Стьюдента t = 2,78. Доверительный интервал:

( ) (9)

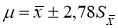
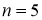
По мере увеличения n, t — распределение Стьюдента приближается к нормальному. При разница между ними практически исчезает. Таблицы t –критерия Стьюдента построены для заданных уровней доверительных вероятностей (уровней значимости) и числа степеней свободы: В программном пакете Excel для вызова нужного значения t -критерия служит функция СТЬЮДЕНТ.ОБР.2Х (критерий значимости; число степеней свободы).

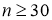
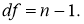
Теперь нужно еще установить, что понимать под малой вероятностью. Ее выбор весьма произволен, но на основе опытов установили определенные границы, которые называются уровнями значимости. Вместо уровня значимости α используют иногда доверительную вероятность:

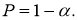
Чаще всего используются следующие уровни значимости: α = 5 % (Р = 95 %), α = 1 % (Р = 99 %) и α = 0,1 % ( Р = 99,9 %).

Отметим, что если расчетное значение статистики Стьюдента меньше или равно табличному значению критерия Стьюдента: t _i ≤ t _{p , f} , то результат считаем удовлетворительным. Если расчетное значение статистики Стьюдента больше табличного значения критерия Стьюдента: t _i > t _{p , f} , то результат считаем неудовлетворительным.

Право выбора величины доверительной вероятности в каждом отдельном случае остается за экспериментатором. На практике не бывает так, чтобы производственный вопрос решался только на основе результата статистического анализа. На первом месте должны всегда стоять практические соображения.

Применение t -критерия только тогда строго обосновано, когда выборка производится из нормально распределенной генеральной совокупности.

Если же распределение генеральной совокупности отличается от нормального, то распределение средних значений, вычисленных по выборкам небольшого объема, приближается к нормальному. Поэтому практически t -критерий применяется также в случае отличия распределения генеральной совокупности от нормального.

При достаточно большом объеме выборки доверительный интервал для математического ожидания равен

. [5, с. 165].

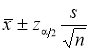
Если объем выборки небольшой, то в приведенной формуле доверительного интервала вместо z подставляют t , большее по величине, которое зависит не только от доверительной вероятности, но и от объема выборки n.

Объем выборки n можно вычислить исходя из определенной доверительной вероятности и точности доверительного интервала [6, с. 83].

(нормальное распределение) или (распределение Стьюдента).

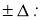
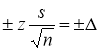
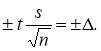
Как видно из рассмотренных примеров и теоретических рассуждений, нахождение доверительных интервалов искомого параметра выходит за чисто статистические рамки и непосредственно переходит в область практической применимости статистических методов управления качеством конкретной продукции [6, с. 77–80]. Заметим, что ошибочное использование t ‐критерия Стьюдента увеличивает вероятность выявить несуществующие различия, т. е. подтвердить недостоверную гипотезу.

Выводы

1. Рассмотрев применение метода малых выборок для оценивания генеральных совокупностей по распространенному критерию Стьюдента, авторы показали его действенность на практике. Это один важнейших статистических методов исследования, позволяющий сделать объективный вывод о сходстве или различии объектов анализа.
2. Применение критериев Стьюдента при оценке генеральных совокупностей больших объемов методами малых выборок позволяет при обработке эмпирических данных принимать конкретные управленческие решения о качестве продукции, поступающей на входной контроль или находящейся на различных стадиях производства в технологическом процессе.
3. Использование таких программных средств, как Excel, при обработке данных и получении конкретных результатов, исключает неизбежные ошибки ручного счета, повышает доверие пользователей к получаемым результатам, у обучающихся — повышает интерес к проводимым исследованиям, а также способствует повышению уровня их подготовки в области статистической обработки результатов измерений.

Литература:

1. Сборник задач по математике для втузов. Специальные курсы. /Коллектив авторов: Э. А. Вуколов, А. В. Ефимов, В. Н. Земсков и др. / Под ред. А. В. Ефимова. — М.: Наука, 1984. — 608 с.
2. Михок Г., Урсяну В. Выборочный метод и статистическое оценивание / Под ред. В. Ф. Матвеева. — М.: Финансы и статистика, 1982. — 245 с.
3. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В. Е. Гмурман. — 9-е изд. стер. М.: Высш. школа, 2003. — 479 с.
4. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
5. Сулицкий В. Н. Методы статистического анализа в управлении. Учеб. пособие — М.: Дело, 2002. — 520 с.
6. Шиндовский Э., Шюрц О. Статистические методы управления качеством. Контрольные карты и планы контроля. / Пер. с нем. В. М. Ивановой и И. О. Решетниковой. — М.: Мир, 1976. — 597 с.