Оценка своих профессиональных компетенций будущими учителями математики



В статье предпринята попытка выявить, как будущие учителя математики оценивают свою профессиональную подготовку и насколько у них развиты умения самооценки.

Ключевые слова: профессиональные компетенции, профессиональный стандарт педагога, самооценка.

Требования к знаниям и умениям будущих учителей математики определяются федеральным государственным образовательным стандартом высшего образования 3++ по направлению Педагогическое образование [6] и Профессиональным стандартом педагога [1].

Целью исследования было выяснить, как сами студенты оценивают соответствие своей подготовки Профессиональному стандарту педагога.

В соответствии с требованиями модуля «Математика» Профессионального стандарта педагога нами был составлен Google-опросник, в котором студентам необходимо было указать свой уровень по каждому профессиональному качеству (высокий, средний или низкий). Перечень вопросов представлен ниже.

1. Оцените уровень своих знаний основ математической теории и перспективных направлений математики.
2. Оцените уровень своих знаний теории и методики преподавания математики.
3. Оцените свое умение формировать конкретные знания, умения и навыки в области математики у обучающихся.
4. Оцените свой навык ведения диалога с обучающимися или группой обучающихся в процессе решения задачи, выявления сомнительных мест, подтверждения правильности решения.
5. Оцените свой уровень умения решения задач элементарной математики.
6. Оцените свой уровень владения основными математическими компьютерными инструментами: визуализация данных, зависимость, отношения, процессы, геометрические объекты, вычисления, обработка данных.
7. Оцените свое умение совместно с учащимися проводить анализ учебных и жизненных ситуаций, в которых можно применить математический аппарат и математические инструменты.
8. Оцените свое умение в организации исследования — эксперимента, к обнаружению закономерностей.
9. Оцените свое умение совместно с обучающимися применять методы и приемы понимания математического текста, его анализа, структуризации, реорганизации, трансформации.
10. Оцените свое умение совместно с обучающимися строить логические рассуждения в математических и иных контекстах, понимать рассуждение обучающихся.
11. Оцените свое умение обеспечивать коммуникативную и учебную «включенность» всех учащихся в образовательный процесс.
12. Оцените свое умение в поддержании высокой мотивации и развития способностей учащихся к занятиям математикой.
13. Оцените свое умение обеспечивать помощь обучающимся, не освоившим необходимый материал, в форме предложения специальных заданий, индивидуальных консультаций.

В опросе приняли участие 49 студентов 3–5 курсов профиля Математика. Информатика Южно-Уральского государственного гуманитарно-педагогического университета.

Высокие оценки студенты дали своим умениям ведения диалога с обучающимися или группой обучающихся в процессе решения задачи, выявления сомнительных мест, подтверждения правильности решения, решения задач элементарной математики, совместно с обучающимися строить логические рассуждения в математических и иных контекстах, понимать рассуждение обучающихся, обеспечивать помощь обучающимся, не освоившим необходимый материал, в форме предложения специальных заданий, индивидуальных консультаций.

С целью выявить внутреннюю согласованность ответов студентов мы сравнили распределения ответов по уровням для близких по содержанию вопросов с помощью критерия Пирсона [2].

Сравним распределения ответов на 4 и 10 вопросы. По результатам опроса мы имеем следующие данные (табл. 1).

Таблица 1

Сопоставление распределений ответов на 4 и 10 вопросы по уровням сформированности умений

Уровень	Высокий		Средний		Низкий
Вопрос	%	Кол-во чел	%	Кол-во чел	%	Кол-во чел
Оцените свой навык ведения диалога с обучающимися или группой обучающихся в процессе решения задачи, выявления сомнительных мест, подтверждения правильности решения	46,9	23	42,9	21	10,2	5
Оцените свое умение совместно с обучающимися строить логические рассуждения в математических и иных контекстах, понимать рассуждение обучающихся	46,9	23	46,9	23	6,1	3

Значение критерия Пирсона оказалось равным 0,591. Число степеней свободы равно 2 (уровней три), поэтому Поскольку , можно сделать вывод, что распределения достоверно не отличаются и ответы на эти вопросы согласованны.

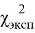
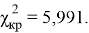
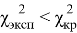
Сравним ответы на 2 и 10 вопросы. По результатам опроса мы имеем следующие данные (табл. 2).

Таблица 2

Сопоставление распределений ответов на 2 и 10 вопросы по уровням сформированности умений

Уровень	Высокий		Средний		Низкий
Вопрос	%	Кол-во чел	%	Кол-во чел	%	Кол-во чел
Оцените уровень своих знаний теории и методики преподавания математики	20,4	10	74,1	35	8,2	4
Оцените свое умение совместно с обучающимися строить логические рассуждения в математических и иных контекстах, понимать рассуждение обучающихся	46,9	23	46,9	23	6,1	3

Сравнение этих распределений дало значение критерия Пирсона =7,747. Таким образом, . Несмотря на то, что, по нашему мнению, знание теории и методики обучения математике взаимосвязано с умением понимать рассуждение обучающихся и совместно с ними строить логические рассуждения, получилось существенно различие в распределениях. Мы связываем это с тем, что студенты недооценивают необходимость знаний методики обучения математике для ее успешного преподавания, а также с тем, что студенты переоценивают свои педагогические умения.

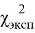
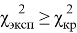
Сформированность умения совместно с учащимися проводить анализ учебных и жизненных ситуаций, в которых можно применить математический аппарат и математические инструменты, умения в поддержании высокой мотивации и развития способностей учащихся к занятиям математикой и владения основными математическими компьютерными инструментами визуализации данных, зависимостей, отношений, процессов, геометрических объектов, вычислений и обработки данных многие студенты оценили низко. Это означает, что студенты ощущают недостаточность своих знаний и умений. Этот вывод обращен к преподавателям: необходимо искать пути и средства более эффективного обучения студентов как владению компьютерными инструментами, так и продуктивному общению с учащимися при решении задач.

С целью проверки умений самооценки профессиональных компетенций будущих учителей математики мы сопоставили результаты самооценки студентов и оценки этих же качеств студентов преподавателями с помощью такого же Google-опросника (рис. 1). В опросе участвовало 7 преподавателей математических дисциплин.

Рис. 1. Опросник для преподавателей

Заметим, что оценка преподавателей ни в одном вопросе не превышала собственную оценку студентов. При подсчете критерия Пирсона для сравнения распределений оценок студентов и преподавателей умений совместно с учащимися проводить анализ учебных и жизненных ситуаций, в которых можно применить математический аппарат и математические инструменты, совместно с обучающимися строить логические рассуждения в математических и иных контекстах, понимать рассуждение обучающихся, знаний основ математической теории и перспективных направлений математики и навыка ведения диалога с обучающимися или группой обучающихся в процессе решения задачи, выявления сомнительных мест, подтверждения правильности решения существенных различий выявлено не было. Можно сделать вывод, что студенты реалистично оценивают свои компетенции в данных вопросах.

В результате проверки выяснилось, что оценка студентами и преподавателями умений формировать конкретные знания, умения и навыки обучающихся в области математики, совместно с обучающимися применять методы и приемы понимания математического текста, его анализа, структуризации, реорганизации, трансформации существенно различается. Преподаватели оценили именно эти умения студентов ниже, чем сами студенты. Это согласуется с ранее проведенными исследованиями [3; 4; 5]. Для улучшения данных умений студентам необходимо уделить особое внимание методике формирования конкретных знаний, умений и навыков в области математики у учеников, научиться совместной работе с учащимися в построении логических рассуждений в математических контекстах, а также работать над своим умением самооценки.

Статья выполнена при финансовой поддержке ФГБОУ ВО «МГПУ им. М. Е. Евсевьева» по договору на выполнение научно-исследовательских работ от 27.07.2021 г. № 16–618 по теме «Мониторинг формирования профессиональных компетенций будущих учителей математики в условиях реализации профессионального стандарта педагога».

Литература:

1. Профессиональный стандарт. Педагог (педагогическая деятельность в дошкольном, начальном общем, основном общем, среднем общем образовании). Утвержден приказом Министерства труда и социальной защиты Российской Федерации от 18 октября 2013 г. № 544н, г. Москва. Available at: http://www.rg.ru/2013/12/18/pedagog-dok.html
2. Суховиенко Е. А. Математическая модель рейтинговой системы диагностики компетенций будущих учителей математики. Актуальные проблемы развития среднего и высшего образования. Межвузовский сборник научных трудов. — Челябинск: КрайРА, 2015.
3. Суховиенко, Е. А. Диагностика профессиональных компетенций магистрантов в свете реализации профессионального стандарта педагога // Мир науки, культуры, образования. — 2016. — № 6 (61).
4. Суховиенко, Е. А. Диагностика соответствия подготовки будущих учителей математики профессиональному стандарту педагога // Мир науки, культуры, образования. — 2018. — № 3 (70).
5. Суховиенко, Е. А. Мониторинг формирования проектных умений будущих педагогов в период педагогической практики / Е. А. Суховиенко, С. А. Севостьянова, Р. М. Нигматулин, Е. В. Мартынова // Современные проблемы науки и образования. — 2020. — № 6. — С. 75.
6. ФГОС ВО (3++) по направлению 44.03.05 «Педагогическое образование» [Электрон. ресурс] // Портал Федеральных государственных образовательных стандартов высшего образования. Режим доступа: http://fgosvo.ru/uploadfiles/FGOS %20VO %203++/Bak/440305_B_3_16032018.pdf (дата обращения: 12.09.2021).