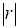В статье излагается опыт использования средств Excel для установления корреляционных зависимостей между исследуемыми величинами в автоматическом режиме. Показаны преимущества этих средств перед ручным счетом в точности и трудоемкости при выполнении многовариантных расчетов корреляционно-регрессионного анализа.
Ключевые слова: корреляция, регрессия, коэффициент корреляции, поле корреляции, Excel.
Связи между реальными явлениями в природе сложны и многообразны, однако их можно определенным образом классифицировать. В технике и естествознании часто речь идет о функциональной зависимости между переменными х и у , когда каждому возможному значению х поставлено в однозначное соответствие определенное значение у . Это может быть, например, зависимость между током и величиной сопротивления в электрической цепи (закон Ома).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из которых ничтожно мало, а число их велико. В этом случае связь теряет свою однозначность, а изучаемая физическая система переходит не в определенное состояние, а в одно из возможных для нее состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения.
В 1886 году английский естествоиспытатель Френсис Гальтон для обозначения характера подобного рода взаимодействий ввёл термин «корреляция». Позже его ученик Карл Пирсон разработал математическую формулу, позволяющую дать количественную оценку корреляционным связям признаков.
Следует отметить, что коэффициент корреляции Пирсона можно применять только при соблюдении следующих условий:
– Обе переменные являются количественными и непрерывными.
– Как минимум один из признаков (а лучше оба) имеет нормальное распределение (поэтому расчет этого коэффициента является параметрическим методом оценки взаимосвязи признаков).
– Зависимость между переменными носит линейный характер.
– Гомоскедастичность (вариабельность одной переменной не зависит от значений другой переменной).
– Независимость участников исследования друг от друга (признаки Х и Y у одного участника исследования независимы от признаков Х и Y у другого).
– Парность наблюдений (признак Х и признак Y изучаются у одних и тех же участников исследования).
– Необходим достаточно большой объем выборки, как минимум 25 наблюдений.
– Для адекватной проекции расчетов на генеральную совокупность выборка должна быть репрезентативной.
Таким образом, все эти условия оказывают влияние на точность проведения корреляционного анализа. Далее мы рассмотрим их более подробно.
Корреляционный анализ решает две основные задачи:
– Первая задача заключается в определении формы связи, т. е. в установлении математической формы, в которой выражается данная связь. Это очень важно, так как от правильного выбора формы связи зависит конечный результат изучения взаимосвязи между признаками.
– Вторая задача состоит в измерении тесноты, т. е. меры связи между признаками с целью установить степень влияния данного фактора на результат. Она решается математически путем определения параметров корреляционного уравнения.
Затем проводятся оценка и анализ полученных результатов при помощи специальных показателей корреляционного метода (коэффициентов детерминации, линейной и множественной корреляции и т. д.), а также проверка существенности связи между изучаемыми признаками.
Для количественной оценки тесноты связи служит выборочный коэффициент корреляции.
Коэффициент корреляции r вычисляется по значениям функций отклика в области эксперимента [1, с. 94]:

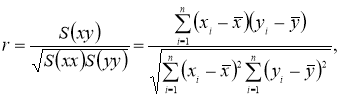
где x i , y i — каждое текущее значение функции в области эксперимента;
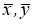
Величины ковариации S(xy) — переменной х от переменной у определяется по формуле (2):
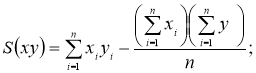
ковариации S(xx) — переменной х от переменной х определяется по формуле (3):
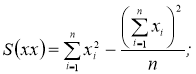
ковариации S(уу) — переменной у от переменной у определяется по формуле (4):
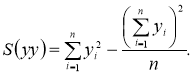
Если функции зависят от одного аргумента, то, проведя корреляционный анализ, можно установить взаимный рост или убывание функций друг от друга в зависимости от изменения аргумента.
О наличии или отсутствии корреляции между двумя случайными величинами качественно можно судить по виду поля корреляции, поместив экспериментальные точки на координатную плоскость. Положительная корреляция между случайными величинами представлена на рис. 1, а обратная корреляция — на рис. 2. Сравнительно слабая корреляция представлена на рис. 3, на рис. 4 приведен пример отсутствия корреляции.
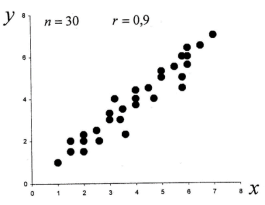
Рис. 1. Корреляция линейная, рост одной функции приводит к увеличению другой. r > 0, r = 0,9.
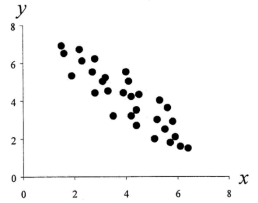
Рис. 2. Корреляция обратно линейна, рост одной функции приводит к снижению другой. r < 0, r= -0,9
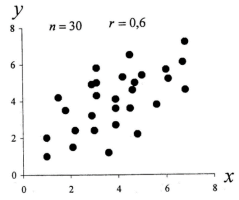
Рис. 3. Слабая корреляция, r = 0,6
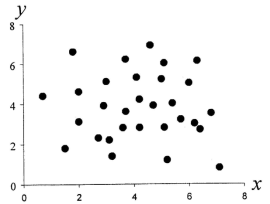
Рис. 4. Корреляция отсутствует, r = 0
Для независимых случайных величин коэффициент корреляции равен нулю, но он может быть равен нулю для некоторых зависимых величин, которые при этом называются некоррелированными. Для случайных величин, имеющих нормальное распределение, отсутствие корреляции означает и отсутствие всякой зависимости.
Коэффициент корреляции характеризует степень тесноты линейной зависимости. В общем случае, когда величины X и Y связаны произвольной стохастической зависимостью, коэффициент корреляции может иметь значение в пределах -1 ≤ r ≤ +1.
|
Диапазон значений
|
Линейная корреляционная зависимость Y от X |
|
0–0,1 |
практически отсутствует |
|
0,1–0,3 |
слабая |
|
0,3–0,5 |
умеренная |
|
0,5–0,7 |
заметная |
|
0,7–0,9 |
сильная |
|
0,9–0,99 |
очень сильная |
|
0,99–1 |
практически функциональная |
По сути, коэффициент корреляции означает степень, в которой две переменные движутся в тандеме друг с другом. Положительный коэффициент, вплоть до максимального уровня 1, указывает, что движения двух переменных идеально выровнены и в одном направлении — если одна увеличивается, другая увеличивается на ту же величину. Отрицательный коэффициент, вплоть до минимального уровня -1, является прямо противоположным, указывая на то, что две величины движутся в противоположном направлении друг относительно друга. Естественно, почти все реальные явления находятся где-то посередине между этими двумя крайностями.
При интерпретации результатов корреляционного анализа нужно иметь в виду, что коэффициент корреляции — статистический показатель. Он не содержит предположения, что изучаемые величины находятся в причинно-следственной связи. Поэтому любая трактовка корреляционной зависимости должна основываться на предварительной информации.
После обнаружения стохастических связей между изучаемыми переменными величинами исследователь приступает к математическому описанию интересующих его зависимостей. Другими словами, необходимо перейти от корреляционного анализа к регрессионному анализу.
При применении специальных программных продуктов для корреляционного анализа можно воспользоваться встроенными функциями.
1 способ — Расчет в Microsoft Office Excel 2007/2010/2016 (самый простой способ).
При расчете в Excel применяют встроенную функцию КОРРЕЛ(массив1; массив2) (рис. 5).
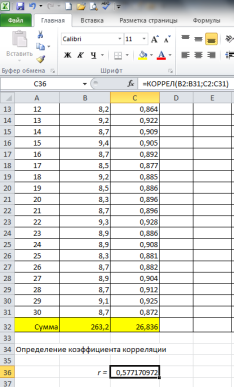
Рис. 5. Расчет коэффициента корреляции в EXCEL
2 способ — Расчет в программе «Корреляционный анализ».
По мере ввода данных можно посмотреть графическую интерпретацию экспериментальных данных, для этого используют функцию «Вставка» — «Диаграммы» — «Точечная».
Перед расчетом необходимо визуально оценить полученные кривые и ответить на вопрос: коррелируют ли полученные зависимости; после этого программа произведет расчет коэффициента корреляции и делается вывод о существовании корреляционной зависимости для данных кривых.
3 способ — Расчеты в создаваемых шаблонах с расширением имеющихся возможностей Excel.
Для более детального расчета коэффициента корреляции авторами был предложен шаблон Excel в виде расчетной таблицы, содержание ячеек которой представлено на рисунке 6. Метод расчета был принят в соответствии с источником [1, c. 96].
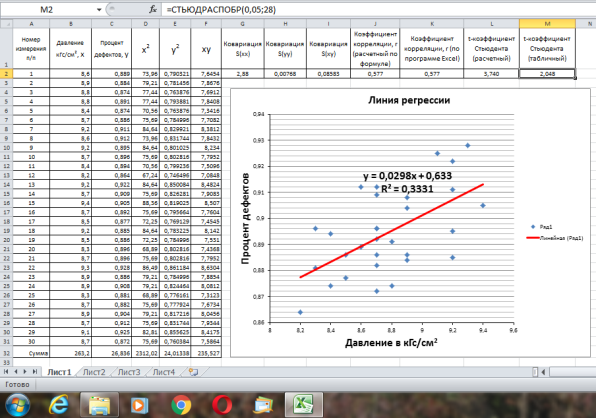
Рис. 6. Определение коэффициента корреляции с расчетом промежуточных величин и графической интерпретацией данных
В качестве объекта исследования был рассмотрен пример, заключавшийся в том, что фирма-производитель пластиковых емкостей, изготавливаемых методом литья под давлением, сталкивается с трудностями из-за дефектных емкостей, имеющих слишком тонкие стенки. Было высказано предположение, что причина неподходящей толщины стенок заключается в вариации давления сжатого воздуха, которое каждый день меняется. В таблице (см. рис. 6) приведены данные о давлении воздуха и проценте дефектов. Требуется найти коэффициент корреляции, устанавливающий связь между давлением воздуха и процентом дефектов пластиковых емкостей.
На практике коэффициент корреляции
ρ
обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции
r
. Произвести точечную оценку коэффициента корреляции
r
по
t
-критерию Стьюдента
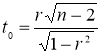
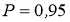
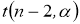
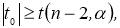
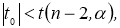
Точечная оценка t -критерия коэффициента корреляции r для рассмотренного примера по предложенной формуле дала значение t 0 = 3,740> t 28, 0,95 = 2,048, что позволяет отбросить нулевую гипотезу, т. е., признать существенность значения коэффициента корреляции. Критическое значение t- критерия находилось с помощью функции Excel по формуле: СТЬЮДРАСПОБР (критерий значимости, число степеней свободы).
Для подтверждения корректности предложенного расчета с помощью средств Excel был произведен повторный расчет тех же исходных данных с использованием классических формул, изложенных в [2, с. 228–229].
Окончательные расчеты подтвердили полную сходимость значений линейного коэффициента корреляции ( r = 0,577) и коэффициентов уравнения регрессии: а = 0,0298 и b = 0,633 (рис. 7 и рис. 8), полученных разными способами: с помощью шаблона, предложенного авторами, и метода с использованием классических формул математической статистики.
![Схема расчета в Excel коэффициента корреляции с использованием формул математической статистики [2, с. 234]](https://moluch.ru/blmcbn/85284/85284.019.png)
Рис. 7. Схема расчета в Excel коэффициента корреляции с использованием формул математической статистики [2, с. 234]
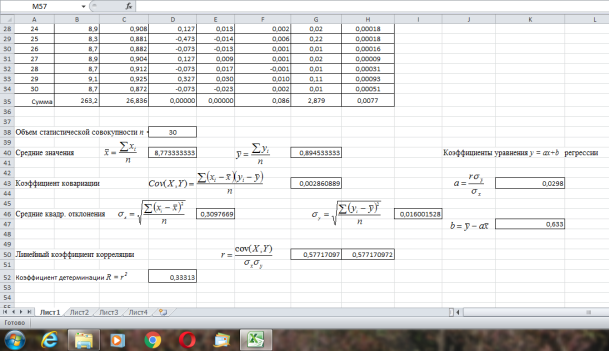
Рис. 8. Окончательные данные повторного расчета коэффициента корреляции
Графическая интерпретация данных расчета также подтвердила полное совпадение уравнений и линий регрессии.
Если коэффициент корреляции значим, то коэффициенты регрессии в уравнениях также значимо отличаются от нуля, а интервальные оценки в случае малых выборок ( n < 30) для них можно получить по следующим формулам [2, с. 236]:
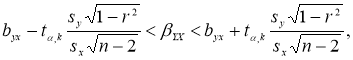
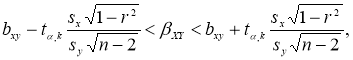
где
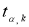
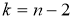
В случае больших выборок (
n
≥ 30)
t
-распределение заменяется на Z-распределение стандартного нормального распределения с
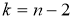
Выводы
1. Расчет показателей корреляционного и регрессионного анализа сопровождается большим количеством громоздких формул и значительным объемом вычислительной работы, проведение которой без использования компьютера практически невозможно при выполнении реальных многовариантных статистических расчетов корреляционно-регрессионного анализа и статистического прогнозирования.
2. В настоящее время разработано достаточное количество универсальных и специализированных программ статистического анализа данных. Сложность проведения расчетов и стала предметом актуальности данной работы, вследствие чего было приведено в пример удобное программное средство Excel, позволяющее успешно решать ряд задач указанного характера.
3. Используя MS Excel можно построить в автоматическом режиме диаграмму разброса. Она представит связь между изучаемыми факторами корреляционного анализа и результативным признаком, а также позволит определить степень корреляции без процесса построения поля корреляции при ручном счете, который занимает значительное количество времени при больших объемах выборки.
4. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения параметров качества продукции, приводящие к выпуску дефектных изделий.
Литература:
1. Статистические методы повышения качества: Пер. с англ./ Под ред. Хитоси Кумэ. — М.: Финансы и статистика, 1990. — 304 с.
2. Математическая статистика: Учебник / Иванова В. М., Калинина В. Н., Нешумова Л. А. и др. — М.: Высшая школа, 1981–371 с.
3. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
4. Сулицкий В. Н. Методы статистического анализа в управлении. Учеб. пособие — М.: Дело, 2002. — 520 с.