В 1965 г. Д. Слепян предложил концепцию перестановочной модуляции [1]. Передача информации в схемах с перестановочной модуляцией осуществляются путем перестановки порядка набора символов. В оригинальной перестановочной модуляции кодовое слово s (1) = R Mx 1 определяется формулой:
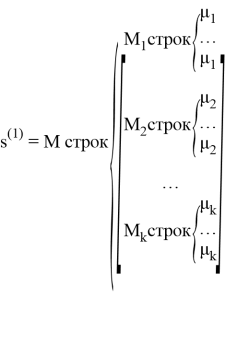
где у нас есть целое число
M=M
1
+M
2
+…+M
k
и вещественное число значения
µ
1
< µ
2
<
В уравнении (1), µ 1 повторяется M 1 раз. Затем другие кодовые слова генерируются путем перестановки чисел s (1) . Мощность множества возможных кодовых слов N c рассчитывается по формуле 2:
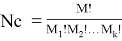
Мощность множества возможных кодовых слов увеличивается с факториальным порядком.
Фазово-импульсная модуляция и импульсно-кодовая модуляция являются частными случаями перестановочной модуляции. В частности, в фазово-импульсной модуляции кодовые слова генерируются следующим исходным кодовым словом:
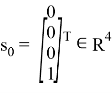
где символам из матрицы {0;0;0} соответствует значение M 1 =3, а символу {1} соответствует значение М 2 =1. Следовательно, M=M 1 +M 2 =4 и
(µ 1 ; µ 2 ) = (0; 1).
Nc=M!/(M 1 !×M 2 !)=4!/(3!×1!)=4. (4)
Основываясь на формуле 4, благодаря перестановке четырех чисел можно сгенерировать следующие кодовые слова:
s (1) = [0 0 0 1] Т ; s (2) = [0 0 1 0] Т ;
s (3) = [0 1 0 0] Т ; s (4) = [1 0 0 0] T . (5)
Кодовые слова в формуле (5) также соответствуют и кодовым словам в схеме пространственной модуляции, в которой используется только одна из нескольких антенн в определенный момент времени передачи. Аналогичным образом хорошо известная схема фазово-импульсной кодирует входные биты временной позицией импульса. Таким образом, схема пространственной модуляции — это пространственный аналог схемы фазово-импульсной модуляции, которая отображает информационные биты во временной области.
Разберем еще один пример. В формуле 6 описывается начальное кодовое слово:
a
1
= [1;2]
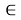
Тогда мощность возможных кодовых слов рассчитывается по формуле:
Nc=2!/(1!*1!)=2. (7)
Исходя из формулы 7 два кодовых слова перестановочной модуляции задаются формулами a 1 = [1;2] и a 2 = [2;1]. Предположим, что мы отображаем векторы a 1 и a 2 на пространственно-временной матрице, после чего задаем примерный набор кодовых слов:
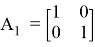
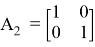
В линейной алгебре каждая матрица из формулы (8) называется перестановочной матрицей. Из формулы 8 можно показать, что перестановочные матрицы являются базисом STBC-модуляции, основанной на пространственной модуляции, и ее дифференциального аналога.
Гибридная перестановочная модуляция : классическая схема перестановочной модуляции конвертирует входные биты в перестановочные последовательности, тогда как гибридная схема перестановочной модуляции делит биты на входе на две части [2]. В данном случае первые биты используются для выбора набора частот, пока остальные биты используются для генерации символов стандартной амплитудной и фазовой манипуляции, которые переносятся выбранными частотами [3].
В отличие от распространенных схем модуляции, гибридная схема перестановочной модуляции отображает предоставленную последовательность в частотной области, по аналогии с классической концепцией перестановочной модуляции. Если отобразить перестановочную последовательность в частотной области, гибридная схема перестановочной модуляции становится эквивалентна обобщенной пространственной модуляции (GSM), которая представляет собой когерентную МIMO-схему [4].
В этой статье концепция перестановочной модуляции интерпретируется в обобщенном виде. Существует большое разнообразие схем перестановочной модуляции, благодаря которым передаются дополнительные биты за счет выбора расширяющей последовательности, индекса поднесущей, передающей антенны, дисперсионной и перестановочной матрицы. Эти схемы обычно основываются на базовой перестановке структуры. Поэтому допустимо относить эти схемы к перестановочной модуляции.
Произвольную модуляцию можно отнести к перестановочной, если в ее основе лежит следующая комбинационная матрица:
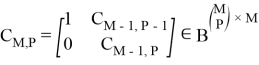
где из множества M выбирается P произвольных элементов, 0 — это нулевой вектор длины
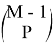
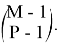
Таким образом, матрица в формуле 9 отражает состояние включения-выключения произвольных элементов, таких как передающие антенны или индексы поднесущих. Например, если мы рассмотрим случай
(M; P) = (4; 1), то комбинационная матрица принимает следующий вид [5]:
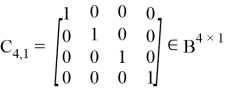
где каждая строка соответствует заданным кодовым словам SSK, представленных в формуле (5). Кроме того, для случая (M; P) = (4; 2) комбинированная матрица имеет следующий вид:
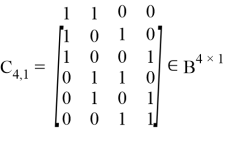
где каждая строка соответствует кодовым словам перестановочной модуляции, произведенных от последовательности s (1) = [0 0 1 1] T , т. е.
(M1; M2) = (2; 2).
Поскольку количество кодовых слов в перестановочной модуляции увеличивается с ростом факториального порядка, как указано в формуле 2, перестановочная модуляция была применена к носителям хранения данных для увеличения емкости.
Например, перестановочная модуляция и ее разновидности применяются для стеганографии, объемной голографической памяти, флеш-памяти и для твердотельных хранилищ.
Независимо от концепции перестановочной модуляции в 1991 г. была предложена иная концепция модуляции для расширения спектра [6].
В основанном на перестановочной модуляции способе расширения спектра осуществляется выборка P из M последовательностей перестройки. Такой способ называют методом расширения спектра посредством параллельной комбинаторики . К этой концепции можно отнести обычную связь с расширенным спектром, где выбирается только P = 1 из M последовательностей.
На основе концепции параллельной комбинаторики, была предложена схема OFDM-модуляции с ее использованием, где из набора поднесущих выбирается конкретная комбинация. Поскольку набор комбинаций поднесущих соответствует комбинационной матрице из формулы 9, то такая схема рассматривается как один из видов перестановочной модуляции. Концепция параллельной комбинаторики была исследована в контексте широкополосных беспроводных сетей.
С 2009 года схема OFDM с перестановочной модуляцией стала привлекать научный интерес, потому что данный вид модуляции улучшает как частотное разнесение, так и выигрыш от кодирования по сравнению с обычной OFDM-модуляцией. В 2015 году была предложена модуляция с переменным полиномом перестройки частоты, которую можно отнести к виду перестановочной модуляции. [7]
Литература:
1 D. Slepian, “Permutation modulation,” Proceedings of the IEEE, vol. 53, no. 3, стр. 228–236, 1965.
2 W. Li, Study of hybrid permutation frequency phase modulation. Master Thesis, University of Ottawa, 1996.
3 A. Yongacoglu и W. Li, “Hybrid permutation frequency phase modulation,” in IEEE Canadian Conference on Electrical and Computer.
4 J. Jeganathan, A. Ghrayeb, и L. Szczecinski, “Generalized space shift keying modulation for MIMO channels,” in IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Cannes, France, Sept. 15–18, 2008.
5 P. K. Frenger и N. A. B. Svensson, “Parallel combinatory OFDM signaling,” IEEE Transactions on Communications, vol. 47, no. 4, pp. 558–567, 1999.
6 S. Sasaki, J. Zhu, и G. Marubayashi, “Performance of parallel combinatory spread spectrum multiple access communication systems,” in IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, Sept. 23–25, 1991.
7 G. Kaddoum, Y. Nijsure, and H. Tran, “Generalized code index modulation technique for high-data-rate communication systems,” IEEE Transactions on Vehicular Technology, vol. 65, no. 9, pp. 7000–7009, 2016.







