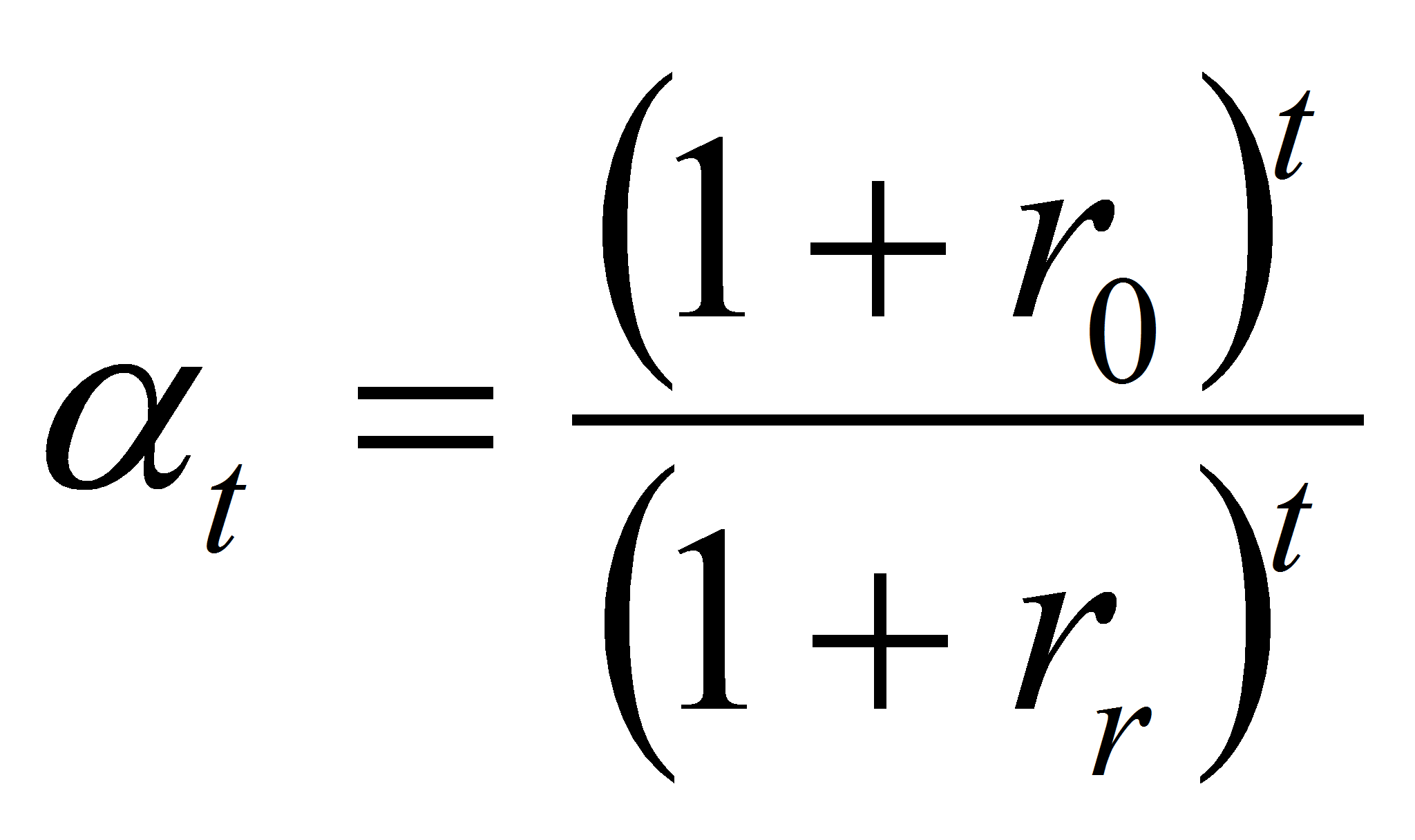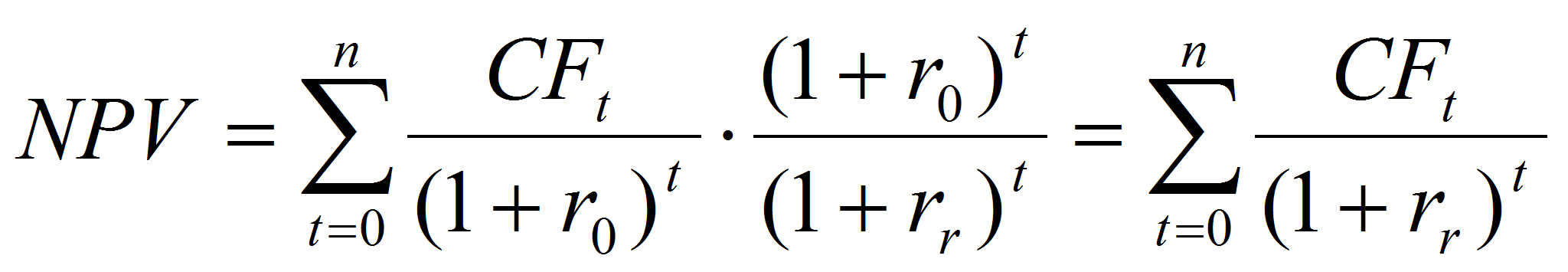Оценка риска при определении современной стоимости денежных потоков

Традиционным подходом при проведении оценки современной стоимости будущих поступлений денежных средств выступает модель дисконтирования денежного потока (Discounted Cash Flows Model), которая представляет собой приведение ожидаемых поступлений денежных средств к текущему моменту времени на основе метода математического дисконтирования [5, с. 25]:

где FV - сумма денежных средств, ожидаемая к получению в будущем, руб.; PV-современная стоимость денежных средств, d - ставка дисконта, %; t - период планирования, лет.

Предложенная на этой основе DCF-модель имеет вид[2, с. 57]::

где CF_t – величина денежного потока в периоде t, руб.

Ставка дисконтирования, принятая в данной модели, отражает влияние на денежный поток четырех факторов:

-оборачиваемости активов предприятия;

-риска денежного потока;

-ожидаемой доходности вложений;

-инфляции.

Таким образом, инфляционные процессы, происходящие в стране реализации инвестиции, влияют на уровень ставки дисконта, определяя ее минимальное значение. Если предположить, что инфляция отсутствует, риск утраты ожидаемой доходности минимален, т.е. стремится к нулю, тогда будущие поступления дисконтируются по ставке дисконта, равной требуемой инвесторами доходности вложений.

Рассмотрим методику включения риска в расчет современной стоимости будущих денежных потоков более подробно. Известно, что риски проекта увеличиваются со временем. Поэтому денежный поток через три года будет намного более рискованным, чем денежный поток через один год. Денежный поток через десять лет будет еще более рискованным. Сложность оценки заключается в том, насколько именно возрастает риск с течением времени реализации проекта. И здесь может быть использовано два метода включения риска в анализ [3 ,с.375]:

1. метод безрисковых эквивалентов (Certainty Approach Equivalent, СЕ);

2. метод скорректированной на риск ставки дисконта (Risk-Adjusted Discount Rate, RADR).

В общепринятой модели дисконтирования денежных потоков, когда риск будущих поступлений учитывается путем увеличения ставки дисконта на величину премии за риск (RADR, скорректированная на риск ставка дисконта), возрастание риска во времени осуществляется по одной и той же схеме:

где CF_t – размер денежного потока за период t, руб.; RADR – уровень риска, %; r₀- безрисковая ставка, %; n – количество периодов, по которым возникают денежные потоки.

Ставка дисконтирования, используемая в DCF–model, должна включать в себя две составляющие. Первая составляющая - безрисковая ставка процента, которая может быть рассчитана как ставка рефинансирования ЦБ РФ (8%) или как средняя ставка доходности по государственным ценным бумагам (5-6%) за определенный период. Вторая составляющая - премия за риск, которая может варьироваться от 3% до 20% в зависимости от уровня риска. Риск денежного потока учитывается в модели путем увеличения ставки дисконта: чем выше риск, тем выше будет ставка дисконта. Например, согласно Методическим рекомендациям по оценке эффективности инвестиционных проектов, при низком уровне риска величина поправки на риск колеблется в диапазоне от 3 до 5 %, при высоком может достигать 20% (таблица 1). [4 ,с. 154]

Включение риска в анализ по схеме RADR называется компаундированием риска. Несмотря на фундаментальность данной модели, нет четких доказательств того, что риск всегда возрастает именно по этой экспоненциальной функции. Кроме того, данная модель содержит допущения о постоянном темпе возрастания риска во времени, что также является спорным моментом. Также не доказано, что компаундирование отражает наиболее типичную схему возрастания риска.

Все вышеизложенное дает возможность исследовать этот процесс более детально, что подразумевает под собой необходимость обращаться к более гибким моделям, которые позволяют задавать произвольный график изменения риска во времени.

Таблица 1

Величина поправки на риск

Рассматривая метод безрисковых эквивалентов, специалисты отмечают его большую применимость на практике при оценке риска будущих поступлений инвестиционного проекта, поскольку в оценку вводится коэффициент корректировки неопределенности, который учитывает повышенный риск проекта по отношению к среднему риску инвестирования в стране. Поскольку определенный уровень риска существует всегда, то можно полагать, что корректировка на риск необходима только в случае наличия повышенного риска, т.е. когда уровень риска данной инвестиции выше, чем альтернативного вложения денежных средств. Модель дисконтирования денежного потока в этом случае принимает вид:

,

=>

где α_t – коэффициент корректировки неопределённости в период t; r_r - уровень риска инвестиции, %.

Если рассмотреть, как изменяется стоимость будущих поступлений денежных средств при возрастании риска и периода инвестирования (таблица 2), то можно заметить, что при включении риска в анализ по методу безрисковых эквивалентов в случае, если уровень риска проекта минимален (ниже уровня безрисковой ставки), множитель дисконтирования будет равен единице независимо от горизонта планирования. В то же время при оценке этого же денежного потока по методу скорректированной на риск ставки дисконта, величина ожидаемых поступлений будет скорректирована уже в первый период.

Таблица 2

Сравнительная таблица множителей дисконтирования при различных уровнях риска и периода планирования(r₀=5%)

Также нетрудно заметить, что использование механизма RADR большими темпами снижает ожидаемую величину денежного потока. Это приводит к тому, что при повышенном уровне риска даже на сравнительно небольшом временном периоде планирования от ожидаемых поступлений остается менее 50%, а для долгосрочного планирования делает оценку практически бессмысленной, т.к. снижение приведенной стоимости приближается к 100%. При этом существенные различия между двумя методами наблюдаются только при невысоком или среднем риске, при повышенном риске на долговременном горизонте планирования различия слабо заметны. Так, при поправке на риск в 3% в двадцатом периоде различие составляет 0,404, в то время как при уровне риска 15% уже 0,043.

Таким образом, оценка будущих денежных поступлений по методу безрисковых эквивалентов является более приемлемой при оценке денежных потоков, поскольку дает возможность оценивать однократные рисковые денежные потоки в начальный момент оценки, а также учитывает возможность изменения уровня риска в период реализации проекта. Достоинством применения этого метода является простая реализация и совмещение с любыми способами оценки премии за риск денежных потоков, в которых риск выражается их стандартным отклонением для соответствующего периода времени. Метод безрисковых эквивалентов представляет большую гибкость в сравнении с методом скорректированной на риск ставки дисконта, при котором риск возрастает во времени по схеме компаундирования процентов, независимо от характера и типа денежных выплат.

Для обоснования ставки дисконта, отражающей поправку на риск, можно использовать методы математической статистики. В случае, если величина риска подвержена значительным колебаниям при разных сценариях развития событий (оптимистичный, вероятный, пессимистичный) риск может быть выражен как стандартное отклонение. Если предположить, что значения риска денежного потока являются случайными величинами, распределенными по нормальному (гауссовскому) закону, то величина поправки на большую рискованность (r_r) может измеряться как средневзвешенное отклонение случайной величины от ее математического ожидания. Функция изменения риска в простейшем случае может быть описана стандартным отклонением:

г
де p_i – вероятность наступления событий по одному из сценариев, к-т; r_i – величина риска по i-му сценарию, %;r - среднее (ожидаемое значение) величины риска по i-му сценарию, %.

Простейший пример определения величины риска приведен в таблице 3.

Таблица 3

Изменение риска денежного потока при различных сценариях развития событий

Из таблицы следует, что если события будут развиваться так, как было запланировано, величина риска будет минимальна. Высокий уровень риска достигается в условиях неопределенности, когда вероятность развития каждого сценария одинакова и неопределенность наступления событий высока.

Литература:

1. Бригхэм Ю.Ф., Эрхардт М.С. Финансовый менеджмент: пер. с англ. Е.А. Дорофеевой. – М.: Питер, 2009. – 960 с.

2. Ковалев В.В. Управление финансовой структурой фирмы: учебн.-практ. пособие. – М.:ТК Велби, Изд-во Проспект, 2008. – 256 с.

3. Лукасевич И.Я. Финансовый менеджмент: учебник. – М.: Эксмо,2007. – 765 с.

4. Методические рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования: Утверждены Минэкономики РФ, Минфином РФ и Госстроем РФ от 21 июня 1999 г. N ВК 477.

5. Четыркин Е.М. Финансовая математика. – М.: Изд-во Дело,2000. – 345 с