Математическая модель работы шасси при демпфировании динамических воздействий в процессе взлета и посадки летательного аппарата

В настоящее время развитие авиации характеризуется тем, что от авиационной техники требуется неуклонное повышение эффективности эксплуатации. В связи с этим она становится все более дорогостоящей и специализированной. Эта тенденция требует от разработчиков минимизации запасов в расчетах не только прочности конструкции, но и показателей безопасности эксплуатации. От эксплуатационников требуется все более грамотная организация работы, обеспечивающая максимум эффективности при безусловном выполнении требований безопасности полетов. Таким образом, появляется настоятельная необходимость применения таких научно-технических методов, которые позволяют с малыми затратами получить как можно более точные характеристики движения ВС. Одним из таких методов является математическое моделирование.

Предлагаемый подход к решению этой проблемы включает в себя несколько принципиальных моментов[1].

1. Использование для анализа упругой работы планера конечно–элементных моделей.

2. Построение нелинейных математических моделей стоек шасси с использованием физических и конструктивных параметров стоек, что позволяет избежать значительного количества допущений при анализе.

3. Решение уравнений движения самолета в пространстве собственных форм колебаний планера дополненном пространством переменных интегрирования стоек. Это дает возможность, во-первых, учесть требуемое количество собственных форм для достижения необходимого приближения, а во-вторых, позволяет проводить расчет практически в реальном времени. В результате интегрирования уравнений определяются расчетные параметры в стойках и реакция планера в виде вкладов собственных форм. На следующем шаге вычисляются перемещения, скорости и ускорения точек упругой модели планера и эквивалентные статические нагрузки, как функции времени.

Особенность пространства переменных расчетной модели, отмеченная в последнем пункте, позволяет ввести термин – двухкомпонентная система. Первая компонента – линейная подсистема, описанная в ортогональном пространстве обобщенных переменных, и вторая – подсистема произвольных нелинейных элементов, заданная в пространстве физических переменных. Применение двухкомпонентных систем (ДКС) позволяет максимально корректно решать следующие задачи.

1. Анализ расчетных нагрузок на стойки шасси и конструкцию планера в случаях посадки.

2. Анализ расчетных нагрузок на стойки шасси и конструкцию планера в случаях пробега

по полосе с заданным профилем неровности, в том числе по грунтовой полосе.

3. Определение стояночных нагрузок на стойки как функции массы и центровки для самолетов с многостоечным шасси.

4. Проверка ограничений на расчетные параметры стоек, такие как работоемкость стойки, предельная нагрузка, предельный ход амортизатора и другие.

5. Оптимизация параметров амортизатора и опоры шасси по условию минимизации уровня нагрузок в конструкции планера при заданных ограничениях. Эти задачи возникают при расширении требований к самолету в процессе сертификации, а также при переходе на большие массы с сохранением прежних параметров стоек шасси. В некоторых случаях, как будет показано ниже, учет упругости планера позволяет снизить нагрузки со стороны шасси на планер и инерционные нагрузки на фюзеляже на 10–15%.

При проектировании новых самолетов предлагаемая методика позволяет оперативно просматривать большое количество схем шасси с тем, чтобы выбрать наиболее подходящую по уровню нагрузок.

Разумеется, интерес представляет задача проектирования стоек шасси, которая в данном случае может быть решена без создания неоправданных запасов сразу для требуемой предельной массы самолета.

Важным моментом применения математических моделей для определения нагрузок, является их верификация путем сравнения с летным экспериментом. В работе приводится ряд примеров моделирования летного эксперимента.

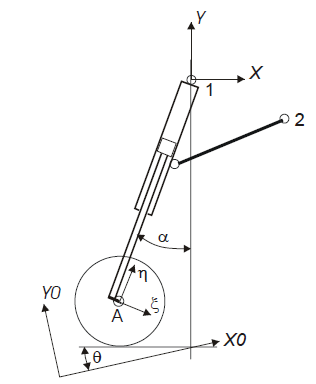
Амортизатор опоры шасси – однокамерный, плунжерного типа, с перетеканием жидкости через отверстие (рис.1).

Для разделения уравнений движения переменные интегрирования определяются в осях стойки [1]. В качестве переменных интегрирования выбирается вектор v = {,,ξ,η,ω}t .

Здесь ξ, η – перемещения оси колес в системе координат стойки, ω – угловая скорость вращения колес.

Перемещения узлов крепления стойки 1 и 2 используются:

- для определения расстояния от оси колес до опорной поверхности и вычисления обжатия пневматика δ_p, которое определяет кинематическое возбуждение стойки;

- для вычисления угла поворота местной системы координат (МСК) стойки α;

- для вычисления S и – обжатия и скорости обжатия амортизатора;

- для вычисления прогиба стойки δ.

Рисунок 1 - Амортизационная стойка самолета.

Поперечная жесткость стойки определяется нелинейной зависимостью
k_ξ = k_ξ (S).

Заданными параметрами являются:

m – масса подвижной части, ν – логарифмический декремент затухания,

p₀, V₀ – начальное давление и объем в газовой камере амортизатора,

f_op – площадь отверстия прямого хода, f_ok – площадь отверстий обратного хода, F_r – площадь штока, F_pl – площадь плунжера, F_ok – площадь камеры обратного хода, p_a – атмосферное давление, μ_b, μ_m – коэффициенты трения в буксах и манжетах, μ_k – коэффициент трения качения, r_k – радиус колес,

J_k – массовый момент инерции колес.

Дифференциальные уравнения записываются в виде [1]:

1. Ускорение движения точки A вдоль оси ξ:

= (T_ξ − (ν k_ξm / π) − k_ξδ)/m

2. Ускорение движения точки A вдоль оси η:

= (T_η −Q_a −Q_g −Q_f )/m

3. Уравнение раскрутки колес:

= (T_x0μ(r_k − δ_p ) −T_x0μ_k (r_k − δ_p / 3)) / J_k .

Здесь T_ξ иT_η – внешняя сила в проекции на оси стойки:

T_ξ = (T_y0 −mg) cos(θ + α) +T_x0 sin(θ + α)

T_η = −(T_y0 −mg)sin(θ + α) +T_x0 cos(θ + α)

Прогиб и относительная скорость в точке A:

δ = ξ − x₁ cosα

= − cosα

Реакция земли T₀ = {T_x0 ,T_y0} является функцией обжатия пневматика δ_p и коэффициентов трения проскальзывания μ_p:

T_y0 = T_y0(δ_p ) – функция обжатия пневматиков,

Компоненты реакции амортизатора:

Упругая сила, Q_a = ( p₁ − p_ath )F_r ,

Сила гидравлического сопротивления при перетекании жидкости через отверстие.

Сила гидравлического сопротивления на прямом ходе

Q_g = Δp_gF_pl,

ν₁ – скорость перетекания жидкости через отверстие прямого хода;

Сила трения в уплотнительных манжетах амортизатора и буксах:

здесь a и b – соответственно расстояния от оси колеса до нижней буксы и между буксами.

Компоненты реакции стойки на оси колеса в системе координат стойки:

P_ξ = k_ξδ или P_ξ = T_ξ-m

P_η = Q_a +Q_g +Q_f или P_η = T_η −m

Компоненты реакции стойки на оси колеса в системе координат самолета:

P_x = P_ξ cosα + P_η sinα

P_y = −P_ξ sin α + P_η cosα

Вектор реакций в узлах крепления стойки к фюзеляжу вычисляется в соответствии с уравнениями статического равновесия.

Для расчета эффективности по предложенной модели выполняется расчет носовой стойки тяжелого беспилотного самолета.

Записывается уравнение равновесия для стойки (сумма моментов относительно шарнира О₁ равна нулю):

;

Проекции силы S на оси координат X и Z равны:

кН.

Изгибающий момент М_x , действующий в плоскости ZOY , постоянен по длине стойки и равен величине:

кН∙м.

Изгибающий момент М_Y , действующий в плоскости XOY и в шарнире О₁ его значение равно нулю. В точках G и А значение М_Y равно:

кН∙м; кН∙м.

Сила S_Z приложена с эксцентриситетом:

кН∙м; кН∙м.

Стойка состоит из штока и цилиндра, связанных между собой буксами – силовая схема. Момент М_Y для штока равен нулю в точке С, а момент М_Y для цилиндра – нулю в точке D.

Крутящий момент равен: кН∙м.

Спроектированная с помощью математических моделей амортизационная стойка имеет большую энергоемкость, обеспечивая снижение амплитуды колебаний и динамических нагрузок передающихся на узлы крепления стойки к планеру самолета на 10–15%.

При проектировании новых самолетов предлагаемая методика позволяет оперативно просматривать большое количество схем шасси с тем, чтобы выбрать наиболее подходящую по уровню нагрузок.

Работа выполнена при финансовой поддержке Минобрнауки РФ.

Литература:

1. Динамический анализ самолета на земле. Рычков С.П. Самарский областной центр новых информационных технологий: 2008 г. – 78 стр.

2. Конструкции и прочность самолетов В.Н. Зайцев, Киев: 1974 – 488 стр.

3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1966. - 992 с.

4. Расчет шасси самолета на прочность: Учеб.пособие/ Л.А. Евсеев, К.В. Миронов, П.А. Фомичев. – Харьков: Харьк.авиац.ин-т, 1988.

5. Бехтина Н Б, Кубланов М С Факторы, определяющие взаимодействие авиационного шасси с взлетно-посадочной полосой U Научный вестник МГТУ ГА Сер Аэромеханика и прочность (М) - 2005 - Ki 81(1,1) -С 80-86