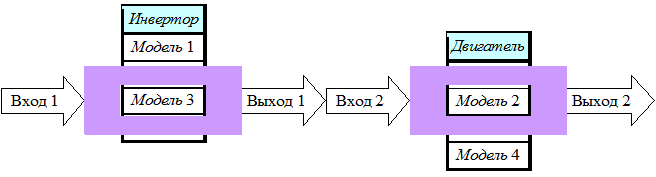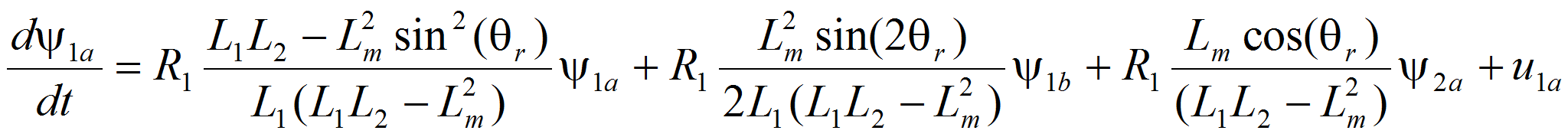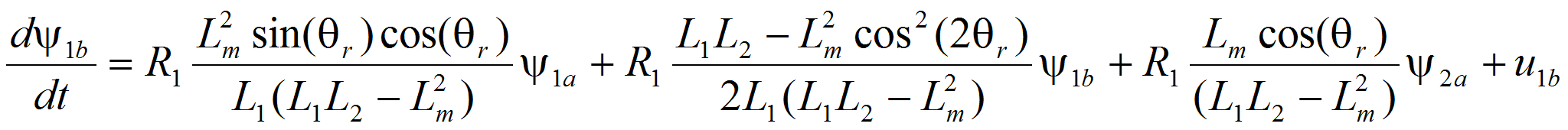Моделирование динамических объектов с использованием систем алгебраических и обыкновенных дифференциальных уравнений является одним из основных этапов автоматизированного проектирования. При этом используются численные методы решения алгебраических и дифференциальных уравнений. Эффективность моделирования можно оценивать по двум показателям — точности и быстроте нахождения решения. Обычно между ними существует противоречие: для повышения точности уменьшают шаг интегрирования, но при этом увеличивается время счёта. Многие исследования в области численных методов посвящены разрешению этого противоречия, но достигнутые результаты пока не позволяют считать проблему решённой.
Одним из возможных путей решения указанной проблемы в соответствии с исследованиями, проводимыми в научно-учебной лаборатории систем автоматизированного проектирования (НУЛ САПР) Института космических и информационных технологий Сибирского федерального университета под руководством профессора С.А. Бронова, является построение системы моделирования с переменной структурой. В данной работе рассматриваются возникающие в этой связи некоторые математические проблемы, пути их решения и полученные на данный момент результаты. Проблема корректного моделирования решается на стыке таких направлений как компьютерное моделирование и информационные системы. Цель данной работы состоит в проверке принципов функционирования системы моделирования с возможностью замены моделей элементов в процессе моделирования на примере простейшей электромеханической системы.
Задачи данной работы заключаются в:
Разработке принципов построения адаптивной модели технического объекта на примере электромеханической системы;
Разработке комплекса математических моделей двигателя двойного питания и инверторов с различной степенью детализации для простейшей электромеханической системы;
Построение нескольких вариантов моделей для синхронного двигателя;
Реализации в существующих математических пакетах программ адаптивной модели электромеханической системы с возможностью замены моделей отдельных элементов.
Моделируемая система представляется моделью в виде совокупности уравнений. Моделирующая система обеспечивает формирование этой общей модели моделируемой системы, выбор и применение методов решения получаемых уравнений. Таким образом, модели и методы их решения составляют две стороны процесса моделирования.
Для улучшения характеристик процесса моделирования в настоящее время в процессе расчётов частично изменяют методы (или их параметры), в частности, могут менять тип метода, шаг интегрирования и т. п.
Предлагается менять также модель в зависимости от того, какой режим рассчитывается в данный момент. Если происходит смена режимов работы в процессе моделирования, то это должно приводить к смене соответствующих моделей (рис.1).
Рис. 1
Возможность смены методов расчёта (или их параметров) также сохраняется, но в данном случае методы (и их параметры) должны подстраиваться к той модели, которая в данный момент является актуальной.
При этом возникает ряд математических проблем обеспечения корректности перехода от одной модели к другой.
Модель системы состоит из частных моделей отдельных модулей. Каждый модуль может иметь несколько вариантов модели: нелинейную и линеаризованную, с большим или малым числом переменных состояния, постоянство (непостоянством, функциональной зависимостью) параметров, вероятностным или детерминированным характером параметров и связей.
Рассматриваемый подход развивается на примере электромеханических систем, в том числе, для систем поворота антенн и солнечных батарей космических аппаратов, прецизионность которых существенно затрудняет их моделирование обычными средствами.
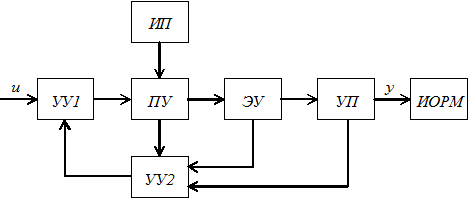
Рис. 2. Структурная схема электромеханической системы
На рис.2 изображена структурная схема электромеханической системы, где обозначены: ИП — источник питания (электрическая сеть, аккумулятор и т.п.); УУ1 и УУ2 — части устройства управления (УУ1 — формирует сигналы управления, УУ2 — собирает информацию об объекте); ПУ — преобразовательное устройство; ЭУ — электродвигательное устройство; УП — передаточное устройство; ИОРМ — исполнительный орган рабочей машины; u — сигнал задания (входной сигнал); y — выходные координаты перемещения ИОРМ
Р
ис.2
Для получения вариантов моделей для одного и того же элемента (например, электродвигателя определённого типа) используются возможности символьного процессора программы MathCAD, формирующего модели при различных условиях и ограничениях в аналитической форме, и программы Simulink, являющейся приложением к пакету MATLAB и реализующей принципы визуального программирования. Для других элементов (редукторов, транзисторных коммутаторов, датчиков, регуляторов) использованы другие подходы к получению вариантов моделей.
Например, модель электромеханической системы в Simulink выглядит следующим образом (рис.3).
Рис.3
В частности, разработаны нелинейные и линеаризованные варианты моделей синхронного двигателя с постоянными магнитами, индукторного двигателя двойного питания, синхронного двигателя, вращающегося трансформатора, фазовращателя при различных допущениях и упрощениях.
Например, вариант модели электрической машины в естественной системе координат:
;
;
;
где
—
потокосцепления;
—
напряжения питания;
—
электромагнитный момент;
,
,
—
сопротивления и индуктивности и взаимная индуктивность обмоток;
—
угол поворота ротора; индексы 1a, 1b
и 2a соответствуют фазным обмоткам (1 —
статора, 2 — ротора).
Вариант модели той же электрической машины в преобразованной системе координат (исчезли тригонометрические функции, что ускоряет расчёты):
;
;
;
,
индексы 1x, 1y и 2x соответствуют фазным обмоткам в преобразованной системе координат.
Смена моделей приводит к необходимости проверки, какие переменные состояния сохранились, какие исчезли, какие появились. Некоторые сценарии смены моделей признаются разрешёнными, другие — запрещёнными. Для разрешённых сценариев предусмотрены алгоритмы пересчёта переменных состояния. В настоящее время работы ведутся с применением программы MathCAD14 как универсального математического инструмента, но предполагается разработка собственного программного продукта для проектирования разнообразных систем.
