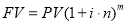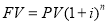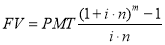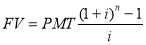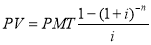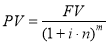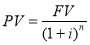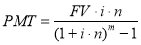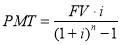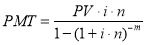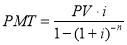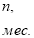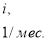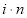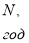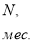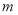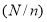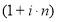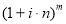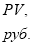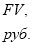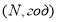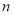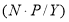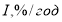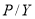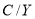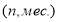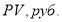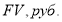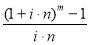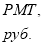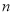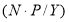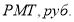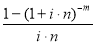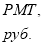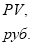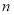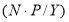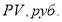Статья посвящена рассмотрению нарушений правил математики в формулах сложных процентов, используемых в доходном подходе при осуществлении оценочной деятельности. Предложены корректировки формул сложных процентов и приведены примеры их использования в стоимостных оценочных расчетах.
Ключевые слова : показатель, размерность, функция, сложный процент, оценочная деятельность .
В оценочной, финансовой, банковской, инвестиционной, страховой и иных видах экономической деятельности широко применяются шесть функций сложного процента, из которых три функции являются базовыми, а три функции — им обратные.
Функциями базовыми являются: 1. Накопленная сумма единицы; 2. Накопление единицы за период;3. Текущая стоимость аннуитета [7, c. 64] .
Обратные функции : 1. Текущая стоимость единицы. 2. Фактор фонда возмещения: 3. Взнос на амортизацию единицы [7, c. 64].
Все шесть функций сложного процента строятся с использованием общей базовой формулы
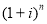
В общей базовой формуле сложного процента показатель
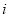
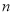
Процентная ставка по своему названию первично измеряется в процентах с последующим переводом в расчетах в десятичные или обыкновенные дроби. Чаще всего в оценочных и финансовых расчетах процентная ставка измеряется в десятичных дробях.
Процентная ставка является периодической, потому что проценты начисляются за определенный временной интервал, который называют периодом начисления. Вкачестве периода начисления процентов принимаются год, полугодие, квартал, месяц или даже день [8, c. 17]. На практике чаще всего употребляются годовые процентные ставки (1/год), которые могут быть переведены в другие единицы измерения.
В учебном пособии по финансовой математике приведены переводы единицы измерения процентной ставки: «
Так, например, если дана годовая процентная ставка
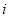

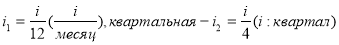
Из приведенных суждений следует, что процентная ставка имеет не только числовое значение, но и временную характеристику (год, квартал, месяц и т. д.).
Как известно, сложный процент применяется в оценочных и финансовых расчетах, связанных с учетом фактора времени, которое чаще в прямой или косвенной форме выражается в общей базовой формуле показателем степени.
В учебнике «Финансовая математика» приведена формула сложного процента
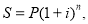
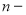
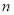
В теори и оценки «время получения инвестиционного дохода измеряется интервалами, или периодами. Интервал, или период, может быть равен дню, неделе, месяцу, кварталу, полугодию или году» [7, c. 35]. Значит, число периодов выражается в единицах времени.
В учебной литературе по оценочной деятельности при иллюстрации доходного подхода приводятся различные примеры применения функций сложного процента, в которых процентная ставка и число периодов в явном виде не имеют единицы измерения (размерности), т. е. принимаются условно в качестве безразмерных величин, что позволяет реализовывать функции сложного процента в экономических расчетах.
Например, в книге «Элементы финансовой математики для оценщиков (курс лекций и сборник задач)» для иллюстрации применения первой функции сложного процента в оценочных расчетах приведена следующая задача:
«Задача 1. Вы хотите положить 100 $ в банк на 3 года. Все банки предлагают одинаковую процентную ставку (10 % годовых), но с разной периодичностью начисления процентов (один раз в год, один раз в полугодие, ежеквартально, ежемесячно). В какой из банков выгоднее вложить деньги?» [9, с. 12] .
Задача для иллюстрации применения первой функции сложного процента имеет вид:
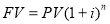
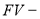
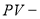
Решение с применением первой функции сложного процента:
— при начислении процентов один раз в год
:
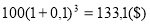
— при начислении процентов один раз в полугодие:
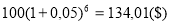
— при начислении процентов ежеквартально:
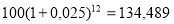
— при начислении процентов ежемесячно:
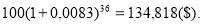
Как видно из приведенной иллюстрации, единицы измерения (размерности) в явном виде у процентной ставки и числа периодов отсутствуют, хотя в преобразованиях, связанных с разной периодичностью начисления процентов, они применяются.
Процентная ставка и число периодов являются экономическими показателями, но без учета в явном виде размерности они теряют свою экономическую природу и становятся просто коэффициентами, что нельзя признать правомерным для учебных примеров и практических расчетов в оценочной деятельности.
В прикладной экономической науке в содержание экономического показателя включают « наименование, числовое значение и единицу измерения » [6, c. 13]. Такое же содержание должны иметь процентная ставка и число периодов в общей базовой формуле и всех функций сложного процента, используемых в оценочной деятельности.
Вопросы учета размерности процентной ставки и числа периодов затрагивались в ряде работ по оценочной деятельности [3, 4, 5]. Однако они ограничивались рассмотрением размерности показателей только первой и четвертой функций сложного процента и не распространялись на остальные его функции.
Если в основании общей базовой формулы сложного процента внести числовое значение и размерность процентной ставки то по правилам математики нельзя суммировать единицу с процентной ставкой, имеющей размерность. Кроме того, по правилам математики нельзя возводить основание общей базовой формулы сложного процента в степень, показатель которой имеет единицу измерения.
Например, при учете размерности процентной ставки и числа периодов формулы, используемые для решения задачи 1, будут иметь следующий вид:
— при начислении процентов один раз в год:
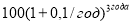
— при начислении процентов один раз в полугодие:
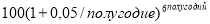
— при начислении процентов ежеквартально:
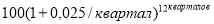
— при начислении процентов ежемесячно:
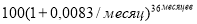
В этих формулах единицы измерения процентной ставки и числа периодов не сокращаются, поэтому такие выражения решения не имеют.
Следовательно, как показатель степени
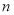
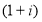
Для решения этой проблемы следует обосновать и внести определенные коррективы в общую базовую формулу и во все функции сложного процента для их реализации в экономических расчетах по правилам математики.
Целью статьи является совершенствование теории и практики оценочной деятельности в рамках доходного подхода путем применения размерности показателей функций сложного процента и обеспечения возможности их реализации в стоимостных оценочных расчетах.
Экономический смысл сложного процента заключается в том, что проценты, начисленные в конце каждого периода, не выплачиваются, а присоединяются к основной сумме вложенного капитала, и в следующий расчетный период процент начисляется уже на большую сумму.
Наряду со сложным процентом в финансовых расчетах применяется и простой процент, в котором базовая формула имеет те же составляющие, но другое выражение —
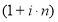
Смысл простого процента заключается в том, что процент начисляется только на первоначальный капитал, а полученная постоянная величина прибыли не участвует в обороте капитала и ее можно использовать после окончания каждого отчетного периода.
В формуле простого процента нет нарушений правил математики, так как при умножении ставки процента в форме десятичной дроби на срок начисления процентов, выраженных в одинаковых единицах времени, происходит сокращение этих единиц измерения. В результате умножения ставки процента на срок начисления процентов получается безразмерная величина, которая может суммироваться с единицей в общей формуле простого процента.
« Переход от простого процента к сложному проценту иллюстрируется на примере инвестора, который по депозитному договору с банком вложил определенную сумму денежных средств на депозитный счет на определенный срок с начислениями по простому проценту. После получения вложенной суммы денег с начисленными процентами инвестор перезаключил договор с банком на следующий такой же срок с начислениями по простому проценту. Число перезаключений депозитного договора инвестора с банком может быть многоразовое, что означает реинвестирование средств, полученных на каждом этапе наращения с помощью постоянной или переменнойставки процента » [5, c. 19].
Схема наращения денежных средств инвестора по простому проценту в результате перезаключений договоров (реинвестирования средств), например для
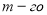
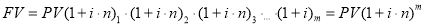
где:
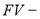
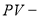
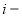
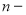
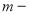
Если в формуле наращения (1) срок начисления процентов у всех перезаключаемых договоров принять равным одному периоду (году, полугодию, кварталу, месяцу и т. д. или определенному числу дней в пределах года), то в этом случае
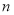
В формуле наращения (1), которая представляет первую функцию сложного процента, как и в общей формуле простого процента, произведение
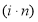
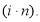
Если периодичность начисления процентов не совпадает с размерностью процентной ставкой, то в этом случае размерность процентной ставки переводится в размерность периодичности начисления процентов. Если заданная периодичность начисления процентов составляет один квартал, тогда и процентная ставка должна выражаться в кварталах.
Например, при числовом значении годовой процентной ставки равной 0,12 в год и заданной периодичности начисления процентов равной одному кварталу, получим скорректированное значение процентной ставки — 0,12/4 квартала = 0,03/ квартал. Тогда произведение будет представлять коэффициент наращения первоначальной суммы вклада за один квартал, который можно суммировать с единицей множителя наращения, как две безразмерные величины (1+0,03=1,03).
Параметр
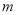

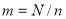
где
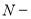
Если общий срок инвестирования средств
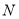
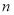
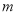
Общая базовая формула сложных процентов после внесения в нее изменений примет следующий вид:
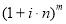
где
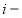
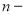
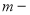
Периодичность начисления процентов
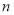
Частота инвестирования капитала
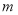
На основе откорректированной общей базовой формулы (3) в таблице 1 представлены откорректированные формулы шести функций сложного процента при платежах в начале периода (Begin).
Таблица 1
Шесть функций сложного процента*
|
Наименование функции |
Формула |
|
|
откорректированная |
действующая [9, с. 7–44] |
|
|
1. Накопленная сумма единицы |
|
|
|
2. Накопление единицы за период |
|
|
|
3. Текущая стоимость аннуитета |
|
|
|
4. Текущая стоимость единицы |
|
|
|
5. Фактор фонда возмещения |
|
|
|
6. Взнос на амортизацию единицы |
|
|
Примечание*. В таблице 1 указаны порядковые номера трех базовых функций и порядковые номера трех обратных им функций, которые используются в их названиях.
Все основные обозначения показателей шести функций сложного процента приняты по аналогии с используемыми в финансовых калькуляторах и оценочной литературе.
Существенное различие между действующими и откорректированными функциями сложного процента заключается в том, что в откорректированных функциях сложного процента процентная ставка сопряжена с периодичностью начисления процентов, что приводит размерность этих показателей к безразмерной величине. Кроме того, показатель
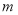
В качестве иллюстрации представим решения задачи 1 при применении первой откорректированной функции сложного процента для случаев начисления процентов:
— при годовом начислении процентов
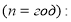
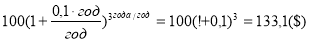
— при полугодовом начислении процентов
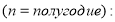
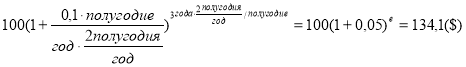
— при квартальном начислении процентов
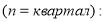
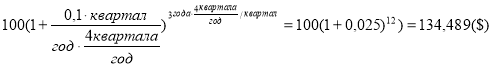
— при ежемесячном начислении процентов (
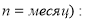
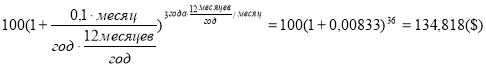
Как видно из решения задачи 1, правила математики в откорректированной первой функции сложного процента соблюдаются, и все расчеты выполнены корректно.
Проведем теперь более общую проверку откорректированных функций сложного процента на числовых примерах и сравним результаты расчета по функциям и по финансовому калькулятору FC-100. Примеры расчета по трем откорректированным функциям наращения (1, 2, 3) сложного процента приведены в табл. 2–4а.
Условные обозначения
:
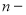
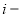
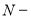
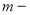
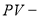
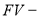
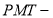
Постоянные исходные данные:
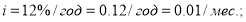
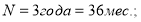
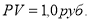
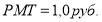
Таблица 2
Исходные данные и
результаты расчета по первой откорректированной функции сложного процента
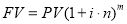
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
0.01 |
0.01 |
3.0 |
36.0 |
36.0 |
1.01 |
1.4307 |
1.0 |
1.430 |
|
2,0 |
0.01 |
0.02 |
3.0 |
36.0 |
18.0 |
1.02 |
1.4283 |
1.0 |
1.428 |
|
3,0 |
0.01 |
0.03 |
3.0 |
36.0 |
12.0 |
1.03 |
1.4257 |
1.0 |
1.425 |
|
4,0 |
0.01 |
0.04 |
3.0 |
36.0 |
9.0 |
1.04 |
1.4233 |
1.0 |
1.423 |
|
5,0 |
0.01 |
0.05 |
3.0 |
36.0 |
7.2 |
1.05 |
1.4208 |
1.0 |
1.420 |
|
6,0 |
0.01 |
0.06 |
3.0 |
36.0 |
6.0 |
1.06 |
1.4185 |
1.0 |
1.418 |
|
7,0 |
0.01 |
0.07 |
3.0 |
36.0 |
5.1 |
1.07 |
1.4159 |
1.0 |
1.415 |
|
8,0 |
0.01 |
0.08 |
3.0 |
36.0 |
4.5 |
1.08 |
1.4138 |
1.0 |
1.413 |
|
9,0 |
0.01 |
0.09 |
3.0 |
36.0 |
4.0 |
1.09 |
1.4115 |
1.0 |
1.411 |
|
10.0 |
0.01 |
0.10 |
3.0 |
36.0 |
3.6 |
1.10 |
1.4093 |
1.0 |
1.409 |
|
11,0 |
0.01 |
0.11 |
3.0 |
36.0 |
3.2 |
1.11 |
1.4067 |
10 |
1.406 |
|
12,0 |
0.01 |
0.12 |
3.0 |
36.0 |
3.0 |
1.12 |
1.4049 |
1.0 |
1.404 |
В таблице 2 изменяется значение периодичности начисления процентов при неизменных значениях процентной ставки и сроков инвестирования. Остальные показатели таблицы 2 являются расчетными в зависимости от изменения периодичности начисления процентов. При увеличении периодичности начисления процентов и одинаковой процентной ставке и сроке инвестирования будущая сумма имеет тенденцию к уменьшению, так как проценты начисляются все реже и реже. Для проверки полученных значений будущей суммы проведем вычисления с использование финансового калькулятора, который имеет некоторые отличительные показатели и их условные обозначения.
Условные обозначения по финансовому калькулятору F С-100:
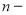
Постоянные исходные данные: n = 3 года = 36 мес.; I =12 % /год = = 0,12/год = 0.01 /мес.: PV= 1.0 руб.
Таблица 2а
Исходные данные и
результаты расчета по первой функции сложного процента по финансовому калькулятору
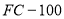
|
|
|
|
|
|
|
|
|
3.0 |
3.0 |
12.0 |
1.0 |
12.0 (1.0) |
1.0 |
1.430 |
|
3.0 |
3.0 |
12.0 |
1.0 |
6.0 (2.0) |
1.0 |
1.428 |
|
3.0 |
3.0 |
12.0 |
1.0 |
4.0 (3.0) |
1.0 |
1.425 |
|
3.0 |
3.0 |
12.0 |
1.0 |
3.0 (4.0) |
1.0 |
1.423 |
|
3.0 |
3.0 |
12.0 |
1.0 |
2.4 (5.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
2.0 (6.0) |
1.0 |
1.418 |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.7 (7.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.5 (8.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.3 (9.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.2 |
1.2 (10.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.1 (11.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.0 (12.0) |
1.0 |
1.404 |
В головке таблицы 2а в скобках указаны условные обозначения показателей, приведенные в таблице 2. Результаты расчета по строкам с целым числом платежей за год полностью совпадают с результатами расчета, по аналогичным строкам, полученными по откорректированным функциям, что свидетельствует о правомерности используемой функции.
Теперь рассмотрим расчеты по второй откорректированной функции сложного процента (табл.3).
Таблица 3
Исходные данные и
результаты расчета по второй откорректированной функции сложного процента
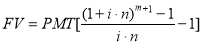
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
0.01 |
0.01 |
3.0 |
36.0 |
36.0 |
1.01 |
43.07 |
1.0 |
43.07 |
|
2,0 |
0.01 |
0.02 |
3.0 |
36.0 |
18.0 |
1.02 |
21.41 |
1.0 |
21.41 |
|
3,0 |
0.01 |
0.03 |
3.0 |
36.0 |
12.0 |
1.03 |
14.19 |
1.0 |
14.19 |
|
4,0 |
0.01 |
0.04 |
3.0 |
36.0 |
9.0 |
1.04 |
10.58 |
1.0 |
10.58 |
|
5,0 |
0.01 |
0.05 |
3.0 |
36.0 |
7.2 |
1.05 |
8.41 |
1.0 |
8.41 |
|
6,0 |
0.01 |
0.06 |
3.0 |
36.0 |
6.0 |
1.06 |
6.97 |
1.0 |
6.97 |
|
7,0 |
0.01 |
0.07 |
3.0 |
36.0 |
5.1 |
1.07 |
5.88 |
1.0 |
5.88 |
|
8,0 |
0.01 |
0.08 |
3.0 |
36.0 |
4.5 |
1.08 |
5.16 |
1.0 |
5.16 |
|
9,0 |
0.01 |
0.09 |
3.0 |
36.0 |
4.0 |
1.09 |
4.57 |
1.0 |
4.57 |
|
10.0 |
0.01 |
0.10 |
3.0 |
36.0 |
3.6 |
1.10 |
4.09 |
1.0 |
4.09 |
|
11,0 |
0.01 |
0.11 |
3.0 |
36.0 |
3.2 |
1.11 |
3.60 |
10 |
3.60 |
|
12,0 |
0.01 |
0.12 |
3.0 |
36.0 |
3.0 |
1.12 |
3.37 |
1.0 |
3.37 |
Сравнительные результаты расчета по второй откорректированной функции с использованием финансового калькулятора приведены в табл. 3а.
Постоянные исходные данные: n = 3 года = 36 мес.; I =12 % /год = = 0,12/год = 0.01 /мес.: PMT= 1.0 руб.
Таблица 3а
Исходные данные и результаты расчета по второй функции сложного процента по финансовому калькулятору FC -100
|
|
|
|
|
|
|
|
|
3.0 |
36.0 |
12.0 |
12.0 |
12.0 (1.0) |
1.0 |
43.07 |
|
3.0 |
18.0 |
12.0 |
6.0 |
6.0 (2.0) |
1.0 |
21.41 |
|
3.0 |
12.0 |
12.0 |
4.0 |
4.0 (3.0) |
1.0 |
14.19 |
|
3.0 |
9.0 |
12.0 |
3.0 |
3.0 (4.0) |
1.0 |
10.58 |
|
3.0 |
7.2 |
12.0 |
2.4 |
2.4 (5.0) |
1.0 |
- |
|
3.0 |
6.0 |
12.0 |
2.0 |
2.0 (6.0) |
1.0 |
6.97 |
|
3.0 |
5.1 |
12.0 |
1.7 |
1.7 (7.0) |
1.0 |
- |
|
3.0 |
4,5 |
12.0 |
1.5 |
1.5 (8.0) |
1.0 |
- |
|
3.0 |
3.9 |
12.0 |
1.3 |
1.3 (9.0) |
1.0 |
- |
|
3.0 |
3.6 |
12.0 |
1.2 |
1.2 (10.0) |
1.0 |
- |
|
3.0 |
3.3 |
12.0 |
1.1 |
1.1 (11.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.0 (12.0) |
1.0 |
3.37 |
В каждой строке таблицы 3а представлено числу платежей за год (P/Y), которому соответствует число начислений процентов за год (C/Y), и число периодов начислений процентов, которое определяется путем умножения числа платежей за год на срок инвестирования, выраженный в годах. Показателя «Срок инвестирования» (N) в данных калькулятора нет, он задается в условиях задачи.
Финансовый калькулятор по не целым значениям показателя P/Y не выдает результаты по FV. По другим показателям C/Y и P/Y данные в таблицах 3 и 3а полностью совпадают. Показатель P/Y определяется, как отношение количества месяцев в году к заданной периодичности начисления процентов, а численное значение показателя P/Y принимается равным значению показателя C/Y. Это означает, что число начислений процентов соответствует числу платежей. Однако число платежей может быть больше, чем число начислений процентов. Например, если число начислений процентов за год составляет 2, а числа платежей в год — 12 при сроке инвестирования 3 года, то FV составит 42.88 руб., что в 6 раз более значения, указанного в таблице 3а (6.97 руб.).
Перейдем к рассмотрению расчетов по третьей функции сложного процента (табл. 4). В литературе по оценке это пятая функция [9, c. 32].
Таблица 4
Исходные данные и
результаты расчета по третьей откорректированной функции сложного процента
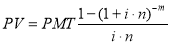
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
0.01 |
0.01 |
3.0 |
36.0 |
36.0 |
1.01 |
30.10 |
1.0 |
30.10 |
|
2,0 |
0.01 |
0.02 |
3.0 |
36.0 |
18.0 |
1.02 |
14.98 |
1.0 |
14.99 |
|
3,0 |
0.01 |
0.03 |
3.0 |
36.0 |
12.0 |
1.03 |
9.95 |
1.0 |
9.95 |
|
4,0 |
0.01 |
0.04 |
3.0 |
36.0 |
9.0 |
1.04 |
7.43 |
1.0 |
7.43 |
|
5,0 |
0.01 |
0.05 |
3.0 |
36.0 |
7.2 |
1.05 |
5.92 |
1.0 |
5.92 |
|
6,0 |
0.01 |
0.06 |
3.0 |
36.0 |
6.0 |
1.06 |
4.91 |
1.0 |
4.91 |
|
7,0 |
0.01 |
0.07 |
3.0 |
36.0 |
5.1 |
1.07 |
4.16 |
1.0 |
4.16 |
|
8,0 |
0.01 |
0.08 |
3.0 |
36.0 |
4.5 |
1.08 |
3.65 |
1.0 |
3.65 |
|
9,0 |
0.01 |
0.09 |
3.0 |
36.0 |
4.0 |
1.09 |
3.23 |
1.0 |
3.23 |
|
10.0 |
0.01 |
0.10 |
3.0 |
36.0 |
3.6 |
1.10 |
2.64 |
1.0 |
2.64 |
|
11,0 |
0.01 |
0.11 |
3.0 |
36.0 |
3.2 |
1.11 |
2.58 |
10 |
2.58 |
|
12,0 |
0.01 |
0.12 |
3.0 |
36.0 |
3.0 |
1.12 |
2.40 |
1.0 |
2.40 |
Сравнительные результаты расчета по третьей функции сложного процента с использованием финансового калькулятора приведены в табл.4а.
Постоянные исходные данные: n = 3 года = 36 мес.; I =12 % /год = = 0,12/год = 0.01 /мес.; PMT= 1.0 руб.
Таблица 4а
Исходные данные и результаты расчета по третьей функции сложного процента по финансовому калькулятору FC -100
|
|
|
|
|
|
|
|
|
3.0 |
36.0 |
12.0 |
12.0 |
12.0 (1.0) |
1.0 |
30.10 |
|
3.0 |
18.0 |
12.0 |
6.0 |
6.0 (2.0) |
1.0 |
14.99 |
|
3.0 |
12.0 |
12.0 |
4.0 |
4.0 (3.0) |
1.0 |
9.95 |
|
3.0 |
9.0 |
12.0 |
3.0 |
3.0 (4.0) |
1.0 |
7.43 |
|
3.0 |
7.2 |
12.0 |
2.4 |
2.4 (5.0) |
1.0 |
- |
|
3.0 |
6.0 |
12.0 |
2.0 |
2.0 (6.0) |
1.0 |
4.91 |
|
3.0 |
5.1 |
12.0 |
1.7 |
1.7 (7.0) |
1.0 |
- |
|
3.0 |
4,5 |
12.0 |
1.5 |
1.5 (8.0) |
1.0 |
- |
|
3.0 |
3.9 |
12.0 |
1.3 |
1.3 (9.0) |
1.0 |
- |
|
3.0 |
3.6 |
12.0 |
1.2 |
1.2 (10.0) |
1.0 |
- |
|
3.0 |
3.3 |
12.0 |
1.1 |
1.1 (11.0) |
1.0 |
- |
|
3.0 |
3.0 |
12.0 |
1.0 |
1.0 (12.0) |
1.0 |
2.40 |
В таблице 4а результаты расчета PV по целым числам C/Y и P/Y полностью совпадают с аналогичными результатами, приведенными в таблице 4. По дробным числам C/Y и P/Y финансовый калькулятор выдает ошибку, т. е. не выдает числовое значение, что с точки зрения здравого смысла является правильным, так как число платежей (P/Y) не может быть дробным числом.
По трем остальным функциям сложного процента расчеты не приводятся, так как они являются обратными основным функциям наращения и не изменяют технику вычислений.
ВЫВОДЫ:
В учебной литературе по оценочной деятельности в общей базовой формуле сложного процента ставка процента и число периодов используются без указания единиц измерения, что является неправомерным.
При установлении единицы измерения процентной ставки и числа периодов по правилам математики в основании общей базовой формулы сложного процента нельзя суммировать единицу с процентной ставкой, имеющей размерность. Также нельзя по правилам математики возводить основание общей базовой формулы сложного процента
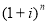
Для корректировки общей базовой формулы и всех функций сложного процента предложено внести дополнительные показатели, характеризующие периодичность начисления процентов, срок и частоту инвестирования капитала, что позволяет реализовывать функции сложного процента без нарушения правил математики.
Приведены примеры использования откорректированных формул сложных процентов в стоимостных оценочных расчетах.
Статья может быть полезна слушателям системы повышения квалификации оценщиков, практикующим оценщикам, предпринимателям, инвесторам, финансистам, страховщикам и иным лицам.
Литература:
- Бадюков В. Ф. Финансовая математика: учеб. пособие / В. Ф. Бадюков,
- М. Ю. Серкин. Хабаровск: РИЦ ХГАЭП, 2009. 92 с.
- Грибовский С. В. Методы капитализации доходов. Курс лекций. Санкт-Петербург, 1977. 172 с.
- Мочулаев В. Е. К вопросу о безразмерных показателях в теории оценки стоимости недвижимости // Молодой ученый, 2014. № 18. С. 415–420.
- Мочулаев В. Е. Уточненная формула сложных процентов и ее применение в теории оценки стоимости недвижимости // Конкурентоспособность в глобальном мире: экономика, наука, технологии. 2016. № 7. ч.1. С. 242–245.
- Мочулаев В. Е. Методы накопления и дисконтирования денежных потоков в теории оценки стоимости предприятия (бизнеса) // Вопросы оценки, 2016. № 4. С.16–22.
- Курс экономики: Учебник / Под ред. Б. А. Райзберга. М.: ИНФРА-М, 1997. 720 с.
- Фридман Дж., Ордуэй Ник. Анализ и оценка приносящей доход недвижимости. Пер. с англ., М.: «Дело Лтд», 1995. 480 с.
- Четыркин Е. М. Финансовая математика: Учебник. 4- е изд. М: Дело, 2004. 400 с.
- Элементы финансовой математики для оценщиков (курс лекций и сборник задач). Составитель и ответственный редактор канд. физ.- мат. наук, зам. директора ПИНО Т. Г. Касьяненко. СПб., ЗАО «ПИНО», 1997. 64 с.