В статье авторы рассматривают симметрии в теоретической физике, показывают их роль и применение, а также их следствия при преобразованиях.
Ключевые слова: симметрия, преобразования, инвариантность, трансляции, вращения, калибровочные преобразования.
Слово «симметрия» («συμμετρία») имеет греческое происхождение и означает «соразмерность». В повседневном языке под симметрией чаще всего понимают упорядоченность, гармонию и соразмерность. В широком смысле — неизменность (инвариантность), проявляемые при каких-либо преобразованиях или изменениях. Так, например, двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Научное определение симметрии было предложено немецким математиком Германом Вейльем (1885–1955). Согласно ему, под симметрией следует понимать неизменность (инвариантность) какого-либо объекта при определенного рода преобразованиях. При этом не только материальные объекты могут подчиняться законам симметрии, но и математические объекты. Что позволяет применять симметрию к различным законам физики. К примеру, можно говорить об инвариантности тех или иных функций и уравнений при преобразованиях систем координат. Математически общие симметрийные свойства описываются с помощью теории групп.
По мере своего развития физика открывает всё новые виды симметрии законов природы: так если вначале рассматривались пространственно-временные преобразования, то в дальнейшем были установлены не геометрические виды симметрии такие как: калибровочная, перестановочная, унитарная и др.
Роль принципов инвариантности в современной теоретической физике очень большая: с их помощью были предсказаны новые законы сохранения, облегчено решение многих фундаментальных и прикладных задач, выведены сохраняющиеся величины и, что особенно важно, удалось добиться первых успехов на пути объединения фундаментальных взаимодействий.
Существует несколько основных видов преобразований в физике: трансляция времени, трансляции пространства, группы Лоренца или же бусты, вращения пространства и калибровочные преобразования.
Одним из наиболее наглядных видов симметрии является пространственная симметрия, которая имеет большой ряд разновидностей: трансляционная, вращательная, зеркальная и др. К примеру, сфера обладает вращательной симметрией, т. е. при повороте сферы вокруг оси проходящей через центр её центр на любой угол φ не меняет положение сферы (рис. 1). Вращательные операции симметрии сферы образуют группу вращений R .
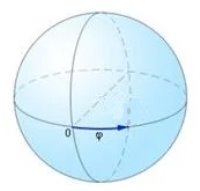
Рис. 1. Поворот сферы на угол φ
Однако стоит заметить, что вместо преобразования самого объекта можно производить соответствующие преобразования системы координат. Если после преобразования координат объект занимает тоже положение что и в старой системе координат, то такое преобразование координат есть преобразование симметрии объекта. Такое определение симметрии намного удобнее, когда мы имеем дело с уравнениями, функциями или операторами. Если математический объект остается инвариантным при определенном преобразовании координат, то это преобразование считается операцией симметрии этого объекта. Совокупность операций симметрии любого объекта образует группу симметрии этого объекта.
Из выше сказанного, можно говорить о симметрии физических законов, поскольку они выражаются математическими выражениями. Например, закон всемирного тяготения гласит, что сила взаимного притяжения между двумя телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между телами. Из чего следует, что сила не зависит от положения пары тел, но зависит от расстояния между ними. Это означает, что данный закон инвариантен относительно трансляции(переноса) или вращений системы координат. Это не было бы так, если бы пространство не было однородным и изотропным. Такая переносная (трансляционная) симметрия является еще одной разновидностью пространственной симметрии. Закон движения F = mā, не изменяет свой вид при переносе начала координат в другую точку. То же самое происходит при поворотах системы координат. Этот закон движения, так же как и закон всемирного тяготения инвариантен относительно сдвигов и поворотов системы координат. Каждому типу непрерывной симметрии сопоставляется сохраняющаяся величина. Так инвариантность относительно сдвигов в пространстве приводит к закону сохранения импульса, а инвариантность относительно вращений, а закону сохранения момента импульса.
Другой разновидностью симметрии выступает инвариантность физических законов относительно сдвигов (трансляций) во времени. Например, можно представить эксперимент, который проводят в замкнутой системе, удаленной от любых источников возмущения. Эксперимент проходит при определённых начальных условиях, продолжается заданный период времени и в итоге завершается определённым результатом. Затем его через некоторый промежуток времени повторяют в таких же условиях и получают тот же результат. В таком случае говорят, что система симметрична относительно сдвига во времени.
Инвариантность относительно трансляции во времени не всегда имеет место. К примеру, влияние расширения Вселенной на лабораторные эксперименты обычно пренебрежительно мало, но принципиально существует. При достаточной точности эксперимент, начатый позже, даст иной результат, чем такой же эксперимент, начатый раньше. Инвариантность системы относительно сдвигов во времени приводит к закону сохранения энергии.
Калибровочные преобразования — это преобразования потенциалов, при которых не меняются математические выражения. К примеру, можно рассмотреть простую электрическую цепь(рис.2), состоящую из источника питания напряжением 3 вольт и резисторов с сопротивлениями 1 и 2 Ом.
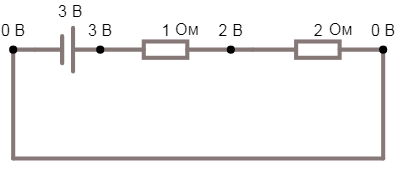
Рис. 2. Электрическая цепь, в которой черными точками обозначены узлы
Через цепь протекает электрический ток в 1 ампер. На каждом элементе цепи можно вольтметром померить напряжение. Напряжение по определению являться разностью потенциалов, можно в каком-нибудь узле задать нулевой потенциал и посчитать потенциалы остальных узлов схемы, обычно за ноль берут минус источника питания (рис. 2). Напряжение между двумя любыми узлами — это разность соответствующих потенциалов. Так на первом резисторе сопротивлением 1 Ом, напряжение будет 1 вольт. Стоит заметить, что если ко всем потенциалам электрической схемы добавить число, допустим 15 вольт, то это не скажется на напряжениях (рис 3)
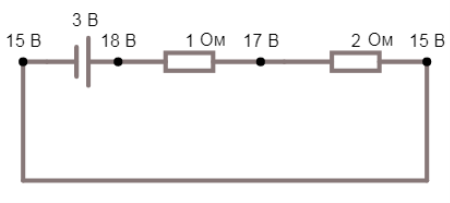
Рис. 3. Электрическая цепь с увеличенными потенциалами в узлах на 15 вольт
В данном случае мы наблюдаем симметрию относительно калибровочных преобразований. Калибровочная инвариантность в соответствии с теоремой Нётер влечёт за собой закон сохранения электрического заряда в квантовой электродинамике.
В теоретической физике инвариантность приводит к появлению различных сохраняющихся величин, законов сохранения, упрощению различных математических операций, уравнений и операторов.
Литература:
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособие. — 10-ти т. I. Механика, — 4-е изд., испр. — М.: Наука. 1988 Гл. ред. физ.-мат. лит., 1988. — 216 с.
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика. М., 1989.
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — М., 2016.
- Любарский Г. Я. Теория групп и физика. М., 1986
- Ферми Э. Квантовая механика. — М.: Мир, 1968. — 366 с.







