Тема «дифференциальные уравнения» — один из крупнейших разделов современной математики. Он пересекается со многими сферами деятельности. Дифференциальные уравнения широко используются на практике. Тема данной работы всегда остается актуальной, так как математические методы используются при решении многих задач, в том числе и в области медицины. Каждый год ученые выявляют все новые заболевания, находят лекарства, новые методы лечения. Все это было бы невозможно без математики. При изучении любого явления сначала создается его математическая модель, которая описывает основные закономерности, которым математически подчинено это явление. В наших примерах эти законы выражались в виде дифференциальных уравнений. Математические модели облегчают прогнозирование результатов эксперимента, проведенного в реальных системах, позволяют исследовать явление в целом, прогнозировать его развитие, изменения, происходящие с течением времени. В предлагаемой работе мы рассмотрели применение дифференциальных уравнений для решения задач в медицине на примере модели растворения лекарственных форм лекарственных препаратов в таблетках, моделирования лечения онкологических заболеваний.
Ключевые слова: дифференциальные уравнения, медицина, применение дифференциальных уравнений, уравнение.
Қазіргі әлемде болып жатқан процестер мамандардан сапалы және терең білімді қажет етеді. Бүгінде жаһанданудың арқасында жыл сайын техника жақсарып, медицина саласында жаңа білім мен зерттеулер пайда болуда.
Техниканы құру үшін адамдар дифференциалдық теңдеулерсіз жасай алмайтын есептеулерді қажет етеді. Қазіргі әлемде медициналық персоналдың математикалық модельдеуді, статистиканы және практикада қолданылатын басқа құбылыстарды қолданумен байланысты қызметі өзгеруде [1].
Медицинадағы математиканың рөлі диагностикалық процедураларды жүргізуге ықпал етеді. Қазіргі уақытта ауруларды емдеу және диагностикалау әдістері айтарлықтай кеңейді. Медициналық орталықтардың едәуір бөлігі математикалық модельдеу әдістерін қолданады. Бұл диагноздардың басым көпшілігінің дәлдігін арттырады. Математиканың негіздері туралы білімді дәрігерлер адам ағзасындағы процестерді сипаттау үшін қолданады. Көптеген оқу орындарында студенттер негізгі медициналық пәндермен қатар математиканы да оқиды. Қолданбалы математиканың негізгі мәселесі-бастапқы математикалық модельді таңдау, және бұл биология мен медицинадағыдай білімнің ешқандай саласында cезілмейді [1].
Медицинада дифференциалдық теңдеулерді қолданатын бірнеше мысал келтірейік:
— қан ағымының жылдамдығын, клапандар мен жүрек қабырғаларының қозғалыс жылдамдығын анықтау (эхокардиография), қанның тұтқырлығын және гемодинамиканың басқа параметрлерін анықтау үшін;
— ультрадыбыстың биомедициналық қосымшаларын сипаттау үшін: эхоэнцефалограмма, УДЗ, ультрадыбыстық физиотерапия, ультрадыбыстық локация және кардиография;
— адам мен жануарлардың дыбыс қабылдайтын және дыбыс шығаратын мүшелерінің құрылысы мен жұмысын зерттейтін физиологиялық акустика процестерін сипаттау үшін;
— уақытқа байланысты микроорганизмдер популяциясы санының өзгеру функциясын анықтау үшін қолданылады [2].
- Таблетк адан заттың дәрілік формаларының еру з аңы
Таблеткадан заттың дәрілік формаларының еру жылдамдығы таблеткадағы заттың дәрілік формаларының мөлшеріне пропорционалды.
Демек таблеткадағы заттың дәрілік формасының мөлшерінің өзгеруін уақытқа тәуелді етіп енгізу қажет.
Таблеткадағы заттың мөлшерін m деп, ал еру уақытын t деп белгілейміз. Сонда

түріндегі теңдеуді аламыз. Мұндағы k – тұрақты еру жылдамдығы. Минус белгісі уақыт аралығында заттың дәрілік формаларының мөлшері азаятынын білдіреді. (1) теңдеуі шешетін болсақ:
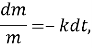
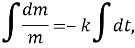
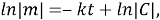
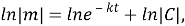

деген нәтижені аламыз. Егер де
t=0, m=
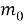
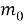

Мұндағы
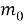
Мысалды қарастайық:
Дәрілік препараттың қандағы концентрациясы организмнен шығарылған заттың әсерінен төмендейді. Концентрацияның төмендеу жылдамдығы қазіргі уақытта заттың концентрациясына пропорционалды. Егер бастапқы уақытта ол 0,4 мг/л-ге тең болса және 20 сағаттан кейін ол екі есе азайса, қандағы осы зат концентрациясының уақытқа тәуелділігін анықтаңыз.
Шешуі: Бұл процесті сипаттайтын теңдеу:
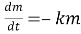
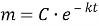
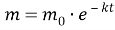
Есептің шарты бойынша
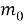
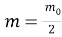
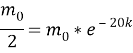
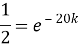
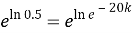
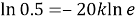
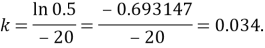
Жауабы: Қандағы зат концентрациясының уақытқа тәуелділігі келесідей өрнектеледі:
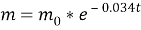
- «Жыртқыш-жемтік» моделі
«Жыртқыш-жемтік» моделі қазіргі уақытта медицинада қолданылады. Қатерлі ісік ауруын модельдеу кезінде ісік жасушалары құрбан болып саналады, ал лимфоциттер оларды жыртқыш ретінде басады. Бұл әдістер дәрігерлерге оңтайлы емдеу жолын анықтауға және олармен күресудің жаңа құралдарын жасауға көмектеседі.
x — ісік жасушаларының саны,
y — лимфоцит жасушаларының саны болсын.
Уақыт өте келе ісік жасушалары мен лимфоциттердің саны уақыт өте келе өзгеретін болғандықтан, онда t уақытына тәуелді x және y үздіксіз функциялар деп санаймыз.
x және у — модельдің күйі деп атаймыз. Модельдің күйі қалай өзгеретінін табыңыз.
Қарастырайық:
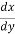
Егер ісік жасушалары болмаса, лимфоциттер саны азаяды. Бұл тәуелділік сызықтық болып саналады:
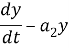
Экожүйеде әр түрдің санының өзгеру жылдамдығы оның санына пропорционалды деп саналады, бірақ тек басқа түрдің жеке тұлғаларының санына байланысты коэффициентпен. Ісік жасушалары үшін бұл коэффициент лимфоциттер санының көбеюімен азаяды, ал лимфоциттер үшін ісік жасушаларының көбеюімен артады. Бұл тәуелділік сызықтық болады. Сондықтан дифференциалдық теңдеулер жүйесін аламыз:
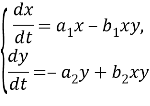
Алынған теңдеулер жүйесі Лотки-Вольтерра моделі деп аталады.
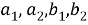
Модель күйінің өзгеру сипаты (x, y) параметрлердің мәндерімен анықталады. Осы теңдеулер жүйесін шеше отырып, денсаулық жағдайының өзгеру заңдылықтарын зерттеуге болады [4].
Кез-келген құбылысты зерттеу кезінде алдымен оның математикалық моделі жасалады, ол осы құбылыс математикалық түрде бағынатын негізгі заңдылықтарды сипаттайды. Біздің мысалдарымызда бұл заңдар дифференциалдық теңдеулер түрінде айтылды. Математикалық модельдер нақты жүйелерде жүргізілген эксперимент нәтижелерін болжауды жеңілдетеді, құбылысты тұтастай зерттеуге, оның дамуын, уақыт өте келе болатын өзгерістерді болжауға мүмкіндік береді. Ұсынылған жұмыста біз дәрі-дәрмектердің дәрілік формаларын таблеткадан еріту моделі, онкологиялық ауруларды емдеуді модельдеу мысалында медицинадағы мәселелерді шешу үшін дифференциалдық теңдеулерді қолдануды қарастырдық.
Дифференциалдық теңдеулерді шешудің математикалық аппараты іс жүзінде жаратылыстану циклінің көптеген мәселелерін шешуге мүмкіндік береді.
Дифференциалдық теңдеулер тек медицина саласында емес, жалпы жаратылыстану ғылымдарының арасында кең көлемде қолданысқа ие. Г.Галелей табиғаттың кез келген құбылысы математикаға тәуелді деген екен. Міне, жай ғана математиканың дифференциалдық теңдеулер саласы медицинаның көптеген саласында қолданылатынын көрсеттім. Түрлі процесстер мен құбылыстардың математикалық модельдері дифференциалдық теңдеулер есептеріне келтірілетіндіктен, бұларды зерттеу мен шешу әдістерін үйренудің қажеттілігі айқын.
Әдебиет:
- Баврин И. И. Высшая математика Учебное пособие для студентов хим.- биол. фак. пед. ин-тов М., Просвещение, 2006, 240 с.
- Гилярова, М. Г. Математика для медицинских колледжей / М. Г. Гилярова. –Ростов н/Д: Феникс, 2011. — 416с.
- Закон растворения лекарственных форм вещества из таблеток [Электронный ресурс] // Poznayka.org. — Режим доступа: https://poznayka.org/s8157t1.html. — Дата доступа: 19.03.2019.
- Рубецков, Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней / Д. И. Рубецков // Известия Вузов. Прикладная нелинейная динамика. — 2011. — № 2. — С. 69–87.426







