Статья посвящена описанию процесса проектирования и разработки сумматора для сложения в байтовом формате.
Ключевые слова: логический элемент, байтовый формат, полусумматор, сумматор, electronics workbench.
Введение
Одним из основных арифметических узлов ЭВМ является сумматор. Это так, потому что большинство математических операций (вычитание, умножение, деление, вычисление тригонометрических функций, извлечение корня и т. д.) можно свести к единственной операции сложения прямых, обратных или сдвинутых на определенное число разрядов кодов чисел.
Полусумматоры
Полусумматор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и P, где S — это бит суммы по модулю, а P — бит переноса. Схема полусумматора изображена на рисунке 1.
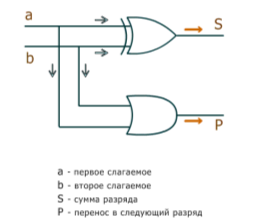
Рис. 1. Схема полусумматора
Простейшим вариантом сложения является сложение двух одноразрядных двоичных чисел, при котором возможны варианты:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10.
Операция суммирования двух одноразрядных чисел совпадает с логической функцией Исключающее ИЛИ, которая характеризуется таблицей истинности, представленной на рисунке 2. Логическим уравнением, полученным из этой таблицы, является
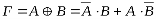
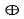
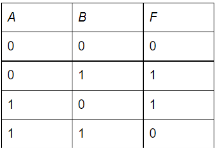
Рис. 2. Суммирования двух одноразрядных чисел
Полные сумматоры
Сумматор — это узел ЭВМ, в котором суммируются коды чисел. Сумматоры многоразрядных чисел, которыми оперирует машина, составляются из одноразрядных сумматоров. Как правило, любой сумматор представляет собой комбинацию одноразрядных сумматоров. Сумматоры различают по принципам построения: накапливающего типа и комбинационного типа.
Сумматоры накапливающего типа строят на сложных JKRS-триггерах, дополняя их выходы достаточно сложными схемами формирования и распространения переносов. Процесс сложения при этом осуществляется поэтапно. Сначала на триггерах сумматора фиксируется код первого операнда, затем на счетные коды разрядов подается код второго операнда. По зависимостям на каждом триггере формируются одноразрядные суммы и значения переносов между разрядами. Учет возникающих переносов задерживает формирование окончательного результата суммы и может требовать дополнительных тактов сложения. Из-за этого многоразрядные схемы сумматора накапливающего типа используются достаточно редко.
Более часто для построения сумматоров используются сумматоры комбинационного типа. Обычно у такого сумматора на входе и выходе имеются регистры для хранения и преобразования кодов операндов и результата.
В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа. Чтобы учесть перенос получается схема из двух полусумматоров. Схема сумматора на рисунке 3.
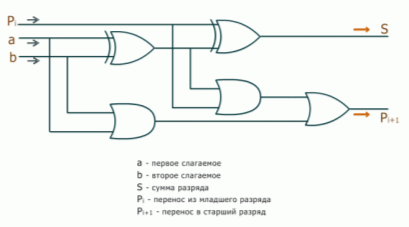
Рис. 3. Схема сумматора
Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определим сумму текущего разряда. С помощью ИСКЛЮЧАЮЩЕГО ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее, ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0.
Теперь рассмотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль входят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т. е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности, представленной на рисунке 4.
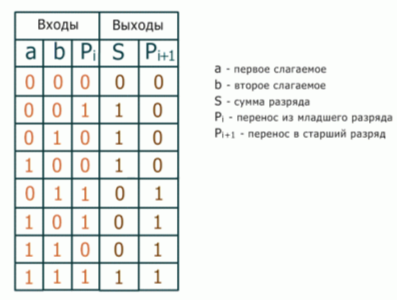
Рис. 4. Таблица истинности сумматора
Разработка схемы байтового сумматора
Необходимо собрать схему многоразрядного сумматора. Многоразрядный сумматор создается на базе одного полусумматора и полных сумматоров. В одном байте восемь бит, следовательно нам понадобится один полусумматор и семь полных сумматоров.
Числа для сложения будут заданы в генераторе слов. Первые 8 бит — первое число, вторые восемь бит — второе число.
Результат сложения покажут индикаторы. При условии, что сумматор был бы меньше чем на восемь бит, мы могли бы использовать индикатор дисплей на 4 или на 7 входов. Но так как 7 входов для байтового сумматора мало, используем индикатор красный зонд для каждой суммы. Получится ряд из восьми индикаторов, который покажет двоичную запись числа результата.
Схема байтового сумматора на рисунке 5. Числа в генераторе слов записываются справа налево. Восемь правых бит — это число B. Каждый бит начиная с самого правого подключается к блокам полусумматора и сумматоров начиная с полусумматора. Восемь левых бит — это число A. Подключение происходит аналогично числу B, но на вход A.
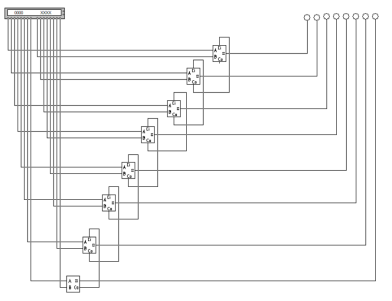
Рис. 5. Схема байтового сумматора
Результаты работы программы
Чтобы проверить работу программы, запустим ее несколько раз с различными входными данными.
1) 3 + 5 = 8, в двоичном представлении 1000. Результат на рисунке 6.
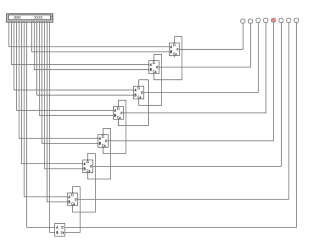
Рис. 6. 3 + 5 = 8, в двоичном представлении 1000
2) 7 + 6 = 13, в двоичном представлении 1101. Результат на рисунке 7.
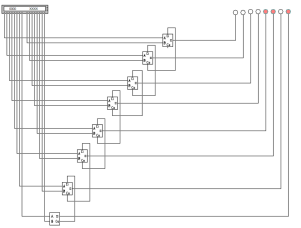
Рис. 7. 7 + 6 = 13, в двоичном представлении 1101
3) 125 + 130 = 255, в двоичном представлении 11111111. Результат на рисунке 8.
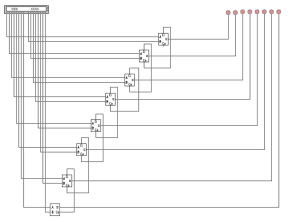
Рис. 8. 125 + 130 = 255, в двоичном представлении 11111111
Расчет мощности и надежности
Значения потребляемой мощности на основе справочных данных для каждого элемента определяем по формуле
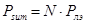
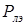
В схеме байтового сумматора 8 элементов. Один полусумматор и 7 сумматоров. Потребляемая мощность элементов указана в таблице 1.
Таблица 1
Потребляемая мощность элементов
|
Элемент |
Мощность, Вт |
Количество элементов |
|
Полусумматор |
1,05 |
1 |
|
Сумматор |
1,05 |
7 |
Следовательно мощность разрабатываемого устройства будет равна 1*1,05 + 7*1,05, то есть 8,4 Вт.
Среднее время наработки до отказа считаем по формуле:
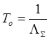
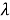
Таблица 2
Потребляемая мощность элементов
|
Элемент |
Интенсивность отказа
|
Количество элементов |
|
Полусумматор |
0,023 |
1 |
|
Сумматор |
0,023 |
7 |
Следовательно среднее время наработки до отказа будет равно 1/(0,023*1*10– 6 + 0,023*7*10– 6 ), то есть 184000 часов. Из данных расчетов можно сделать вывод о высокой надежности.
Заключение
В результате работы спроектирован и разработан сумматора для сложения в байтовом формате. Мощность устройства равна 8,4 Вт, среднее время наработки 184000 часов.
Литература:
- М. А. Карцев. Арифметика цифровых машин. Главная редакция физико-математической литературы издательства «Наука», 1969, 576 с.
- Лю, Цо-Кай; Хохулин, Кейт Р.; Шиау, Лих-Эр; Мурога, Сабуро (январь 1974 г.). «Оптимальные однобитовые полные сумматоры с разными типами вентилей», 1995, 243 с.
- Сведения о полусумматоре [Электронный ресурс]. — https://ru.wikipedia.org/wiki/Полусумматор
- Сведения о сумматоре [Электронный ресурс]. — https://inf1.info/adder