Существует три подхода к определению понятия суммы ряда чисел [1]: в первом случае понятие суммы бесконечного числа членов считается бессмысленным. Сторонники второго подхода считали, что любая сумма может быть бесконечным множеством и что сумма может быть определена с помощью арифметических операций. При третьем подходе выделяются только те, которые могут быть включены в понятие суммы во всех числовых рядах, а остальные не исследуются. Этот подход, основанный на теории пределов, оказался очень эффективным. Этот подход все еще развивается сегодня в результате расширения класса множеств.
Рассмотрим задачу суммирования расходящихся рядов путем сведения к повторному ряду. Если сумма ряда определяется иначе, чем традиционным методом, ее принято называть обобщенной суммой ряда [2].
Как видите, ниже приводится краткое изложение.
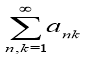
называется двойным рядом.
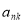
В приложении математического анализа (1) двойной ряд часто рассматривается как повторяющийся ряд по внешнему виду:
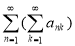
или
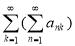

В частности, можно заметить, что следующие повторяющиеся ряды со специальным видом эффективны при суммирования расходящихся рядов:
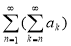
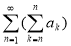
Расходящиеся знакопеременные ряды можно классифицировать по таким трем классом [2]:
1.
Ряды с постоянным радиусом обвертывания:
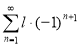
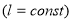
Сумма такого ряда равна
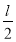
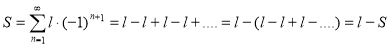
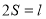
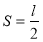
2.
Ряды с ограниченным радиусом обвертывания:
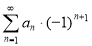
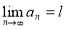
3. Ряды с бесконечным радиусом обвертывания:
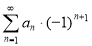
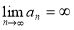
Ниже мы рассмотрим формулы суммирования расходящихся рядов с использованием специальных повторяющихся рядов, которые нужны на практике:
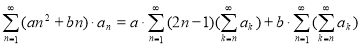
Доказательство:
Справа налево уравнения:
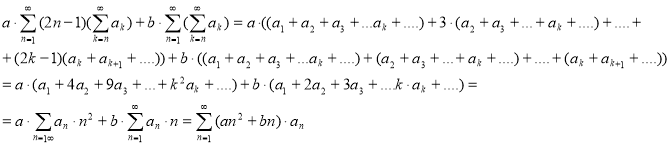
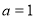
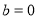
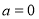
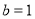
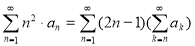
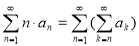
Задача 1. Рассчитайте сумму ниже:
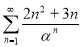
Решение:
Согласно формуле (1):
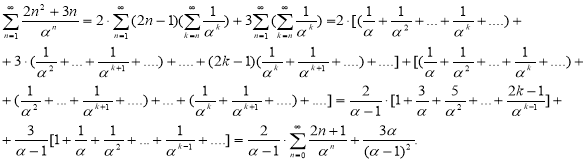
Еще раз используем (1):
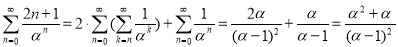
Как результат,
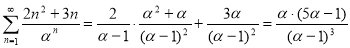
Приведем теперь примеры суммирования расходящихся рядов по следующим формулам, доказанным в [2]:
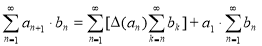
где
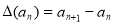
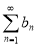
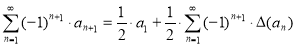

Доказательство этого утверждения дается предположением
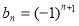
Задача 2. Найдите сумму следующего ряда:
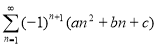
Решение :
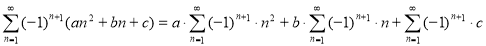
Согласно формуле (3):
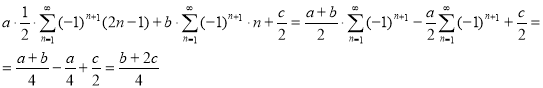
В этом случае результат не зависит от
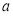
Задача 3. Найдите сумму следующего ряда:
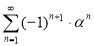
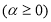
Решение:
Согласно формуле (3):
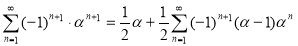
Запишем правую и левую части уравнения следующим образом:
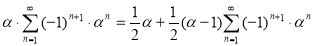
Подводить итоги,
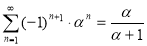
Задача 4. Найдите сумму следующего ряда:
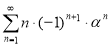
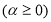
Решение:
Согласно формуле (3):
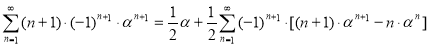
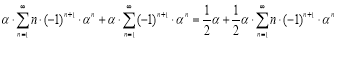
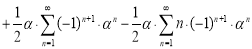
Упрощая это выражение, приходим к равенству
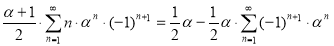
На основе суммы, найденной в задаче 3 выше (
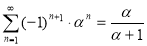
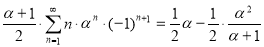
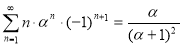
Литература:
- Alimov Sh.O. Ashurov R. R. Matematik tahlil. (1-qism). Toshkent. “Kamolot-press”, 2012. 616-b.
- Пономаренко А. Н. Метод суммирования расходящихся рядов путем сведения к повторному ряду//Молодой учёный.№ 12. 2013.
- Фихтенгольц Г. М. Курс дифференциального и интегральногo исчисления. — М: Наука, 1966.







