Основными причинами здесь, безусловно, являются трудности, определяемые спецификой самой деятельности по решению этих задач: ее неалгоритмичность, необходимость комплексного использования знаний и умений, переноса их в новые условия. Важную роль играет также недостаточная разработанность методики введения теоретических вопросов, связанных с этими задачами, и, как следствие, обращение педагогов к чувственной основе действий, что выражается, например, в предложениях: «представьте, что параметр — это конкретное число, но не забывайте, что это переменная», «иногда удобно рассматривать уравнение с параметром как функцию», «для решения задачи необходимо выбрать управление значения параметра таким образом, что на полученных интервалах решение уравнения (неравенства) подчиняется алгоритму, но найти их сразу невозможно» и т. п.
Другой причиной является низкая эффективность методики обучения, основанной на группировке упражнений по видам выражений (линейные, квадратичные, целые, рациональные, дробно-рациональные, иррациональные, тригонометрические, логарифмические, экспоненциальные), так как в этом случае неправильно определяется стратегия решения для типа выражения. Например, меняя только положение параметра в структуре линейного уравнения, мы приходим к трем различным стратегиям его решения («последовательное преобразование», «интервальное исследование», «факторизация»).
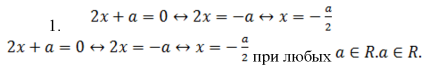
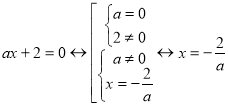
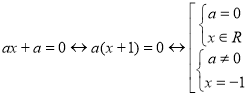
Предлагаемая методика предполагает другой способ планирования содержания обучения, а именно по видам требований задач с параметром, так как различие между переменными (неизвестным и параметром), а следовательно и специфика задач проявляются лишь относительно заданной цели деятельности. Это дает следующую последовательность изучения уравнений и неравенств с параметром.
Таблица 1
|
Тема |
Основное содержание |
|
Уравнения и неравенства с параметром: основные понятия |
Уравнение (неравенство) с двумя переменными, связь переменных, неизвестная и параметр, уравнение (неравенство) с параметром, область допустимых значений, область допустимых значений параметра, область возможных значений неизвестной, решение (а ; х), корень х(а), виды задач. |
|
Задачи на нахождение множества корней уравнения (неравенства) зависимости от параметра |
Критерии успешности решения, формула зависимости x(a) , контрольные значения параметра, условия выделения контрольных значений параметра, их связь с видом выражений |
|
Задачи на нахождение значений параметра, удовлетворяющих условиям, на множество корней |
Критерии успешности решения, виды условий, накладываемых на корни уравнения (неравенства), их роль в определении стратегии решения; приемы решения, их связь с видом выражений |
|
Задачи, сводящиеся к решению уравнений и неравенств с параметром |
Решение сюжетных, прикладных геометрических задач, на исследование свойств функции, сводящихся к уравнениям и неравенствам |
Следует отметить, что традиционная схема обучения заключается в информировании учащихся об особенностях решения задач и организации деятельности по использованию этой информации. Однако в случае задач с конкретным параметром уточняется только методологическая информация (о критериях успешности, способах решения, условиях выбора управляющих значений и т. д.), а распространяются теоретические сведения и введенная терминология для уравнений и неравенств с одним Переменная. Поэтому здесь предпочтителен иной способ организации обучения, основанный не на усвоении подготовленной информации, а на вдумчивом анализе собственных трудностей и успехов в решении задач. Этот путь определяется спецификой характера методологического познания, которое относится к знанию рефлексивного типа (источником является не восприятие внешней действительности, а сознание внутреннего «Я»).
Психологи и педагоги обратились к категории рефлексивной деятельности относительно недавно в связи с задачами гуманизации образования, усиления его развивающей функции.
Психологи И. Н. Семенов и С. Ю. Степанов показали, что в мышлении можно выделить несколько иерархических уровней, высшими из которых являются уровни интеллектуальной и личностной рефлексии. Рефлексия выполняет в мышлении регулирующую функцию (планирует деятельность, контролирует выполнение программы, диагностирует трудности, корректирует образы и программы), а также интегрирующую функцию: помогает выявить и обобщить знания, содержащиеся в опыте. Именно вторая функция рефлексии делает эту деятельность воспитательно значимой.
Рефлексивные механизмы включаются только при интеллектуальных затруднениях, поэтому включение учащихся в рефлексивную деятельность необходимо начинать с осознания проблемы. Реализацию данного положения предлагается осуществлять по следующей схеме.
— Учитель предъявляет учащимся проблемную ситуацию, связанную с анализом их деятельности или оценкой результатов деятельности учителя.
— Учитель обсуждает с учащимися параметры анализа, демонстрирует круг возможных направлений осуществления действий, критерии их дорогой.
— Учитель дает учащимся возможность самостоятельно принимать решения.
Литература:
- Виноградова, Л. В. Методика преподавания математики в средней школе [Текст] / Л. В. Виноградова- Ростов н/д: Феникс, 2005.- 252с..
- Голубев, В. И. О параметрах — с самого начала [Текст] / В. И. Голубев, А. М. Гольдман, Г. В. Дорофеев // Репетитор. — 2007. — № 2 — с. 3–13..
- Котухов, С. К. Различные способы решения задач с параметрами [Текст] // Мат. в шк.- 1998.-№ 6.- С. 9–12..
- Колягин, Ю. М. Методика преподавания математики в средней школе: общая методика [Текст]: учеб. пособие для студентов физико- математических факультетов пед. институтов.- М.: Просвещение, 1975.- 462с..
- Леонтович, А. В. Исследовательская деятельность школьников [Текст] / / Школьные
- Пронина, Е. С. Линейные уравнения с параметрами: методические рекомендации [Текст] // Мат. в шк.- 2000. -№ 12.- С.3–5..
- Савенков, А. И. Исследовательская деятельность учащихся [Текст] // Школьные технологии.- 2008.- № 1.- С. 11- 20. 21.
- Цыпкин, А. Г. Справочник по методам решения задач по математике для средней школы [Текст] / А. Г. Цыпкин, А. И. Пинский. — 2-е издание, перераб. и доп. — М.: Наука, 2009. — 576 с..
- Шахмейстер, А. Х. Уравнения и неравенства с параметрами [Текст]/ А. Х. Шахмейстер.-М.: Виктория плюс, 2010,-136с..
- Шерстаков, С. В. Уравнения с параметром [Текст] / С. В. Шерстаков, Е. Н. Юрченко.- М.: Слог,1993.- 107с.. Шихалиев, Х. Ш. Уравнения и неравенства с параметрами [Текст] // Мат. в шк.- 1980.-№ 21.- С. 34- 35..
- Ястребинецкий, Г. А. Задачи с параметрами [Текст] / Г. А. Ястребинецкий.- М.: Просвещение, 2006.- 128с.







