Для выполнения поверки координатно-измерительных машин (КИМ) в соответствии с методикой [1] необходимо закреплять концевые меры длины в рабочем пространстве КИМ в различных положениях. При применении мер длиной до 0.5 метра для этой цели используется сварной или цельнометаллический треугольник с отверстиями, закреплённый в необходимом положении на столе КИМ, и на который устаналиваются меры. Такая конструкция является очень жёсткой и широко используемой при проведении поверок КИМ.
Согласно методике поверки [1] необходимо, чтобы длина концевой меры составляла не менее 0.8 от максимальной длины рабочего пространства КИМ. Т.е. при поверке больших координатно-измерительных машинах возникает необходимость применения концевых мер длины свыше 0.5 метра, что приводит к сложностям использования и невозможности использования вышеописанного приспособления.
В данной статье выполнен анализ деформации приспособления под действием усилия, возникающего при ощупывании концевой меры длины, закреплённой в приспособлении, на координатно-измерительной машине. Схема нагружения представлена на рисунке 1.
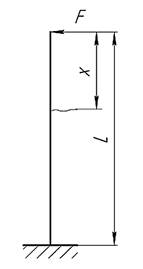
Рис. 1: Схема.
2 Уравнение прогиба стержня приспособления
Определим прогиб стержня, жёстко закреплённого одним концом, под действием силы F перпендикулярной его оси. Для этого запишем формулу Эйлера [3, стр.276]:
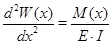 (1)
(1)
В данном случае 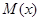 =
= 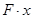 , где x - координата вдоль оси стержня (рис. 1). Для нахождения прогиба подставим
, где x - координата вдоль оси стержня (рис. 1). Для нахождения прогиба подставим 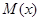 в (1) и дважды проинтегрируем по
в (1) и дважды проинтегрируем по 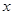 . После первого интегрирования получим:
. После первого интегрирования получим:
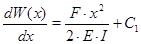
После второго интегрирования уравнение примет вид:
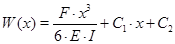
По рис.1 задаём граничные условия 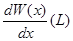 =
=  и
и 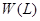 =
=  и находим значения констант
и находим значения констант 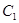 и
и 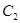 :
:
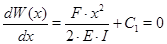
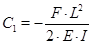
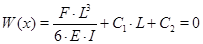
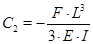
Окончательно формула прогиба примет следующий вид:
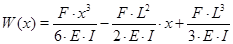
Прогиб у вершины стержня, в точке приложения силы, будет равен:
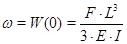 (2)
(2)
В качестве материала стержня возможно применение стали и алюминия. Справочные значения модулей упругости приведены в таблице 1.
Таблица 1: Модули упругости
|
Материал |
Модуль упругости, Е, |
|
Сталь |
|
|
Алюминий |
|
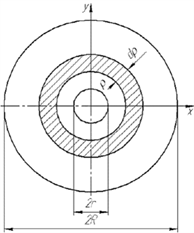
Рис. 2: Сечение.
Рассмотрим кольцевое сечение стержня рис.2, с наружным и внутренним радиусами 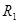 и
и 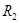 . Сначала определим полярный момент инерции для произвольного сечения радиусом
. Сначала определим полярный момент инерции для произвольного сечения радиусом 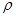 и шириной
и шириной 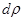 по формуле [2, стр.112]:
по формуле [2, стр.112]:
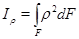 (3)
(3)
Принимая во внимание, что площадь 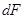 можно представить в следующем виде:
можно представить в следующем виде:
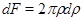
получим следующую формулу для вычисления полярного момента инерции:
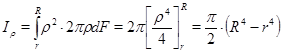
Для определения осевого момента инерции воспользуемся зависимостью: 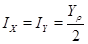 . Окончательной будем иметь:
. Окончательной будем иметь:
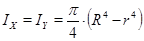 (4)
(4)
Частным случаем является использование стержня сплошного сечения (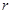 =
=  ), тогда формула (4) примет вид:
), тогда формула (4) примет вид:
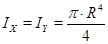
Произведём расчёт прогибов стержней различной формы сечения и изготовленных из различного материала. Рассмотрим четыре случая: два различных сечения изготовленные из двух различных материалов.
Примем 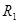 =
= 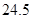 мм,
мм, 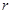 =
= 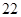 мм. Подставляя эти величины в формулу (2) вычислим прогибы кольцевого стержня различной высоты. Результаты приведены в таблицах 2 и 3.
мм. Подставляя эти величины в формулу (2) вычислим прогибы кольцевого стержня различной высоты. Результаты приведены в таблицах 2 и 3.
Таблица 2: Кольцевое сечение. Материал - сталь.
|
Высота стержня ( |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Прогиб ( |
<0.01 |
0.03 |
0.09 |
0.22 |
0.42 |
0.73 |
1.15 |
1.72 |
2.45 |
3.37 |
Таблица 3: Кольцевое сечение. Материал - алюминий.
|
Высота стержня ( |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Прогиб ( |
<0.01 |
0.08 |
0.26 |
0.62 |
1.20 |
2.08 |
3.30 |
4.93 |
7.01 |
9.62 |
Примем 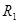 =
= 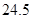 мм,
мм, 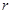 =
=  мм. Подставляя эти величины в формулу (2) вычислим прогибы сплошного стержня различной высоты. Результаты приведены в таблицах 4 и 5.
мм. Подставляя эти величины в формулу (2) вычислим прогибы сплошного стержня различной высоты. Результаты приведены в таблицах 4 и 5.
Таблица 4: Сплошное сечение. Материал - сталь.
|
Высота стержня ( |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Прогиб ( |
<0.01 |
<0.01 |
0.03 |
0.08 |
0.15 |
0.25 |
0.40 |
0.60 |
0.86 |
1.18 |
Таблица 5: Сплошное сечение. Материал - алюминий.
|
Высота стержня ( |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Прогиб ( |
<0.01 |
0.03 |
0.10 |
0.22 |
0.42 |
0.73 |
1.15 |
1.72 |
2.45 |
3.37 |
Алюминиевый стержень кольцевого сечения имеет слишком большие значения прогиба и дальнейшее его рассмотрение в качестве основы для приспособления для закрепления концевых мер нецелесообразно.
Построим график (рис.3), характеризующий зависимость величины прогиба от высоты стержня. Для наглядности на графике прямыми линиями показана величина погрешности координатно-измерительной машины Carl Zeiss PRISMO 10 S-ACC (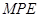 =
= 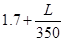 мкм) (верхняя прямая) и
мкм) (верхняя прямая) и 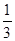 этой величины (нижняя прямая).
этой величины (нижняя прямая).
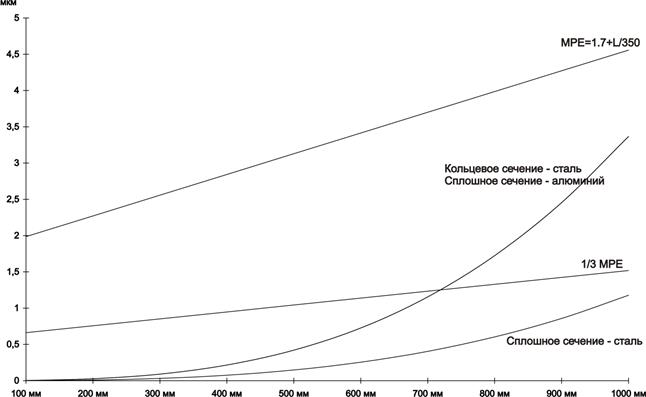
Рис. 3: Зависимость величины прогиба от длины стержня.
Список литературы
[1] МИ 2569-99 Машины координатно-измерительные портального типа. Методика поверки. Всероссийский Научно-Исследовательский Институт Метрологической Службы (ВНИИМС) Госстандарта России, Москва, 1999.
[2] Александров А.В, Потапов В.Д, Державин Б.П. Сопротивление материалов. М.: Высшая школа, 1976 г.
[3] Беляев Н.М. Сопротивление материалов. М.: Наука, 1976 г.
[4] Выгодский М.Я. Справочник по высшей математике. М.: АСТ, 2008. 992с.
[5] Голубев Э.А. Сопоставление различных подходов к оценке неопределённости измерений. // Измерительная техника. №3, 2008. С. 6-9
[6] Estler W.T., Phillips S.D., Borchardt B., Hopp T., Witzgall C., Levenson M., Eberhardt K., McClain M., Shen Y., Zhang X. Error compensation for CMM touch trigger probes. // Precision Engineering. Vol. 19, №2, October 1996, pp. 85-97(13).
[7] Cauchick-Miguel P.A., King T.G. Factors which influence CMM touch trigger probe performance. // International Journal of Machine Tools and Manufacture. Vol. 38, №4, March 1998, pp. 363-374(12).
[8] Wo niak A., Dobosz M. Metrological feasibilities of CMM touch trigger probes. Part I: 3D theoretical model of probe pretravel. // Measurement. Vol. 34, Issue 4, December 2003, pp. 273-286.
niak A., Dobosz M. Metrological feasibilities of CMM touch trigger probes. Part I: 3D theoretical model of probe pretravel. // Measurement. Vol. 34, Issue 4, December 2003, pp. 273-286.
[9] Wo niak A., Dobosz M. Metrological feasibilities of CMM touch trigger probes. Part II: Experimental verification of the 3D theoretical model of probe pretravel. // Measurement. Vol. 34, Issue 4, December 2003, pp. 287-299.
niak A., Dobosz M. Metrological feasibilities of CMM touch trigger probes. Part II: Experimental verification of the 3D theoretical model of probe pretravel. // Measurement. Vol. 34, Issue 4, December 2003, pp. 287-299.







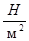
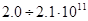
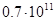
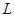 ), мм
), мм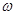 ), мкм
), мкм