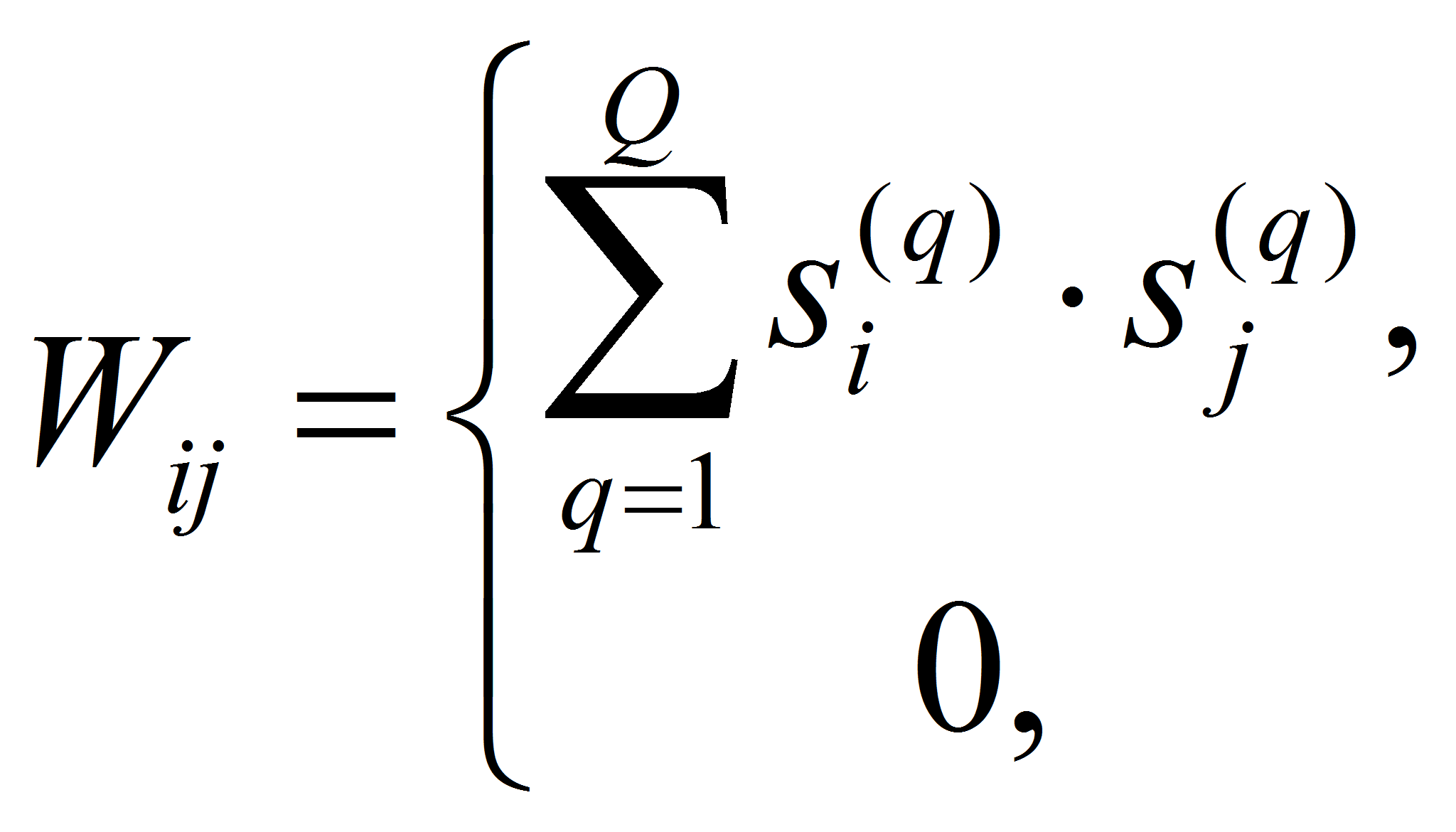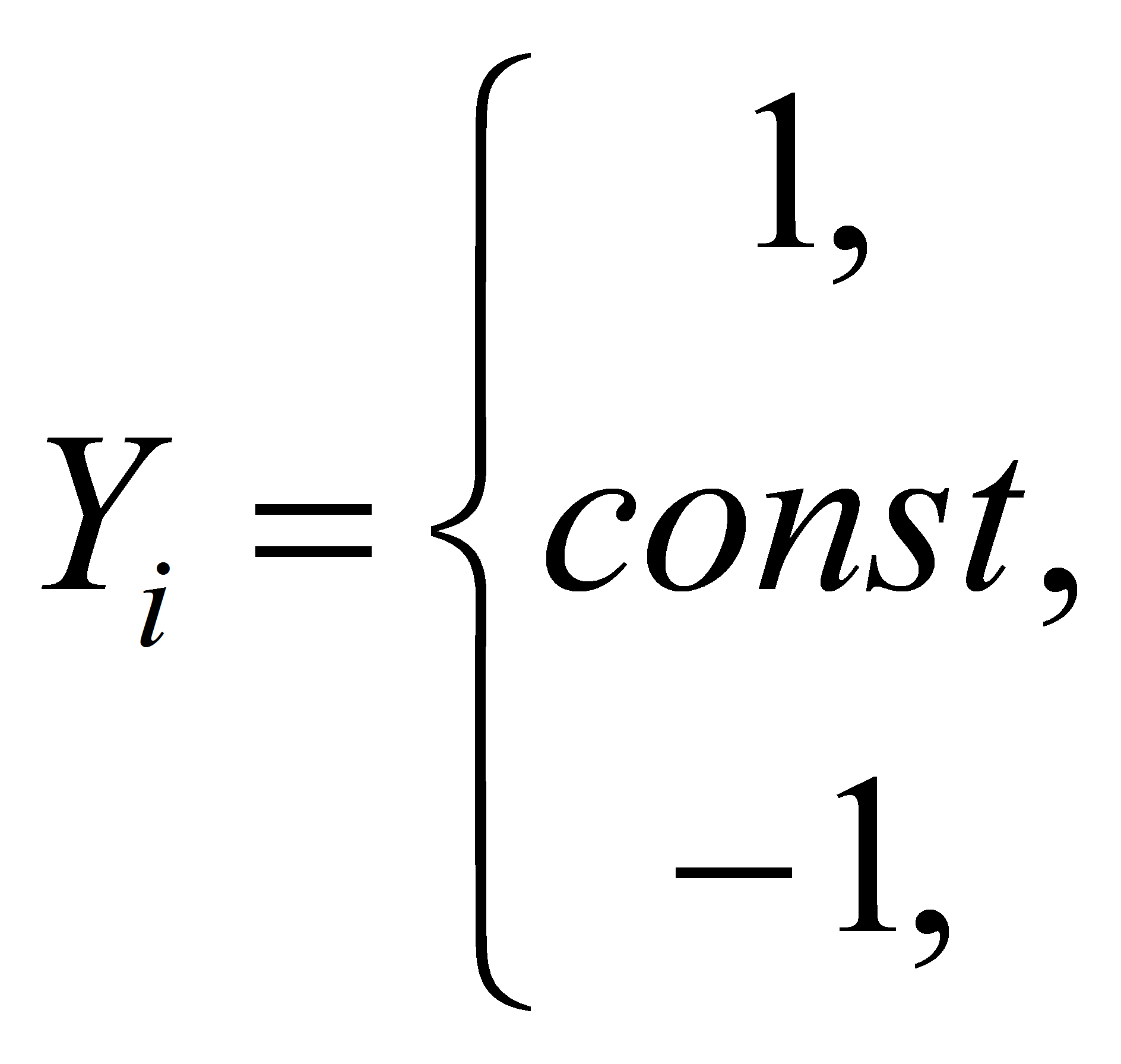Программная реализация сети Хопфилда для распознавания и классификации электрических сигналов

В настоящее время нейронные сети широко используются для решения трудно формализуемых задач, то есть таких, которые не имеют явного алгоритма. Одной из них является задача распознавания и классификации образов. Для ее решения часто используют классическую полносвязную нейронную сеть прямого распространения (многослойный персептрон), для обучения которого используется алгоритм обратного распространения ошибки. Этот алгоритм заключается в распространении сигналов ошибки от выходов сети к ее входам в направлении, обратном прямому распространению сигнала в обычном режиме работы. Таким образом, осуществляется корректировка весов сети. Однако эти сети обладают такими недостатками, как:

• длительность обучения;

• подбор правильной размерности сети.

Длительность обучения персептрона прямо пропорциональна числу синапсов. Если сеть полносвязная, значит выход нейрона предыдущего слоя связан с входом каждого нейрона последующего слоя. Таким образом, если имеется входной образ размерностью 1000х1, то первый слой должен содержать 1000 нейронов. Также в настоящее время не существует универсальных алгоритмов для того чтобы вычислить минимальное необходимое число нейронов в каждом слое. При достаточно большой размерности входного образа не следует использовать персептрон, так как в нашем случае потребуется использовать скрытый слой нейронов, размерность которого будет еще выше, что уменьшит скорость обучения сети. Кроме того, слишком простые сети могут не запомнить достаточное число образов, а погрешность сложных сетей будет велика за счет эффекта «насыщения», то есть при решении сеть не сможет достигнуть глобального минимума. В связи с этим логичнее будет использовать нейронную сеть Хопфилда.

Аналогия физической памяти с искусственной сетью

Нейронная сеть Хопфилда является разновидностью упрощенной модели человеческого мозга. Механизм ассоциативной памяти достигается за счет обратных связей. Задача, решаемая этой сетью в качестве ассоциативной памяти, заключается в следующем: на вход сети поступает кортеж, состоящий из последовательности мгновенных значений напряжения, снятых при помощи мультиметра Agilent 3440А через равные промежутки времени. Число этих значений, к примеру, равно 1000. В зависимости от входного сигнала сеть должна вспомнить по частичной неискаженной информации ближайший образ.

Описание и обучение сети

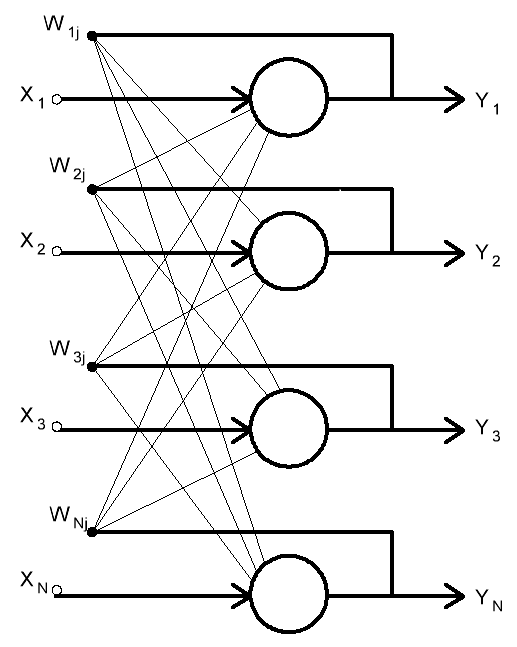
Рассмотрим параметры реализации сети Хопфилда (рис. 1), используемой для нахождения схожих образов между собой.

Сеть состоит из следующих элементов:

Набора исходных шаблонов s^(q)_, где q = 1, … , Q – число этих шаблонов. В нашем случае |Q| = 40.

Данная сеть является полносвязной, то есть выход каждого нейрона связан с входом всех остальных нейронов, кроме самого себя. Также сеть является однослойной, где в качестве входов и выходов используются одновременно одни и те же нейроны. Выходные импульсы нейронов можно обозначить, как Y_i, i = 1, … , N. N – число нейронов, которое соответствует размерности обучающих векторов.

Рис 1. Структура сети Хопфилда

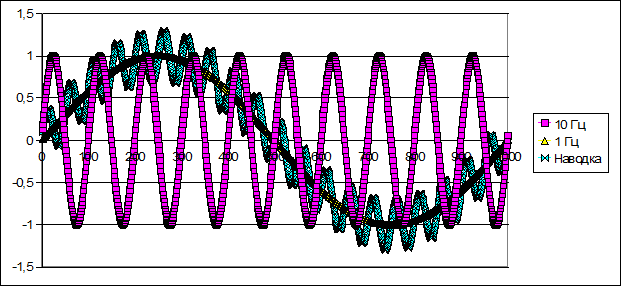
В работе использован вектор длиной 1000 элементов. Обучающие векторы хранятся в обычных текстовых файлах. Они содержат последовательность идеальных мгновенных значений периодических синусоидальных, прямоугольных, треугольных, трапецеидальных сигналов в диапазоне частот от 1 до 100 Гц с шагом 10 Гц. Значения выровнены относительно амплитуды сигнала для того, чтобы она не влияла на процесс принятия решения. Так как для сигналов с разной частотой вектор имеет одинаковую длину, а скорость снятия данных вольтметром постоянна, то чем большую частоту имеет сигнал, тем больше периодов помещается в векторе. Для ясности на Рис 2 приведен график, на котором изображены идеальные сигналы частотой 1 Гц, 10 Гц. Сигнал с частотой 1 Гц промодулирован другим синусоидальным сигналом с частотой 50 Гц (к примеру, наводка от сети). Амплитуда этой наводки – 30 % от амплитуды самого сигнала.

Рис.2. Пример образцовых и зашумленного образов

Распознавание неизвестного образа заключается в сведении его к одному из известных. Для того, чтобы это было возможно, сеть необходимо обучить. Обычно сеть Хопфилда обучается при помощи правила Хебба: то есть создается матрица весов W_ij, представляющая из себя кортеж (вектор), в нашем случае размерностью 1000x1000. Особенностью данной матрицы является то, что она симметрична относительно главной диагонали. Это является одним из необходимых, но не достаточных условий для достижения стабильной работы сети. Также все элементы главной диагонали равны нулю (W_ii = 0). Это связано с тем, что выход i-го нейрона не поступает на его вход. Перед началом работы сети необходимо задать значения всем элементам вектора W. Для этого можно использовать правило Хэбба для двуполярных векторов:

если i ≠ j

если i = j

Здесь i,j – элементы из обучающей выборки. Таким образом, W_ij формируют соответствующие элементы, последовательно поступающие из матриц известных шаблонов.

Работа сети

После того как матрица W сформирована можно подавать на вход сети искаженный образ. Размерность этого вектора должна соответствовать векторам из обучающей выборки. Вектор Х одновременно попадает на выходы всех нейронов. Тут стоит упомянуть о том, что сеть может работать в двух режимах: синхронном и асинхронном. Различие заключается в том, что при синхронном режиме работы сети активационная функция каждого нейрона рассчитывается без учета выходных значений других нейронов (активационные функции всех нейронов рассчитываются в один момент времени). Следовательно, их выходные значения формируются одновременно. Недостатком этого подхода является то, что существует вероятность появления бесконечного чередования двух состояний (то есть динамического аттрактора).

Более продуктивным является асинхронный режим работы сети. Во время его работы произвольно выбирается нейрон и для него рассчитывается активационная (передаточная) функция:

если Y_i > Θ_i

если Y_i = Θ_i

если Y_i < Θ_i

В качестве функции активации используется обычная пороговая функция с порогом Θ = 0. В качестве передаточной можно использовать более сложные функции, такие как сигмоидальные и тангенциальные, но изменения будут несущественны.

После расчета активационной функции выходное значение нейрона может измениться. С учетом этого изменения рассчитывается активационная функция для следующего нейрона. Это продолжается до тех пор, пока сеть не достигнет устойчивого состояния - то есть пока выходные значения нейронов не будут изменяться. Если же состояние равновесия не будет достигнуто за заданное число итераций (в нашем случае 2500), то образ считается нераспознанным.

Вывод

В результате была разработана программная реализация сети Хопфилда на языке программирования Python 3.2, успешно распознающая искаженные/зашумленные входные сигналы и сводящая их к одному из известных заранее. Отношение сигнал/шум, при котором программа не испытывает трудностей в распознавании составляет 3:1. Это отношение прямо пропорционально размерности обучающих векторов (и соответственно искаженного вектора).

К достоинствам сети Хопфилда можно отнести:

• относительно простую реализацию;

• быструю скорость обучения;

• большую масштабируемость.

Недостатком сети является малый объем памяти. Максимальное число шаблонов, можно рассчитать по следующей формуле:

, где N – число нейронов в сети.

Если не придерживаться этого соотношения, сеть выдаст некий собирательный образ, в состав которого будут входить несколько исходных.

В статье преднамеренно опущено подробное описание кода программы, чтобы не нарушать целостность описания алгоритма работы сети. Соответствующие комментарии приведены непосредственно в самом коде.

Литература:

1. С. Короткий Нейронные сети Хопфилда и Хэмминга.

2. Саймон Хайкин Нейронные сети. Полный курс. 2-е издание.

3. Яхъяева Г. Э. Нечеткие множества и нейронные сети. Учебное пособие.

4. Mark Pilgrim. Dive into Python 3.

Исходный код программы:

Основной модуль h_main.py

import sys

from parser_and_co import parse, parse_image, print_image, DIMENSION

from h_net import h_net

learnt_images = "learnt_images"

unfamiliar_image = "unfamiliar/unfamiliar.txt"

def main(argv):

images_ll = parse(learnt_images)

image_l = parse_image(unfamiliar_image)

print("Known images")

for i in images_ll:

print_image(i, DIMENSION)

print("Remembering images")

network = h_net(DIMENSION)

for i in images_ll:

network.remember(i)

print()

print("Changed image ")

print_image(image_l, DIMENSION)

print()

print("Detecting image:")

(recognized, recimage, counter) = network.recognize(image_l)

print()

if recognized:

print("Recognized in %g" %counter)

else:

print("Not recognized in %g" %counter)

print_image(recimage, DIMENSION)

if __name__ == '__main__':

main(sys.argv[1:])

Дополнительный модуль, реализующий чтение из файлов и ввод/вывод информации parser_and_co.py:

from __future__ import with_statement

import os

MAX = 1024

DIMENSION = 16

d_parse = {'.': -1, '#': 1}

d_print = {-1:'.' ,1 :'#' }

#

# parse returns a list of symbols from the file

#

def parse(dir):

filenames_l = []

for filename in os.listdir(dir):

filepath = os.path.join(dir, filename)

if os.path.isfile(filepath):

filenames_l.append(filepath)

images_l = []

for filepath in filenames_l:

image = parse_image(filepath)

images_l.append(image)

return images_l

#

# parse_image returns file in a list

#

def parse_image(filepath):

with open(filepath) as f:

temporary = f.read(MAX)

temporary = temporary.replace("\n", "")

temporary = temporary.replace("\r", "")

image_l = []

for i in temporary:

image_l.append(d_parse[i])

if len(image_l) != pow(DIMENSION, 2):

raise Exception("The dimension of images must be %gx%g" % (DIMENSION, DIMENSION))

return image_l

#

# print_image prints an image

#

def print_image (list, size):

c = 0

for i in list:

print(d_print[i], end = ' ')

c += 1

if (c % size == 0):

print()

Дополнительный модуль, описывающий класс нейронной сети, ее методы h_net.py:

import math

import random

from parser_and_co import print_image, DIMENSION

#

# Class of Hopfield net

#

class h_net:

#

# Constructor

#

def __init__(self, dimension):

self.neurons = int(math.pow(dimension, 2)-1)

self.images = []

self.y = [] # keeps the exit variable

self.W = [] # initialization of

r = range(0, self.neurons) # weighted matrix Wij

for i in r: #

self.W.append([0 for i in r]) #

self.queue = list(range(self.neurons))

random.shuffle(self.queue)

#

# Remember according to Hebb's rule

#

def remember(self, image):

self.images.append(image)

r = range(0, self.neurons)

for i in r:

for j in r:

if (i==j):

self.W[i][j] = 0

else:

self.W[i][j] += image[i] * image[j]

#

# Recognize unknown image

#

def recognize(self, image):

counter = 0

self.y = image

j = 0

while (self.images.count(self.y) == 0):

counter +=1

s = 0

for i in range(0, self.neurons):

s += self.W[i][self.queue[j]]*self.y[i] #sum

s += image[self.queue[i]]

s = ((s>10)-(s<10)) # s=(-1) if (s<0); s=1 if (s>0) else s=0

if (s != self.y[self.queue[j]]): # change

self.y[self.queue[j]] = s

print("Image ,while count is ", counter)

print()

print_image(self.y, DIMENSION)

print()

j += 1

if (j == (self.neurons)):

j = 0

if (counter>2500):

return (False, self.y, counter)

return (True, self.y, counter)