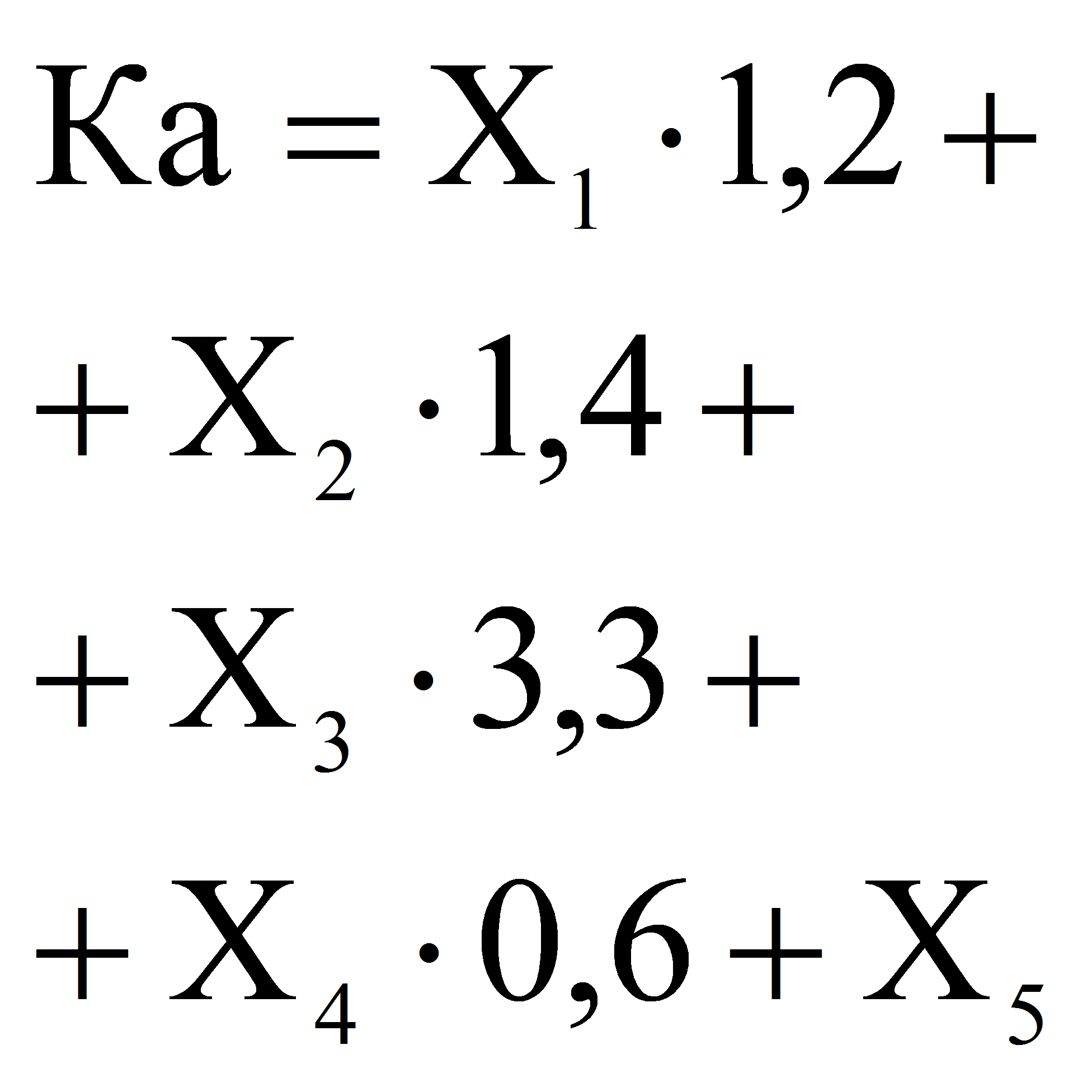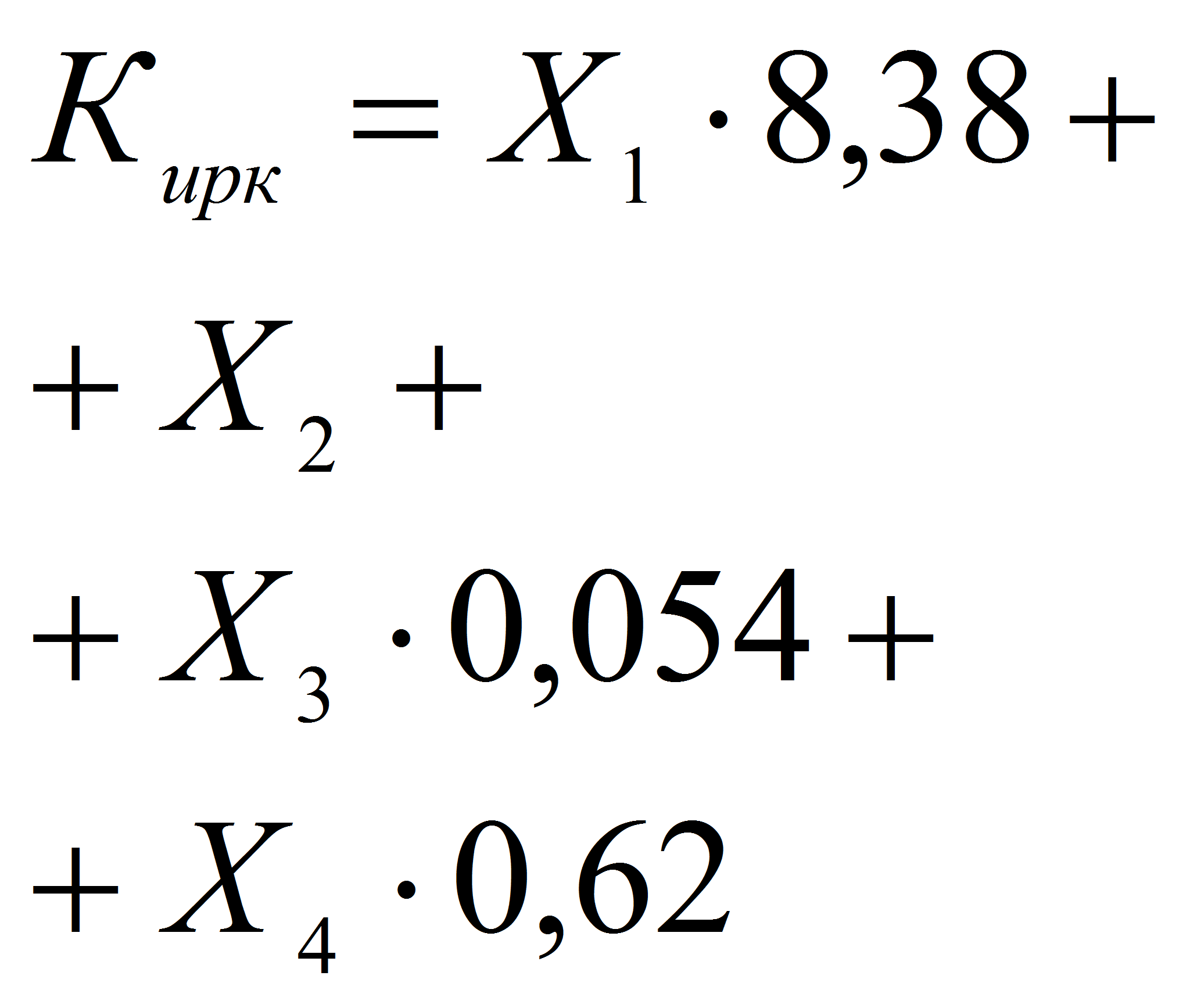Задача определения степени риска банкротства предприятия является актуальной для всех лиц, заинтересованных положением предприятия – руководителя, инвесторов и т.д.
В финансовом анализе хорошо известен ряд показателей, характеризующих отдельные стороны текущего финансово-экономического положения предприятия. И на основе этих показателей были созданы интегральные коэффициенты, характеризующие общее положение и вероятность банкротсва предприятия: Модель Альтмана, Модель Лиса, Модель Таффлера, Модель Иркутской ГЭА), Модель Фулмера.
Современная проблема заключается в том, что, используя сразу несколько из перечисленных моделей на практике, зачастую получается разрозненный результат: по некоторым моделям вероятность банкротства высокая, а по другим – низкая. Целью исследования является получения интегрального показателся риска банкротства предприятия с помощью модели нечетких множеств.
Модель Альтмана
Точность прогноза в этой модели на горизонте одного года составляет 95%, на два года – 83%, что является ее достоинством.
Таблица 1
Расчет риска банкротства предприятия по модели Альтмана
|
Название |
Итоговый коэффициент вероятности банкротства |
Условные обозначения |
Дифференциация по уровням вероятности банкротства |
|
|
Модель Альтмана |
|
|
||
|
высокая |
|||
|
средняя |
|||
|
от 3,0 |
низкая |
|||
Недостаток данной модели заключается в том, что ее по существу можно рассматривать лишь в отношении крупных компаний, которые разместили свои акции на фондовом рынке. Расчет факторов и интегрального показателя в модели Альтмана представлен в таблице 1.
Модель Лиса
Модель Лиса, разработанная им в 1972 году, для предприятий Великобритании представлена в таблице 2.
Таблица 2
Расчет риска банкротства предприятия по модели Лиса
|
Название |
Итоговый коэффициент вероятности банкротства |
Условные обозначения |
Дифференциация по уровням вероятности банкротства |
|
|
Модель Лиса |
0,037 |
Критическое значение |
||
Модель Таффлера
Данная модель рекомендуется для анализа как модель, учитывающая современные тенденции бизнеса и влияние перспективных технологий на структуру финансовых показателей (таблица 3).
Таблица 3
Расчет риска банкротства предприятия по модели Таффлера
|
Название |
Итоговый коэффициент вероятности банкротства |
Условные обозначения |
Дифференциация по уровням вероятности банкротства |
|
|
Модель Таффлера |
От 0,2 |
Неплохие долгосрочные перспективы |
||
|
|
|||
Модель Иркутской ГЭА (таблица 4)
По результатам практического его применения появилась информация о том, что значение R во многих случаях не коррелирует с результатами, полученными при помощи других методов и моделей.
Таблица 4
Расчет риска банкротства предприятия по модели Иркутской ГЭА
|
Название |
Итоговый коэффициент вероятности банкротства |
Условные обозначения |
Дифференциация по уровням вероятности банкротства |
|
|
|
Модель Иркутской ГЭА |
До 0 |
Вероятность банкротства максимальная |
|||
|
От 0 до 0,18 |
Высокая |
||||
|
От 0,18 до 0,32 |
Средняя |
||||
|
От 0,32 до 0,42 |
Низкая |
||||
|
От 0,42 |
Минимальная |
||||
Модель Фулмера (таблица 5) классификации банкротства была создана на основании обработки данных 60 ти предприятий: 30 потерпевших крах и 30 нормально работающих - со средним годовым оборотом в 455 тысяч американских долларов.
Точность прогнозов, сделанных с помощью данной модели на год вперёд – 98 %, на два года – 81 %.
Таблица 5
Расчет риска банкротства предприятия по модели Фулмера
|
Название |
Итоговый коэффициент вероятности банкротства |
Условные обозначения |
Дифференцияция по уровню вероятности банкротства |
|
|
Метод Фулмера |
Кф = 5,528X1+0,212X2+ +0,073X3+1,27X4-0,12X5+2,335X6+0,575X7+1,083X8-3,075Х9 |
X1=Нераспределенная прибыль/Валюта баланса |
H<0
|
Банкротство неизбежно
|
|
X2=Выручка от реализации/Валюта баланса |
||||
|
X3=Прибыль до налог.обл/Валюта баланса |
||||
|
X4=Чистая прибыль/Общий размер задолженности |
||||
|
Х5=Долгосрочные об./Валюта баланса |
||||
|
Х6=Краткосрочные об./Валюта баланса |
||||
|
Х7=Lg(Материальные активы) |
||||
|
Х8=Оборотный капитал/Общая задолженность |
||||
|
Х9=Lg(Приб до нал.обл и упл. %/Проценты к уплате) |
||||
Нечетко-множественная модель прогнозирования риска
План исследования риска банкротсва с помощью нечетких множеств включает следующие этапы:
определение нечётких множеств;
отбор и ранжирование показателей;
построение матрицы соответствия и определение финального значения показателя риска банкротства предприятия.
На первом этапе происходит определение лингвистических переменных и нечетких множеств. Предлагается выделить следующие нечеткие множества:
Лингвистическая переменная G «Риск банкротства» также имеет 5 значений:
G1– нечеткое подмножество «предельный риск банкротства»,
G2– нечеткое подмножество «степень риска банкротства высокая»,
G3– нечеткое подмножество «степень риска банкротства средняя»,
G4– нечеткое подмножество «степень риска банкротства низкая»,
G5– нечеткое подмножество «риск банкротства незначительный».
Для отдельного финансового показателя или показателя управления Хiзадаем лингвистическую переменную Вi «уровень показателя Хi» на следующем терм-множестве значений:
Bi1- подмножество «очень низкий уровень показателя Хi»;
Bi2- подмножество«низкий уровень показателя Хi";
Bi3- подмножество «средний уровень показателя Хi»;
Bi4- подмножество «высокий уровень показателя Хi»;
Bi5- подмножество «очень высокий уровень показателя Хi».
На следующем этапе производится отбор низших показателей, которые предполагается использовать в исследовании. Для анализа банкротства предлагается принять ранее рассмотренные модели анализа риска банкротства предприятия (таблица 6).
Ранжировка показателей
Если система показателей проранжироована в порядке уменьшения их значимости, то вес i-го показателяri необходимо олределять по правилу Фишберна, представленного формулой (1).
Ранжировка показателей для 5 моделей, выстроенных в представленном порядке приведена в таблице 6, при этом в графе «фактеческое значение» ставится значение показателей, полученных при расчете для каждого конкретного предприятия.
Таблица 6
Уровень значимости показателей
|
Модель |
Фактическое значение |
Уровень значимости (удельный вес), ri |
Лингвистическое описание |
|
Альтман |
Ка |
0,333 |
Средняя степень Риска |
|
Таффлер |
Кт |
0,267 |
Низкая степень риска |
|
Лис |
Кл |
0,200 |
Очень высокая степень риска |
|
ИГЭА |
Кирк |
0,133 |
Очень низкая степень риска |
|
Фулмер |
Кф |
0,067 |
Очень низкая степеь риска |
Следующим шагом является построение матрицы фактического распределения значений по нечетким множествам (таблица 7). На данном шаге происходит абстрагирование от числовых значений, полученных с помощью представленных ранее моделей анализа риска банкротства предприятий и переход к нечетким множествам лингвистических переменных.
Таблица 7
Матрица распределения фактических значений по нечетким множествам
|
|
Очень низкий |
Низкий |
Средний |
Высокий |
Очень высокий |
|
Альтман |
|
|
|
|
|
|
Таффлер |
|
|
|
|
|
|
Лис |
|
|
|
|
|
|
ИГЭА |
|
|
|
|
|
|
Фулмер |
|
|
|
|
|
|
Итого |
|
|
|
|
|
В таблице 7 в ячейки, соответствующие значениям лингвистических переменных, полученных с помощью моделей анализа риска, ставится «1». В остальные ячейки ставится «0». Например: коэффициент Альтмана получился равным 2.8, что соответствует средней вероятности банкротства предприятия в течение года, соответственно на пересечении строки «Альтман» и столбца «Средний» ставится единица – остальные ячейки по строки заполняются «нулями».
На следующем этапе определяется интегральный коэффициент вероятности банкротства предприятия, основанный на нечетких множествах (формула (2).
где: gj = 0.9 – 0.2*(j – 1);
g – коэффициент вероятности банкротства нечетких множеств;
j – номер столбца;
i – номер строки;
N – количество факторов;
 –уровень принадлежности носителя Xiнечетким
подмножествам Bj
(сумма
по столбцам).
–уровень принадлежности носителя Xiнечетким
подмножествам Bj
(сумма
по столбцам).
На следующем шаге происходит отнесение полученного интегрального показателя риска банкротсва предприятия к финальному суждению (таблица 8).
Таблица 8
Распределение интегрального показателя риска банкротства предприятия
|
Интервал значений Риска (g) |
Заключение о Финаносовом состоянии предприятия |
|
0 - 0,2 |
Предельный риск банкротства |
|
0,2 - 0,4 |
Степень риска банкротства высокая |
|
0,4 - 0,6 |
Степень риска банротства средняя |
|
0,6 - 0,8 |
Низкая степень риска банкротства |
|
0,8 - 1 |
Риск банкротства незначителен |
Многие исследователи теории нечетких множеств считают, что данный метод зачастую помогает воздержаться от более затратного метода экспертных оценок.
Результатом исследования риска бакротства предприятия становится расчитанный коэффициент, который и будет являться основой для принятия управленческого решения (принятия предупредительных мероприятий и т.д).
Литература:
Гиляровская Л.Т. Экономический анализ: Учебник для вузов / Ред. Л.Т. Гиляровской. – М.: Юнити-Дана, 2010.
Недосекин А.О. Комплексная оценка риска банкротства корпорации на основе нечетких описаний. / Недосекин А.О.– М.: Аудит и финансовый анализ, 3, 2009.
Недосекин А.О., Максимов О.Б. Новый комплексный показатель оценки финансового состояния предприятия/Недосекин А.О.– М.: Аудит и финансовый анализ, 8, 2010.
Недосекин А.О., Максимов О.Б., Павлов Г.С. Анализ риска банкротства предприятия: Методическое указание [электронный ресурс]:http://sedok.narod.ru/
Altman E.I. Further Empirical Investigation of the Bankruptcy Cost Question //Journal of Finance, September 1984, pp. 1067 – 1089.
Altman E.I. personal Internet homepage. –http://pages.stern.nyu.edu/~ealtman/index.html.