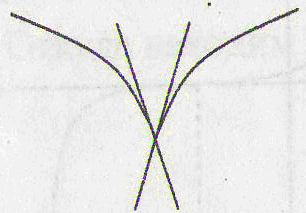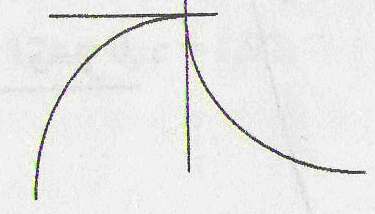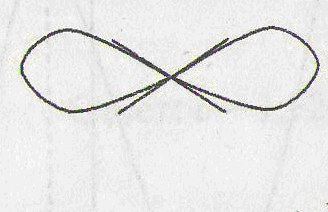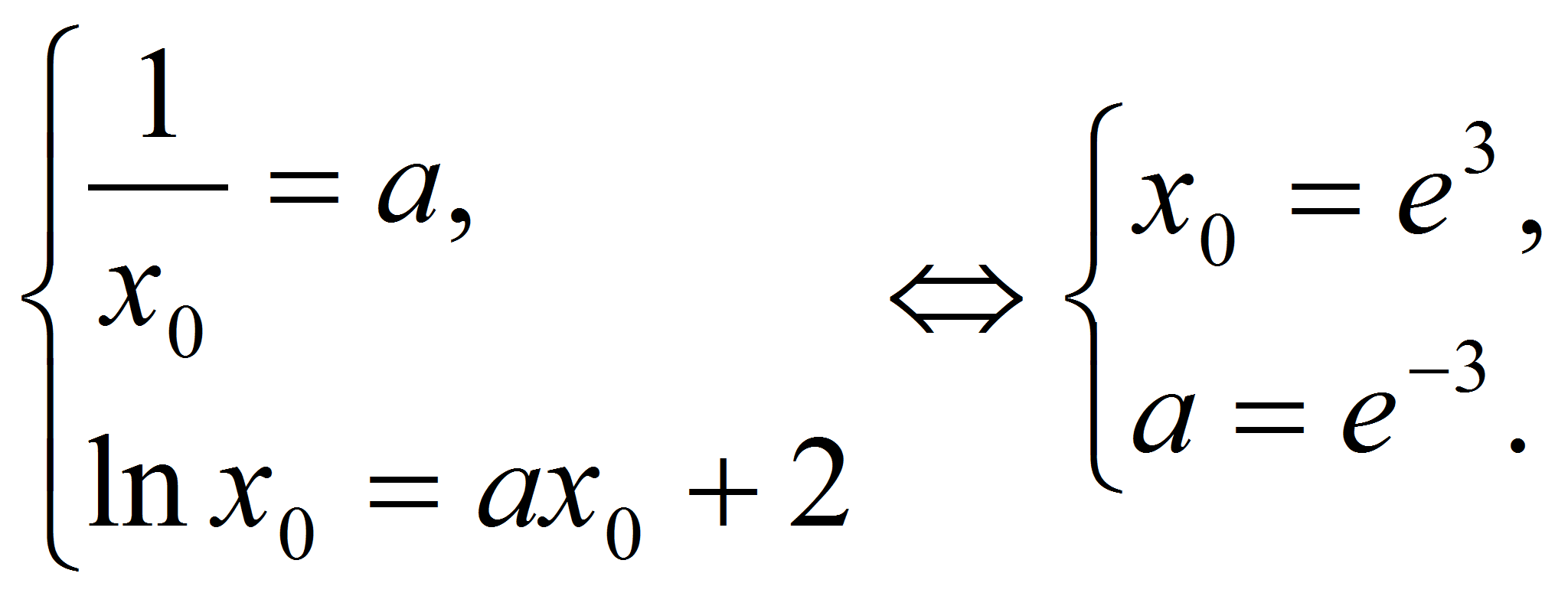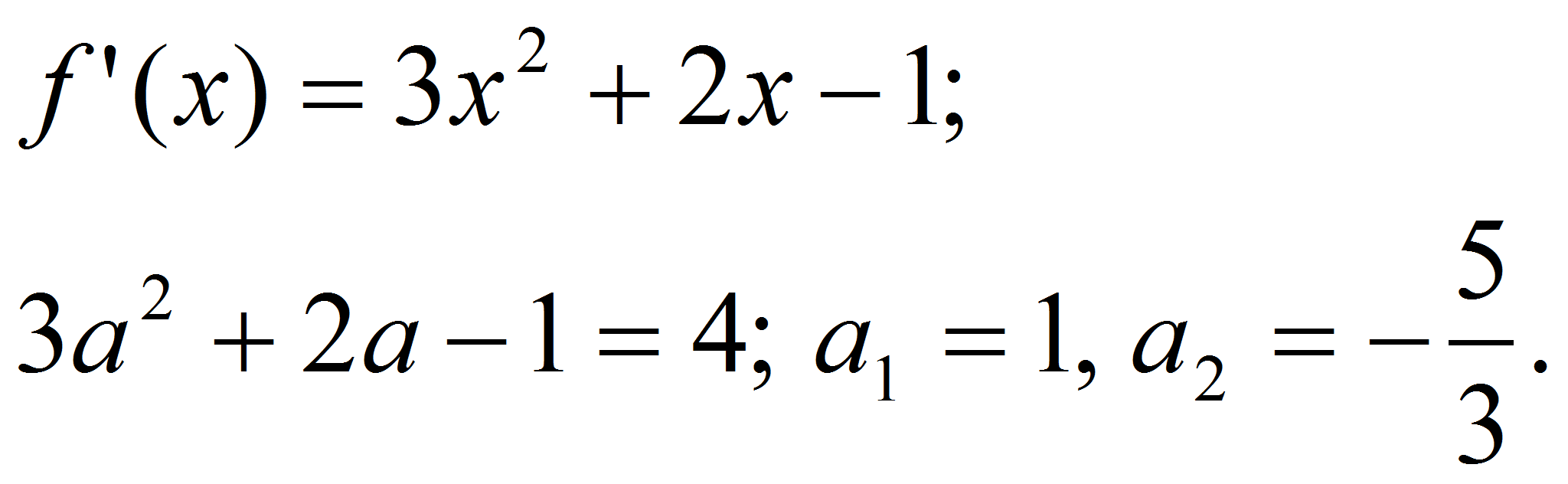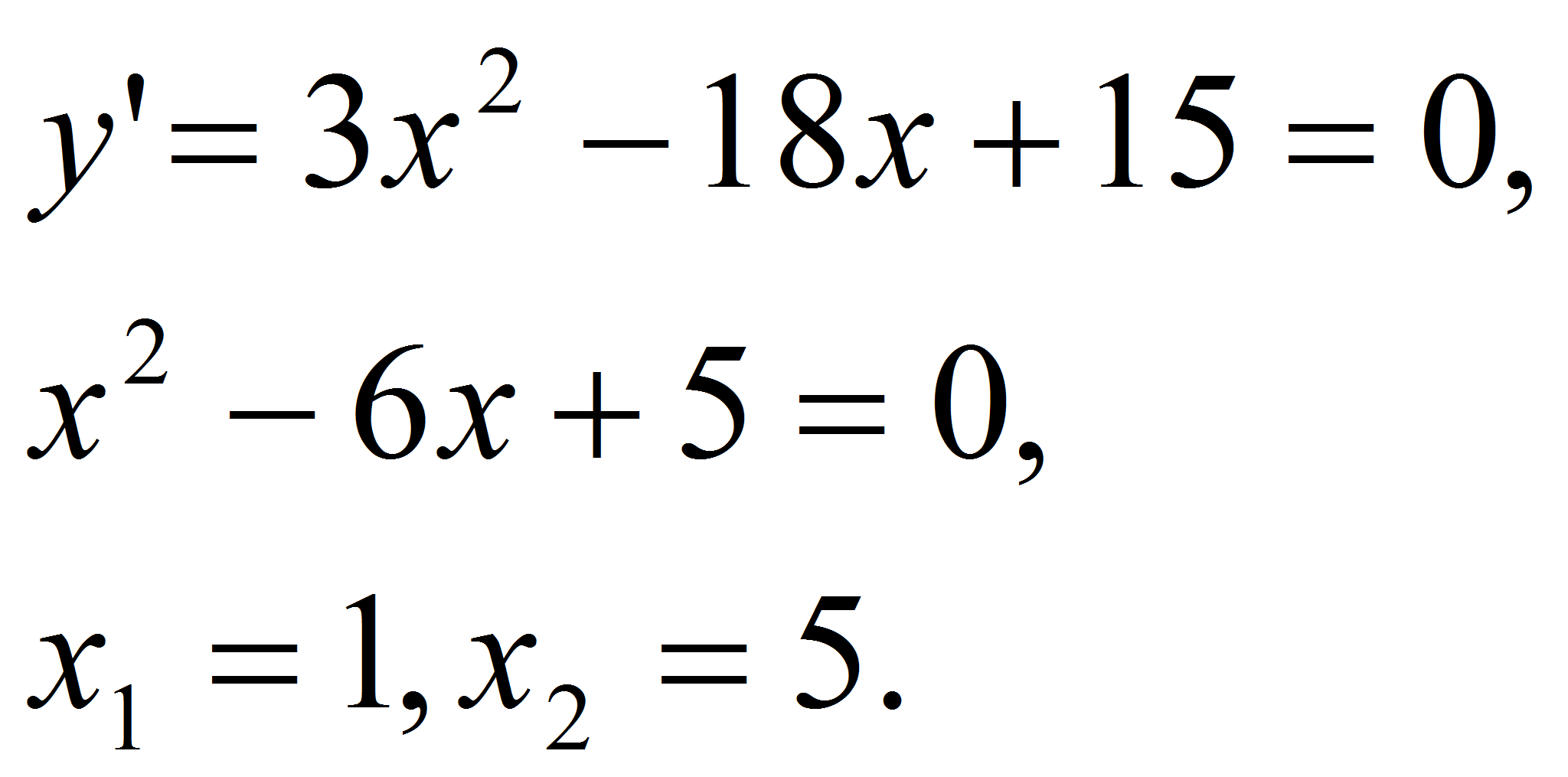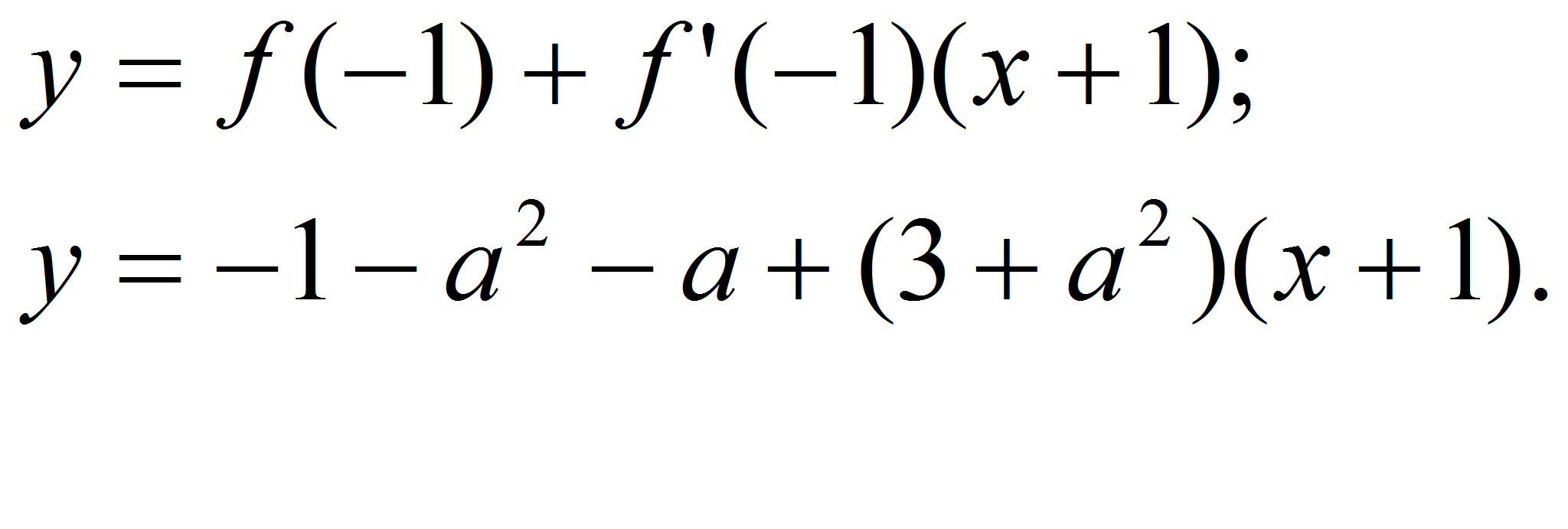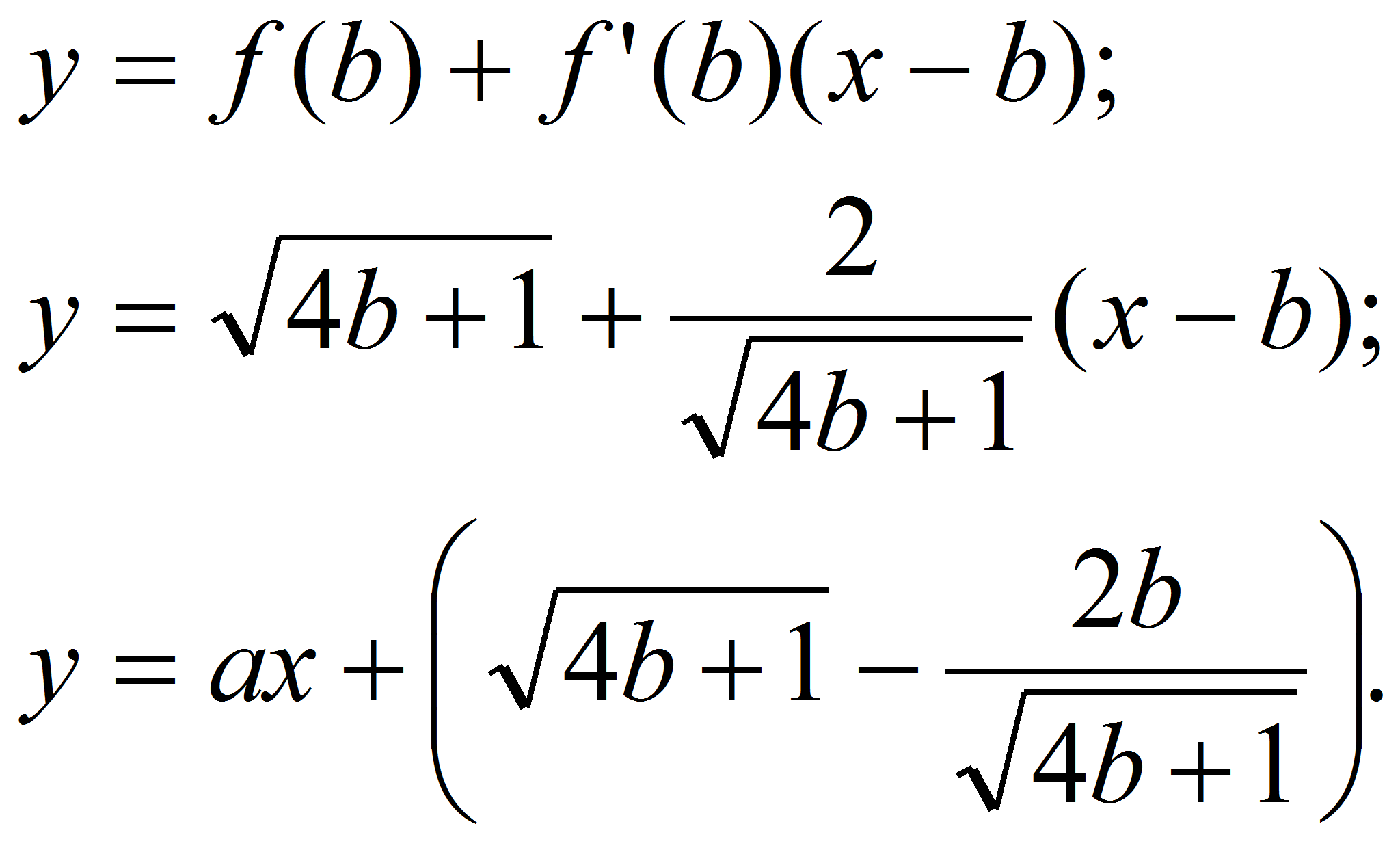Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.
Опр.
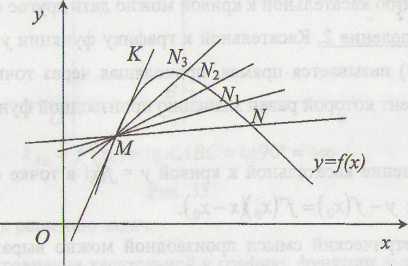
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при
![]()
![]() (рис. 1).
(рис. 1).
Рис. 1
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.
Опр. 2. Касательной к графику функции у = f(x) в точке A0(x0; f(x0)) называется прямая, проходящая через точку A0, угловой коэффициент которой равен значению производной функции у =f(x) в точке с абсциссой x0.
Уравнение
касательной
к кривой у =
f(x)
в точке с
абсциссой х0
имеет вид:
![]() .
.
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
![]() ,
причем ее
угловой коэффициент
равен
,
причем ее
угловой коэффициент
равен
![]() .
Вывод: если в точке х0
есть производная
функции
.
Вывод: если в точке х0
есть производная
функции
![]() ,
то в точке с
этой абсциссой есть касательная к графику
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
![]() и наоборот; если
в точке х0
нет производной
функции
и наоборот; если
в точке х0
нет производной
функции
![]() ,
то в точке с
этой абсциссой нет касательной к графику функции
,
то в точке с
этой абсциссой нет касательной к графику функции
![]() и наоборот.
и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).
угловая точка
точка возврата узловая
точка
![]()
а) б) в) г)
Рис. 2
Рассмотрим решение некоторых задач.
Задачи, связанные с определением того, является ли прямая у = kx + b касательной к графику функции у = f(x). Можно указать два способа решения таких задач.
Находим общие точки графиков, т. е. решаем уравнение f(x) = kx + b, а затем для каждого из его решений вычисляем
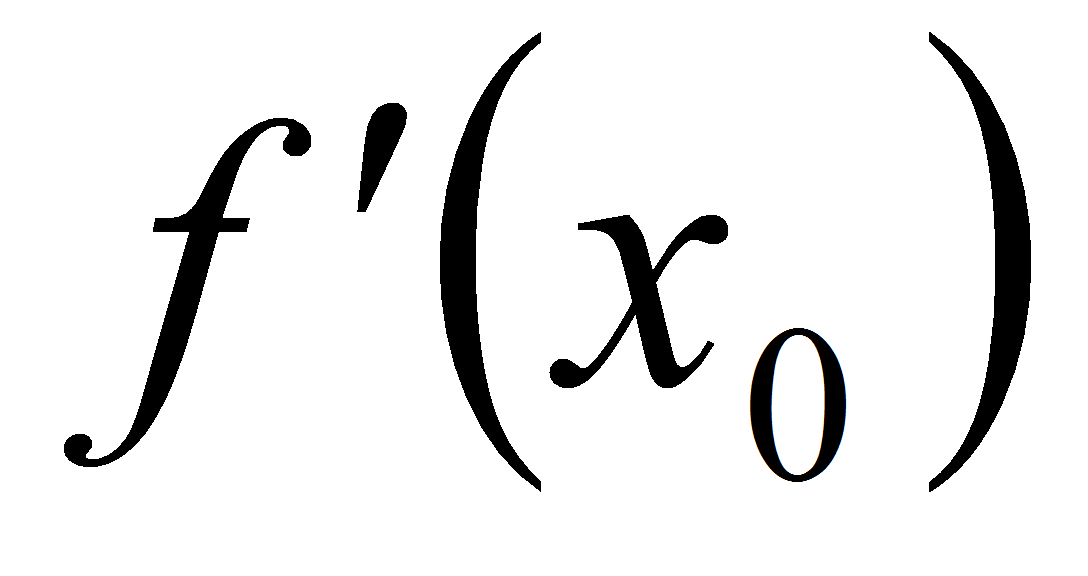 .
В тех случаях, когда
.
В тех случаях, когда
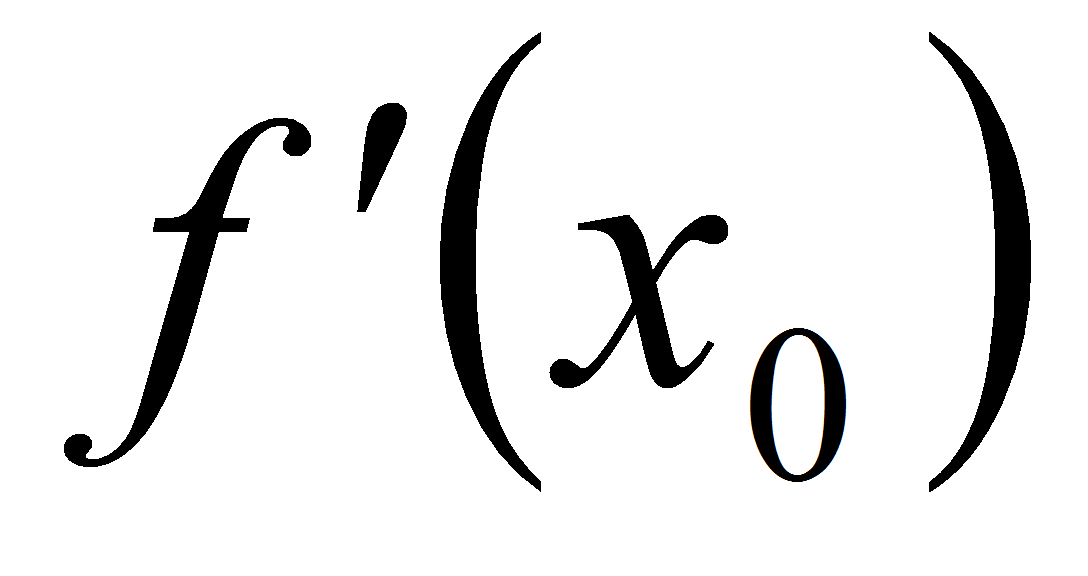 = k,
имеет место касание, в других —
пересечение.
= k,
имеет место касание, в других —
пересечение.Находим корни уравнения
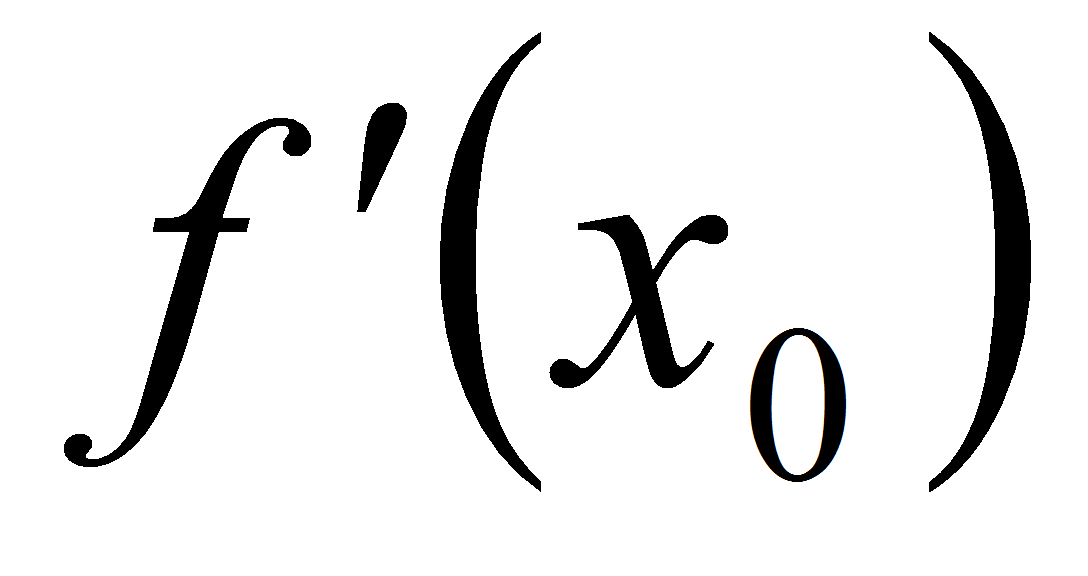 = k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
![]()
Решение.
Записав условие касания
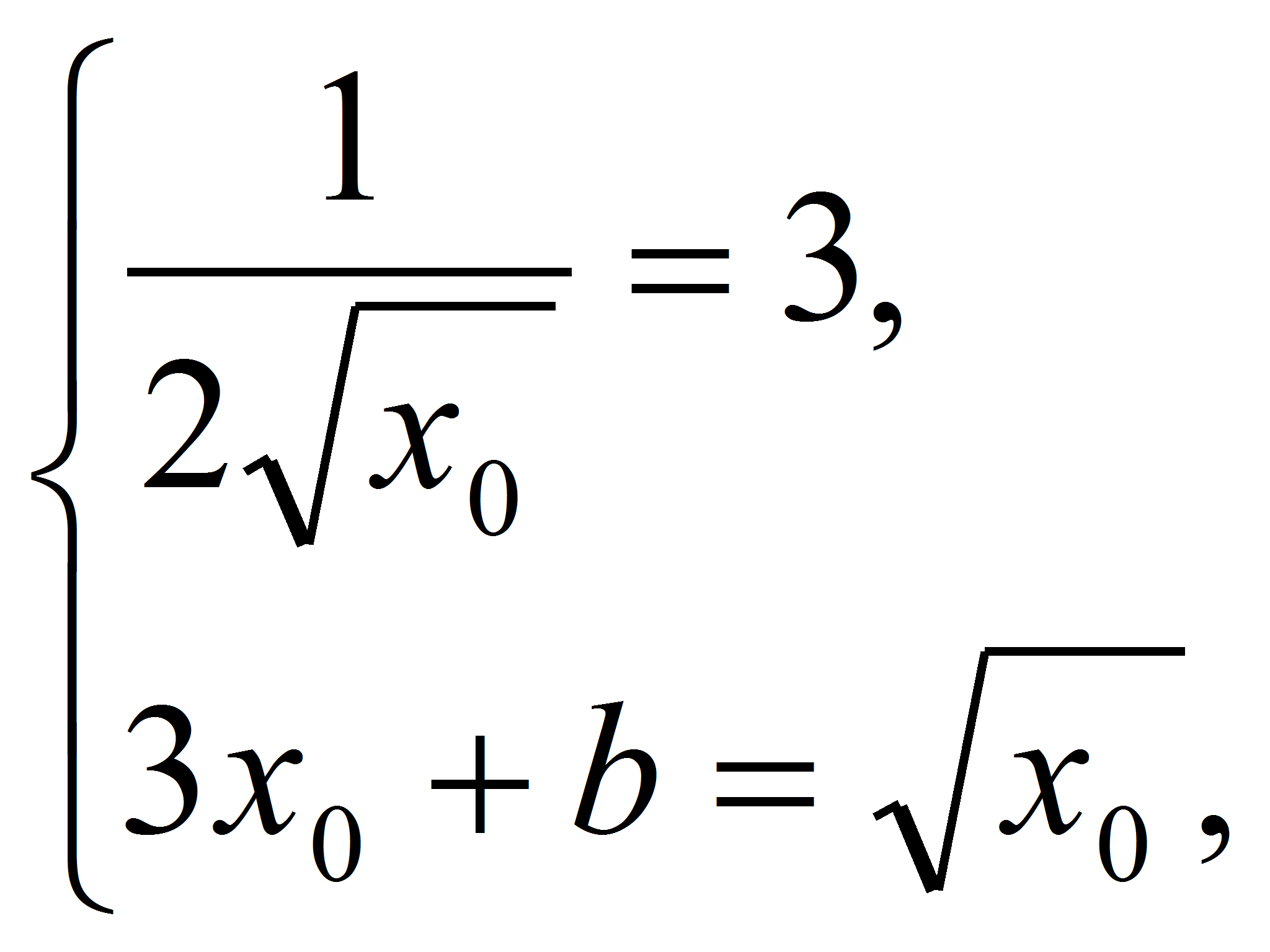 получим
получим
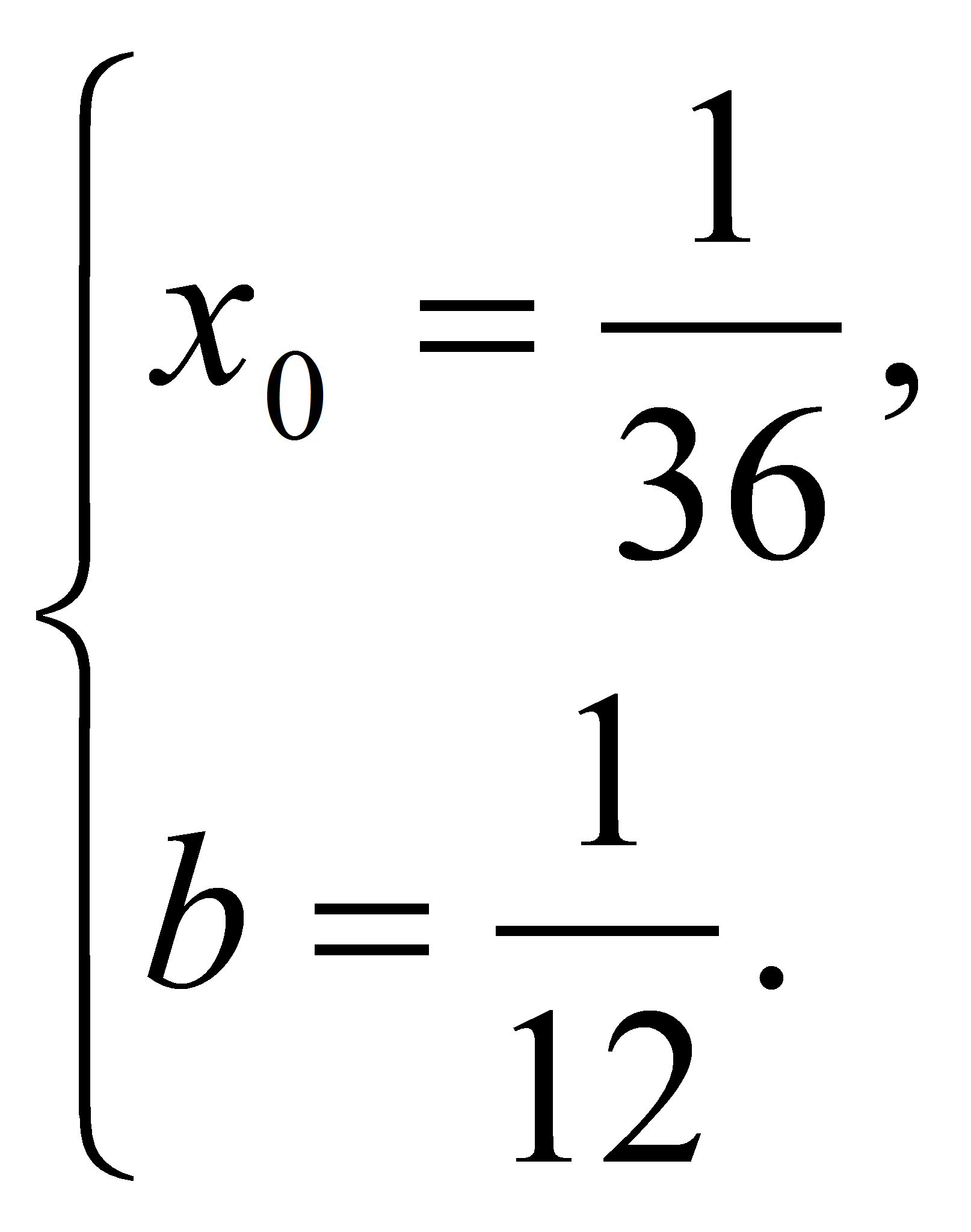
Указание.
Ответ: а = e-3
Указание.
Ответ: а = 7 или а = -1.
Является ли прямая
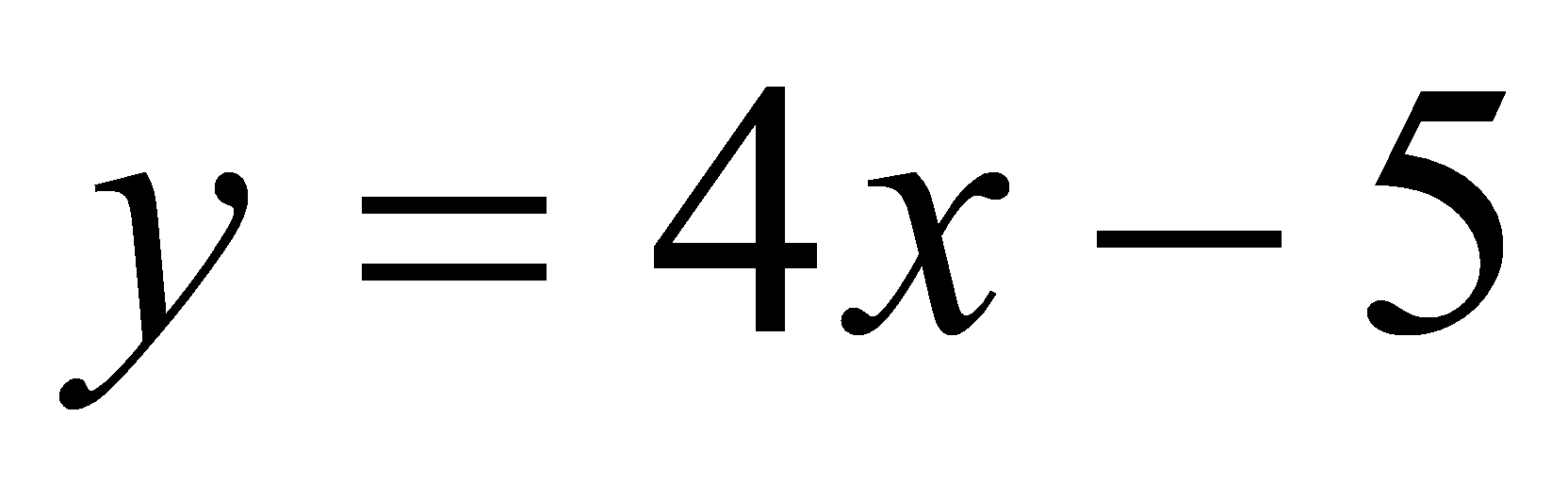 касательной к графику функции
касательной к графику функции
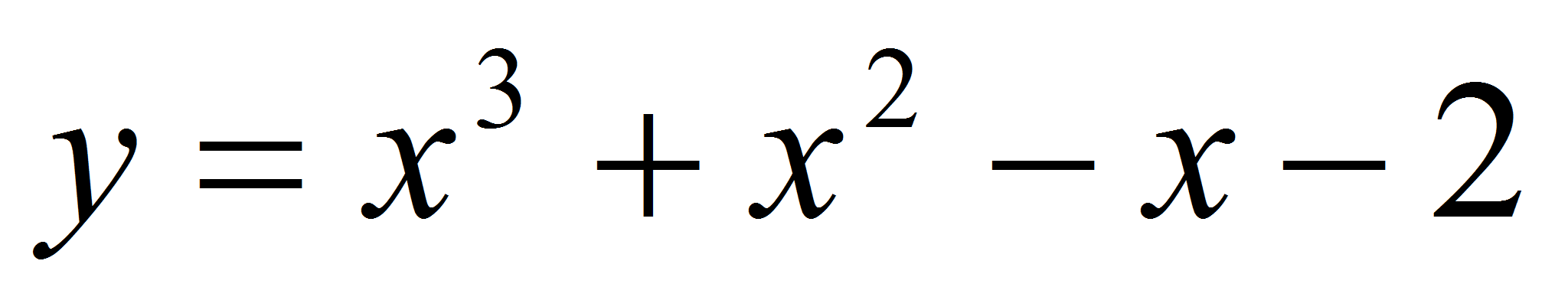 ?
Если является, то найти координаты точки касания.
?
Если является, то найти координаты точки касания.
Решение.
Пусть
![]() .
Из условия следует, что должны выполняться равенство
.
Из условия следует, что должны выполняться равенство
![]() ,
где
,
где
![]() -
возможная абсцисса точки касания. Имеем:
-
возможная абсцисса точки касания. Имеем:
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
![]() как раз и получится
как раз и получится
![]() .
Значит, точка касания имеет координаты (1;-1).
.
Значит, точка касания имеет координаты (1;-1).
Решение.
![]() .
Абсцисса интересующей нас точки касания удовлетворяет уравнению
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
![]() .
Имеем:
.
Имеем:
Таким образом,
![]() .
Значит,
.
Значит,
![]() -
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
-
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
Ответ: 1.
Решение.
Так как касательная должна быть параллельна прямой
![]() ,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
![]() .
Отсюда
.
Отсюда
![]() или
или
![]()
![]() .
Далее составляем уравнение касательной для каждой точки.
.
Далее составляем уравнение касательной для каждой точки.
Найти все значения
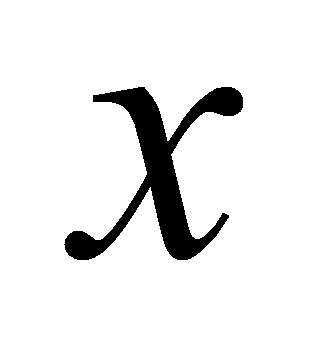 ,
при каждом из которых касательная к графикам функций
,
при каждом из которых касательная к графикам функций
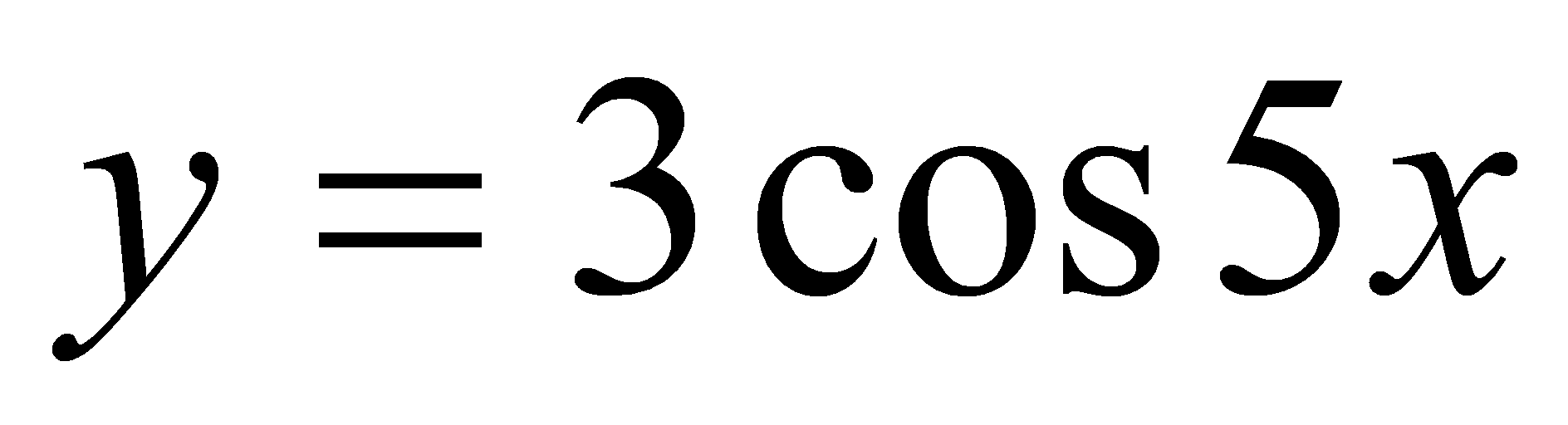 и
и
 в
точках с абсциссой
в
точках с абсциссой
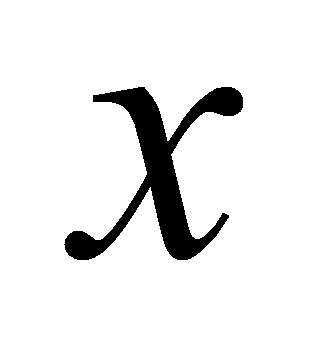 параллельны.
параллельны.
Решение.
Известно, что тангенс угла наклона касательной к графику функций
![]() в точке с абсциссой
в точке с абсциссой
![]() равен
равен
![]() .
Следовательно, все искомые значения
.
Следовательно, все искомые значения
![]() будут корнями уравнения
будут корнями уравнения
![]() ,
откуда
,
откуда
![]() .
Используя формулу разности синусов углов, будем иметь
.
Используя формулу разности синусов углов, будем иметь
![]() .
Решая полученное уравнение, получаем
.
Решая полученное уравнение, получаем
![]()
![]()
Решение. Найдем критические точки заданной функции:
Так как,
производная в точках
![]() и
и
![]() равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
![]() .
Найдем значения функций в этих точках.
.
Найдем значения функций в этих точках.
Итак,
расстояние d
между касательными, параллельными оси
![]() ,
равно
,
равно
![]()
С составлением
уравнения касательной, параллельной данной прямой, связана задача о
нахождении кратчайшего расстояния между графиком
некоторой функции f(x)
и прямой
![]() .
.
Во многих
случаях удается найти касательную к графику
![]() ,
параллельную данной прямой
,
параллельную данной прямой
![]() и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
![]() является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле

Решение.
Убедившись, что графики не имеют общих
точек (уравнение
![]() не имеет решений), запишем
уравнение такой касательной к графику функции
не имеет решений), запишем
уравнение такой касательной к графику функции
![]() ,
которая параллельна прямой
,
которая параллельна прямой
![]() Уравнение касательной имеет
вид
Уравнение касательной имеет
вид
![]() касание происходит в точке
касание происходит в точке
![]() Прямая у =
Прямая у =
![]() х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
![]() .
.
Довольно сложной является задача составления уравнения всех касательных к графику функции у = f(x), проходящих через заданную точку М(х0; у0), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:
![]()
![]()
2. Решаем
относительно t
уравнение
![]() и для каждого его
решения t
записываем
соответствующую
касательную в виде
и для каждого его
решения t
записываем
соответствующую
касательную в виде
![]() .
.
Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
![]() .
Так как эта
касательная проходит через точку
(2; -2), то
.
Так как эта
касательная проходит через точку
(2; -2), то ![]() ,
откуда
,
откуда
![]() .
.
Найти площадь треугольника, образованного касательными, проведенными к графику функции
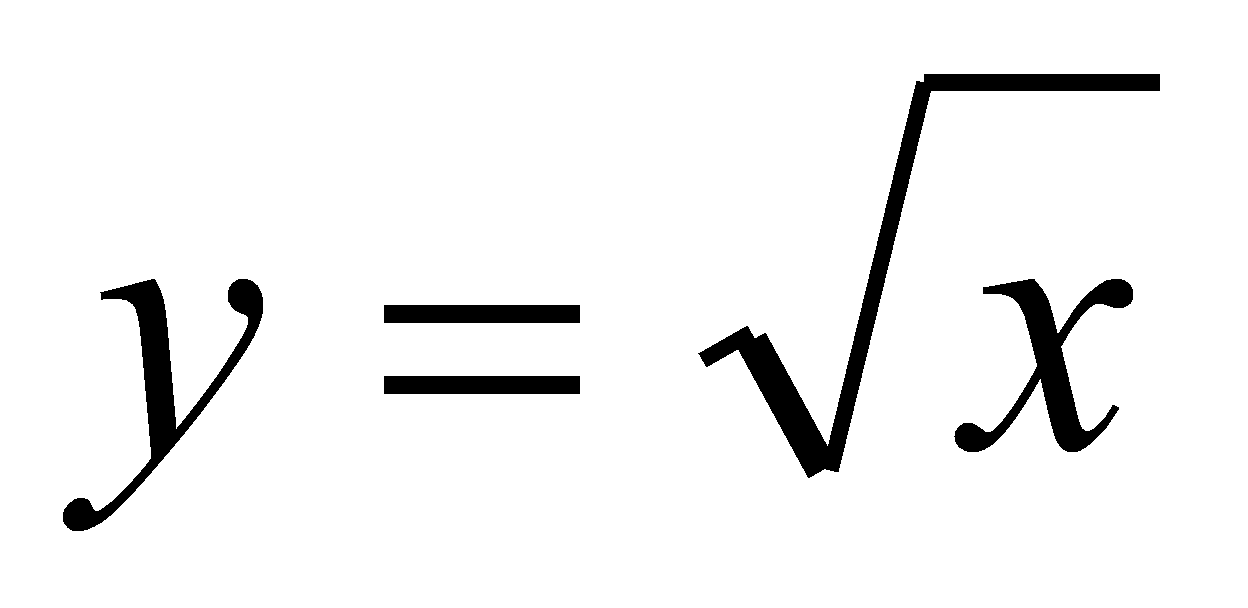 через точку
через точку
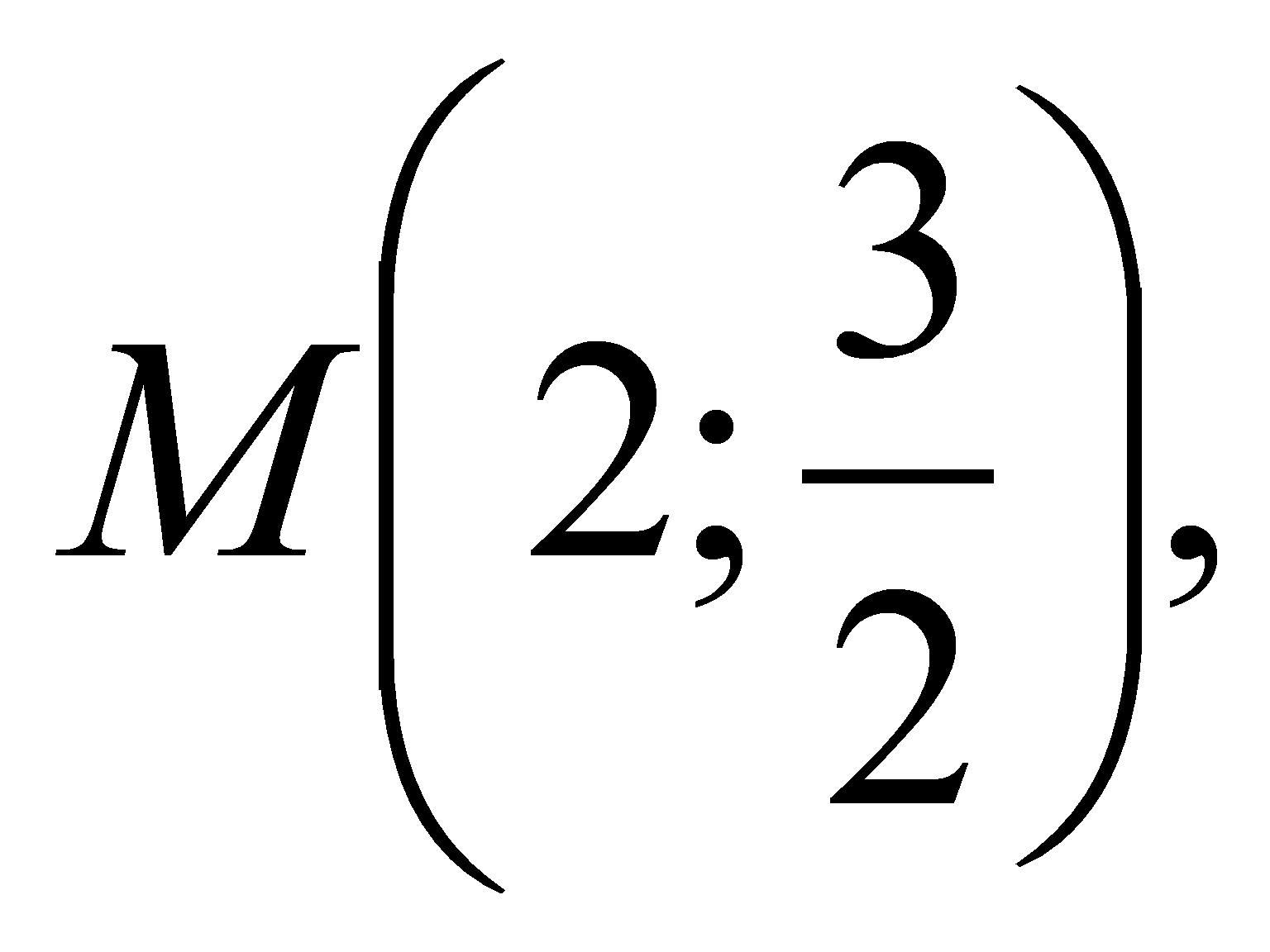 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания.
Указание.
Уравнение
![]() дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
Ответ: 0,25.
Говорят, что
прямая
![]() является общей касательной графиков функции
является общей касательной графиков функции
![]() и
и
![]() ,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
![]() является общей касательной графиков функций
является общей касательной графиков функций
![]() (в точке М(2; 5) и
(в точке М(2; 5) и
![]() (в точке K(0,5;
-1)). Заметим, что графики функций
(в точке K(0,5;
-1)). Заметим, что графики функций
![]() и
и
![]() имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
![]() .
.
Доказать, что параболы
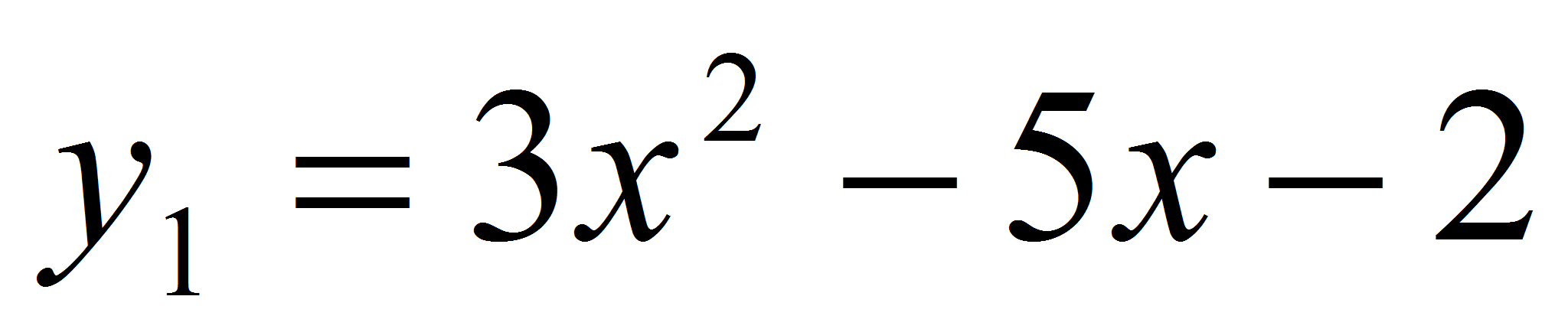 и
и
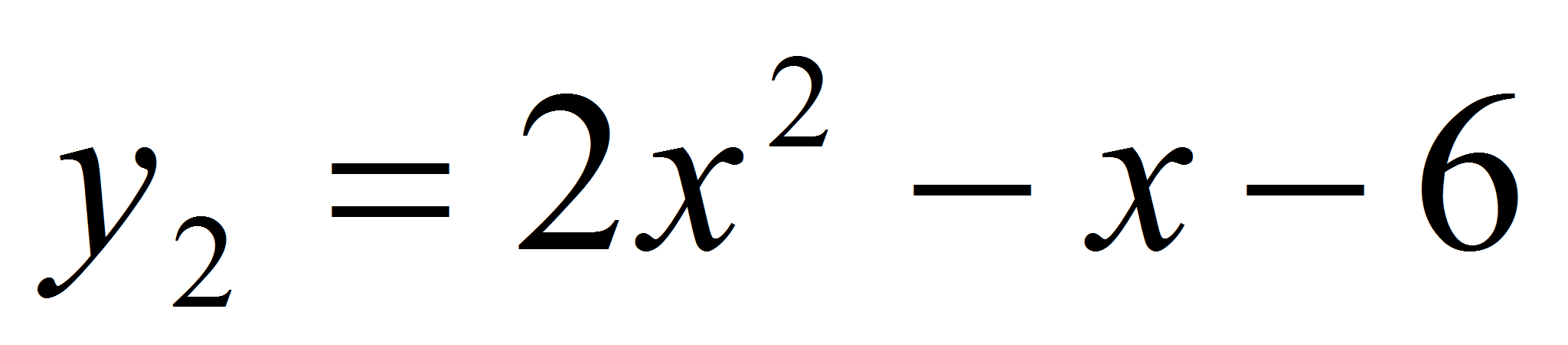 имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
 имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
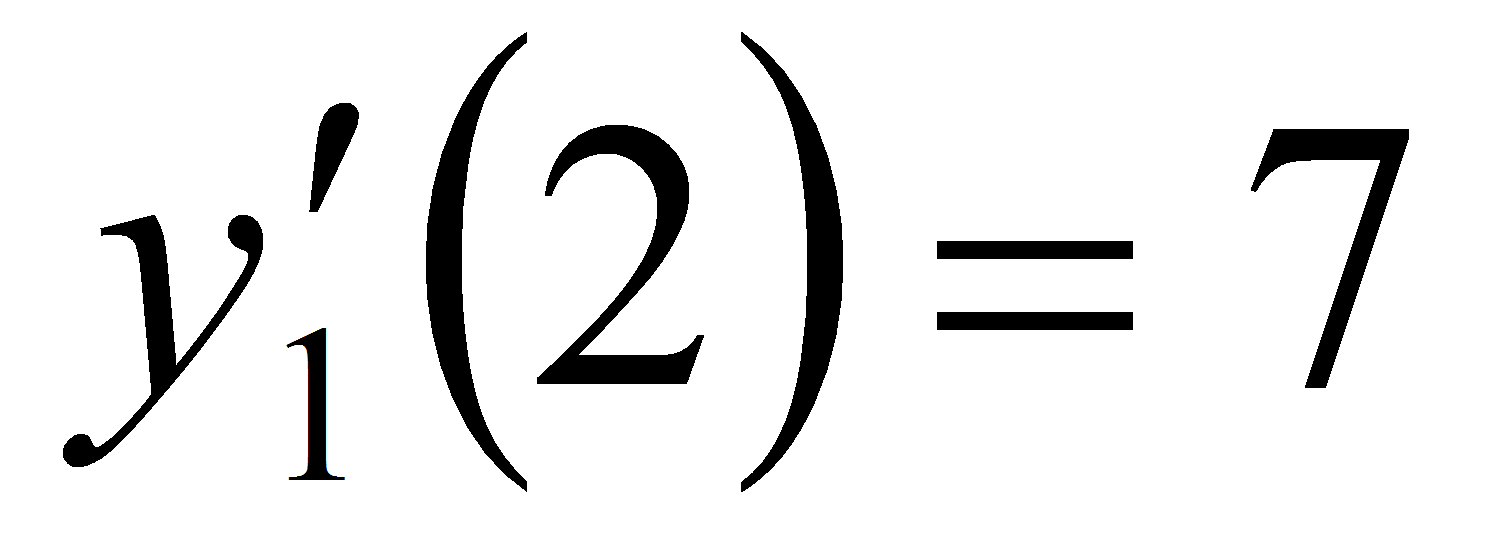 и
и
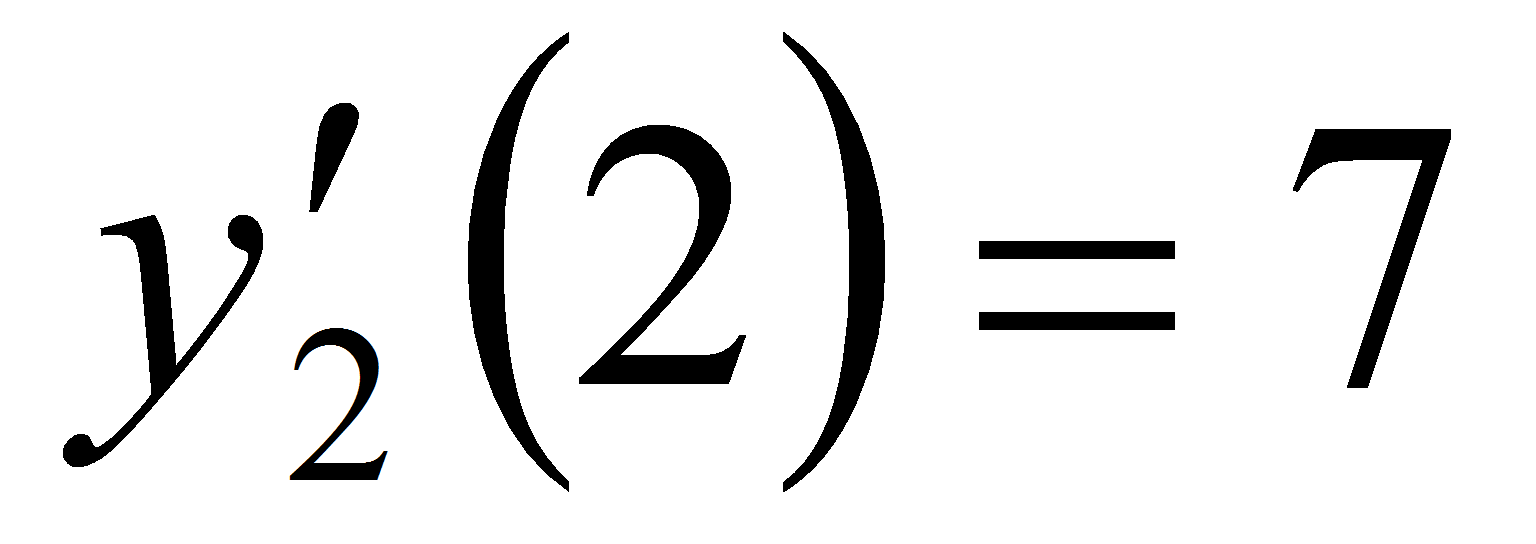 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной.
В завершении рассмотрим решение еще нескольких задач на касательную с параметром.
Решение.
Составим уравнение касательной к графику заданной функции в точке
![]() :
:
![]() Так как эта прямая проходит через точку (2;3), то имеет место
равенство
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
![]() ,
откуда находим:
,
откуда находим:
![]() .
.
Может ли касательная к кривой
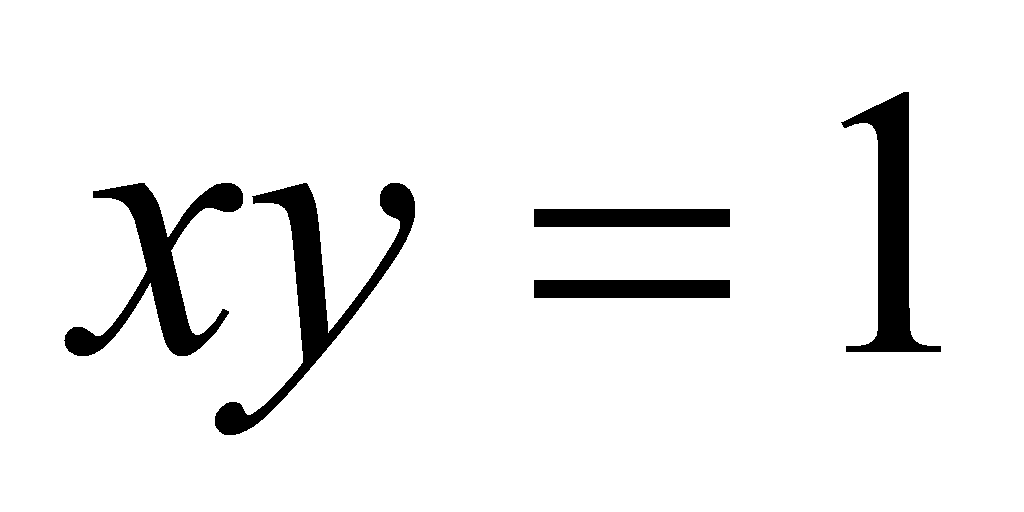 в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
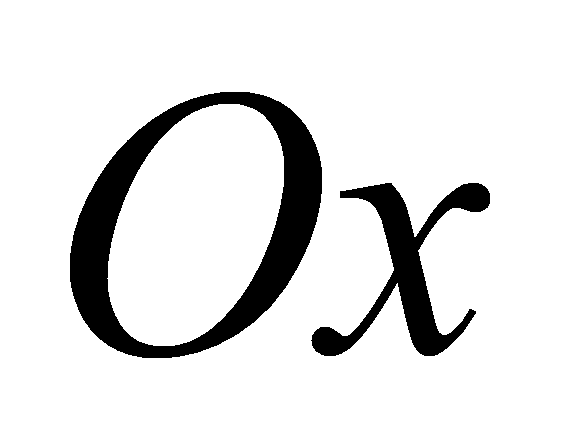 ?
?
Решение.
Найдем производную функции
![]() .
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не может.
Найти значение параметра
 ,
при котором касательная к графику функции
,
при котором касательная к графику функции
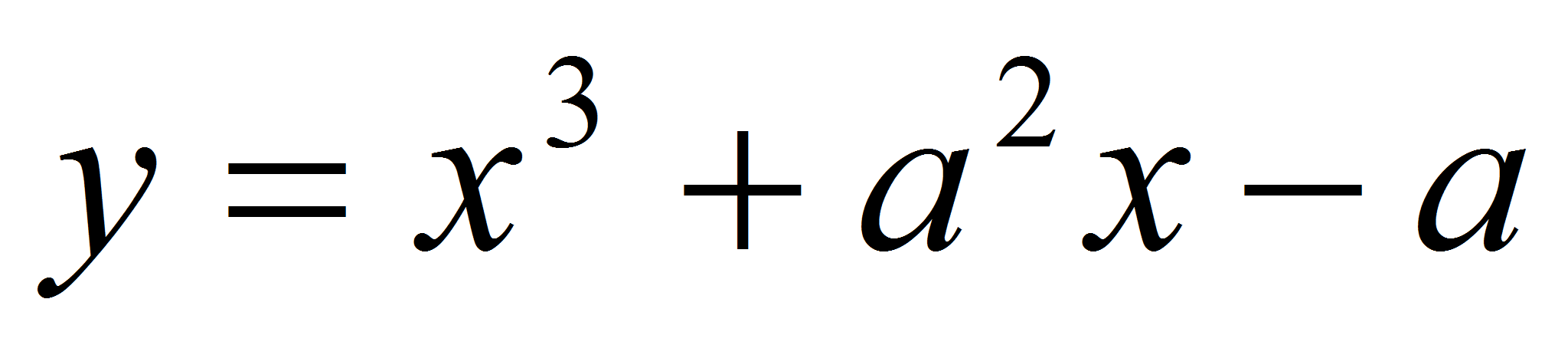 в точке
в точке
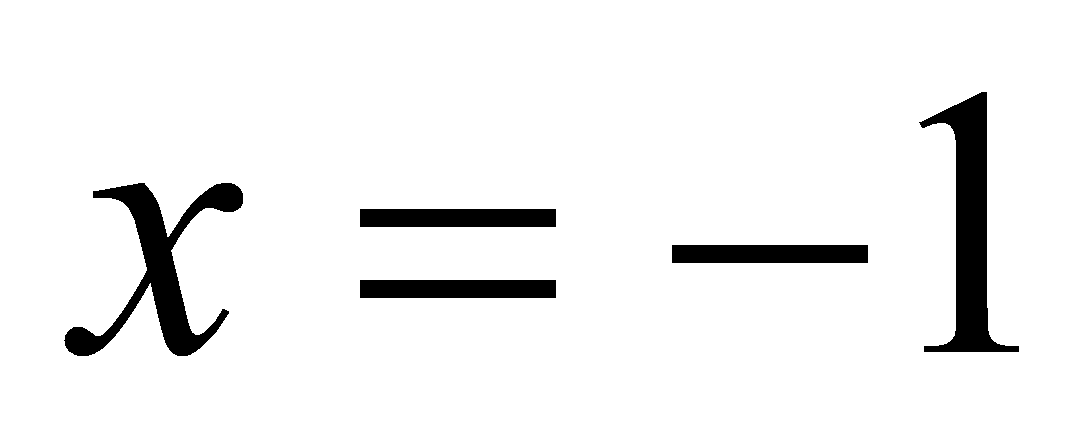 проходит через точку М(1;7).
проходит через точку М(1;7).
Решение.
Пусть
![]() тогда
тогда
![]() .
Составим уравнение касательной:
.
Составим уравнение касательной:
По условию эта
касательная проходит через точку М(1;7), значит,
![]() ,
откуда получаем:
,
откуда получаем:
![]()
Решение.
Из условия следует, что должно выполнятся равенство
![]() где
где
![]()
![]() абсцисса
точки касания. Значит,
абсцисса
точки касания. Значит,
![]() и
и
![]() связаны между собой равенством
связаны между собой равенством
![]() (1). Составим уравнение касательной к графику заданной функции в
точке
(1). Составим уравнение касательной к графику заданной функции в
точке
![]()
Из условия
следует, что должно выполняться равенство
![]() .
Решив это уравнение, получим
.
Решив это уравнение, получим
![]() .
Тогда из (1) получаем, что
.
Тогда из (1) получаем, что
![]() .
.
Решение.
Так как прямая
![]() является касательной к графику функции
является касательной к графику функции
![]() ,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() -
абсцисса точки касания. Найдем теперь
-
абсцисса точки касания. Найдем теперь
![]() из
условия равенства значений функций
из
условия равенства значений функций
![]() и
и
![]() при
при
![]() .
Имеем
.
Имеем
![]() ,
откуда
,
откуда
![]() .
.
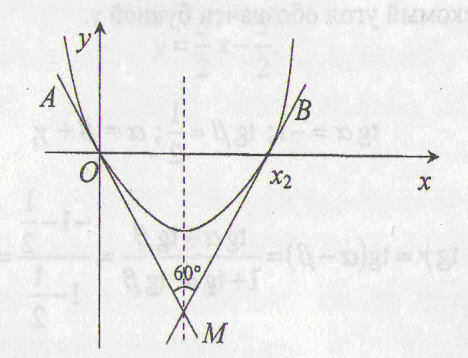
При каких значениях параметра а касательные к графику функции
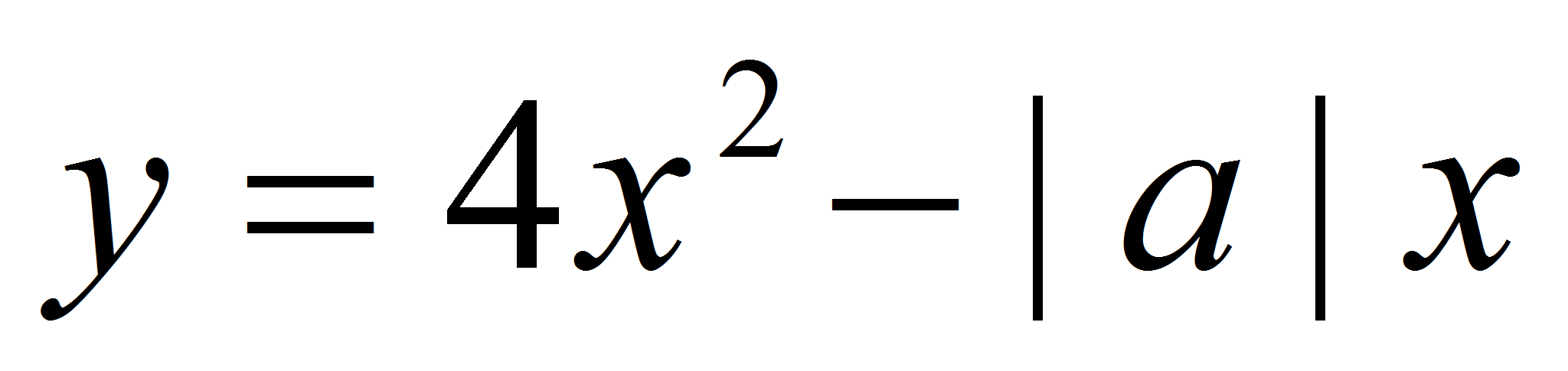 ,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
![]() и
и
![]() учитываем,
что х2>0
(рис. 3)
учитываем,
что х2>0
(рис. 3)
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
![]() ,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
![]() Далее имеем:
Далее имеем:
![]() .
Таким образом, получаем, что
.
Таким образом, получаем, что
![]() ,
то
,
то
![]() .
Во втором случае
.
Во втором случае
![]() ,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
![]() .
Таким образом, получаем, что
.
Таким образом, получаем, что
![]() ,
то есть
,
то есть
![]()
Литература:
Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.
Звавич, Л.И. Алгебра и начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.– М.: Дрофа, 1999. – 352 с.