В статье анализируются основные вопросы, связанные с формированием основ экономической и финансовой грамотности российского общества в целом, а также формированием экономических практико-ориентированных компетенций у обучающихся российских школ в частности на примере решения задач с экономическим содержанием. Рассматриваются сущность, типы и основные особенности экономических задач в структуре единого государственного экзамена по математике (профильный уровень), а также предлагаются варианты решения данных задач и методическая база.
Ключевые слова: единый государственный экзамен, экономическая задача, экономическая грамотность, финансовая грамотность.
The article analyzes the main issues related to the formation of the foundations of economic and financial knowledge of Russian society as a whole, as well as the formation of economic practice-oriented competencies of Russian schools` students, in particular, using the example of solving math tasks with economic content. The essence, types and main features of economic tasks in the structure of the unified state examination in mathematics (advanced level) are considered, as well as options for solving these tasks and a methodological base are proposed.
Keywords: unified state examination, economic task, economic knowledge, financial knowledge.
Реалии современной экономической ситуации в России, обусловленные рядом политических, социальных, технологических, правовых и международных факторов, актуализируют важность и необходимость обеспечения высокого уровня экономической и финансовой грамотности российского населения. Современной России нужны люди, способные находиться в постоянном поиске путей решения экономических проблем и эффективно осуществлять экономическую деятельность. Важное значение в системе подготовки экономически грамотного населения отводится школе, так как современная социальная среда не в состоянии обеспечить детям и подросткам практико-ориентированную подготовку к решению экономических задач их повседневной жизни.
В последнее десятилетие проблеме формирования экономического практико-ориентированного мышления подрастающего поколения уделяется в системе образования значительно больше внимания, чем в предыдущие годы: организуются и проводятся курсы по формированию финансовой грамотности населения как для педагогов, так и для детей и взрослых, издается и переиздается большое количество теоретической и практической экономической литературы, разрабатываются и реализуются образовательные проекты по развитию финансовой и экономической грамотности, предпринимательству на всех уровнях системы образования. В качестве частного случая решения выше указанных задач можно выделить включение в структуру единого государственного экзамена по математике (профильный уровень) практико-ориентированной задачи с экономическим содержанием. Данная задача в структуре контрольно-измерительных материалов экзамена (КИМ ЕГЭ) предлагается участникам экзамена во второй части (задания с развернутым ответом), имеет порядковый номер задания 15 и обладает повышенным уровнем сложности, предполагаемое время решения указанной задачи участниками экзамена составляет 25–30 минут. В спецификации КИМ ЕГЭ 2022г. и кодификаторе элементов содержания КИМ по математике можно увидеть, что задача направлена на проверку умения использовать приобретенные математические знания в практической деятельности и повседневной жизни [1,2]. У обучающихся при этом проверяется умение выполнять действия с целыми и рациональными числами, с дробями, со степенями с натуральным показателем, знаний и умений обращаться с процентами, в том числе и сложными «банковскими» процентами [3].
Однако, как показывает практика проведения единого государственного профильного экзамена по математике, у выпускников школ отмечаются существенные сложности в решении задач данного типа. Сложности в решении задачи № 15 выпускниками напрямую связаны с подготовкой к экзамену в школе. В контексте проблем в подготовке к успешному решению конкретной задачи можно выделить следующие: наличие в таких задачах большого количества терминов, неизвестных учащимся; старшеклассники плохо ориентируются в материале, изученном в 5–9 классах и необходимом для решения подобных задач (темы процентов, арифметической, геометрической прогрессий вызывают затруднения); предлагаемые для решения задачи являются сразу сложными.
Таким образом, задача методической подготовки к решению задач с экономическим содержанием, в первую очередь, педагогов подтверждает свою значимость и актуальность.
Авторами настоящей статьи рекомендовано, в первую очередь, разобраться и различать несколько типов указанной задачи, а затем, для каждого типа задачи разработать и предложить обучающимся единый алгоритм решения.
Существует 5 типов задачи № 15 с экономическим содержанием:
— Задача на кредиты;
— Задача на вклады;
— Задача на нахождение экстремумов;
— Производственно-бытовая задача;
— Задача на проценты, доли и соотношения.
Базовые формулы для решения указанных типов задач следующие:
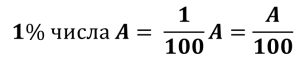
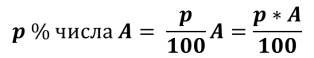
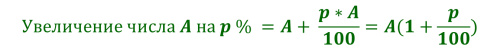
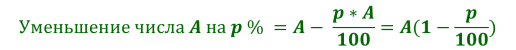
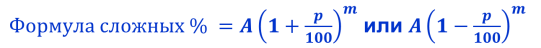
Решение задачи с экономическим содержанием, как и любой текстовой задачи происходит по следующей схеме:
- Условие задачи необходимо «перевести» на математический язык (составление математической модели).
- Найти решение задачи, используя знание математических формул (работа с составленной моделью).
- Объяснить полученный для математической модели результат в терминах первоначальной задачи.
1 тип: задача на кредиты
Пример :
31 декабря 2017 года Виталий взял в Банке 4 550 000 рублей в кредит под 20 % годовых. Схема выплаты следующая: 31 числа каждого следующего месяца Банк начисляет процент (%) на оставшуюся сумму долга (т. е. повышает долг на 20 %), затем Виталий переводит в Банк определенную сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа (в рублях), если Виталий выплатит долг тремя равными ежегодными платежами.
Решение задачи :
Обозначим сумму ежегодного платежа за Х, тогда
1 год: 4 550 000 * 1,2 — сумма к возврату после 1 года (с начисленными %)
После выплаты ежегодного платежа: 4 550 000 * 1,2 — Х
2 год: (4 550 000 * 1,2 — Х) * 1,2 — Х
3 год: ((4 550 000 * 1,2 — Х) * 1,2 — Х)* 1,2 — Х
Так как по условию задачи Виталий к концу 3 года выплатит все полностью, по состоянию на конец 3го года долг Виталия перед банком будет равен 0 рублей.
Составим уравнение (математическая модель):
((4 550 000 * 1,2 — Х) * 1,2 — Х)* 1,2 — Х = 0
Далее — математическое решение уравнения с одним неизвестным элементом.
Ответ: 2 160 000 рублей.
2 тип: задачи на вклады
Пример :
Вкладчик внес в Банк 2 500 000 рублей в год под 10 % годовых. В конце каждого из трех лет вкладчик дополнительно вносил одну и ту же сумму денег. К концу 4-го года его вклад стал равен 4 024 350 рублей. Какую сумму вносил вкладчик в течение 1–3 лет?
Данный тип задач похож на 1 тип, только сумма на счету не уменьшается, а увеличивается.
Решение :
Обозначим сумму ежегодного платежа, которую вносил на свой счет вкладчик, за Х, тогда
1 год: 2 500 000 * 1,1 — сумма к концу 1 года (с начисленными % по вкладу)
После внесения суммы на счет вкладчиком: 2 500 000 * 1,1 + Х
2 год: (2 500 000 * 1,1 + Х) * 1,1 + Х
3 год: ((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х
4 год: (((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х) * 1,1
В конце 4-го года начислены только %, так как вкладчик сумму добавлял только 1–3 года.
Составим уравнение (математическая модель):
(((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х) * 1,1 = 4 024 350
Далее — математическое решение задачи
Ответ: 100 000 рублей
3 тип: задачи на исследование функции и нахождение экстремумов
Пример :
Первичная информация некоторой фирмы распределяется по Серверам 1 и 2. С Сервера 1 при объеме W2 Гбайт входящей информации выходит 3W Гбайт, а с Сервера 2 при объеме W2 Гбайт выходит 4W Гбайт. Определите наибольший общий объем Выходящей информации, если общий объем входящей информации 400 Гбайт. В ответе укажите число Гбайт.
Когда речь в Задаче идет о предельных величинах (максимальных или минимальных значениях), — значит, эта задача связана с нахождением производной функции.
Решение :
Пусть на Сервер 1 входит Х входящей информации, а на Сервер 2 — У входящей информации, тогда
На оба Сервера будет входить Х+У = 400 Гбайт
Сервер 1: входит Х информации, выходит
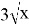
Сервер 2: входит У информации, выходит
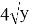
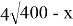
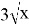
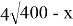
Необходимо найти точку экстремума функции
Далее — математическое решение задачи.
Х = 144 — т. е. в этом значении функции достигает максимального значения.
Найдём значение функции в указанной точке:
F (144) =
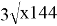
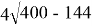
F (144) = 3*12+4*16 = 36+64=100
Ответ: 100 Гбайт.
4 тип: производственно-бытовые задачи
Пример :
Общая численность персонала завода составляет более 200 человек. Пятая часть сотрудников работает в заводоуправлении, 33 сотрудника работают в сборочном цехе, а остальные — в нескольких цехах, численность в каждом из которых составляет 1/9 от всего персонала завода. Чему равна общая численность персонала завода?
В задачах такого типа важно проявить предположение, подбор чисел, элементы эрудиции, — здесь важно предположить, каким может быть ответ, ограничить область принадлежности чисел потенциального ответа и методом подбора вариантов найти верное решение. Подбор решений основывается на знаниях кратности чисел и логике.
Решение :
Пусть общая численность персонала равна Х, тогда
X= 1/5 Х + 33+ 1/9 Х * К (К –количество цехов)
X= 1/5 Х + 33+ Х/9 * К
Х-1/5 Х — КХ/9 = 33
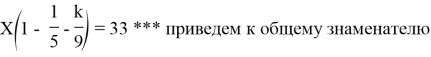
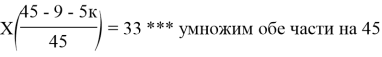
X (36–5K) = 33*45 *** теперь делаем предположение, каким может быть К
С одной стороны: 36–5К> 0, следовательно K≤7
С другой стороны: 33*45 = 1485 — нечетное, значит К — нечетное,
Таким образом возможные варианты К = 1,3,5,7
Проверяем все варианты:
К=7 — единственное решение задачи, в таком случае Х = 1485 человек
Ответ: 1485 человек.
5 тип: задачи на проценты, доли и соотношения
Пример :
Меховая шуба стоит дороже кожаной куртки на 45 %. На сколько % дешевле стоит кожаная куртка, чем меховая шуба?
В задачах такого типа важно правильно определить, что именно брать за основу, т. е. за элемент относительного сравнения (за 100 %).
Решение :
Пусть кожаная куртка стоит Х, тогда, по условию задачи меховая шуба стоит 1,45 Х
Теперь, за основу, за базу, за 100 % возьмем меховую шубу, тогда
1,45 Х — 100 %
Х — р %
Р % = 100Х / 1,45 Х = 10 000 / 145 = 68,9 % = 69 %
Кожаная куртка составляет по стоимости в НОВОМ сравнении 69 % от меховой шубы, т. е. дешевле нее на 100 % — 69 % = 31 %
Ответ: 31 %
Вышеприведенные примеры типов задач являются авторской классификацией и могут не ограничиваться только указанными примерами. КИМ ЕГЭ пересматриваются ежегодно, дополняются и совершенствуются. Указанные типы задач предложены авторами статьи в качестве методического ориентира, базовых характеристик возможных типов содержания задачи № 15 и вариантов решения. Важно дополнительно отметить, что несмотря на свою значимость, задачи, имеющие экономическое содержание, вызывают значительные трудности у обучающихся, обусловленные отсутствием достаточного внимания к решению подобных задач в школьном курсе математики, слишком большим объёмом информации, из которой трудно выделить необходимую при самостоятельной подготовке к экзамену, отсутствием общей математической культуры и экономической грамотности.
Кроме краткосрочной цели успешного прохождения экзаменационных испытаний по окончанию школы, обучение школьников решению задач с экономическим содержанием на уроках математики важно для всех категорий обучающихся благодаря из практико-ориентированному содержанию. Использование прикладных задач с экономическим содержанием позволит сформировать у выпускников школы некоторые представления об экономике страны и её месте в мировой экономике, даст возможность изучить экономические термины, встречаемые в задачах и в жизни, лучше их понять. В настоящее время, когда возрастают требования государства и общества к воспитанию конкурентоспособной личности, умеющей адаптироваться к меняющимся условиям жизнедеятельности, социально активной и компетентной в трудовой сфере, а слова «кредит», «кредитная карта», «ипотека», «вклад», «банковские проценты» не понаслышке знакомы большинству российских семей, использование задач с экономическим содержанием на уроках математики позволит продемонстрировать учащимся практическую значимость математики и одновременно подготовить их к финансовым задачам, диктуемым жизнью, т. е. быть финансово грамотным.
В Концепции программы повышения уровня финансовой грамотности населения РФ это понятие трактуют как способность граждан [4]:
— эффективно управлять личными финансами;
— осуществлять учет расходов и доходов домохозяйства и осуществлять краткосрочное и долгосрочное финансовое планирование;
— оптимизировать соотношение между сбережениями и потреблением;
— разбираться в особенностях различных финансовых продуктов и услуг (в том числе инструментов рынка ценных бумаг и коллективных инвестиций), иметь актуальную информацию о ситуации на финансовых рынках;
— принимать обоснованные решения в отношении финансовых продуктов и услуг и осознано нести ответственность за такие решения;
— компетентно планировать и осуществлять пенсионные накопления.
Изложенные обстоятельства определяют актуальность вопросов, связанных с повышением экономической грамотности школьников, и делают проблему усиления прикладной направленности математики одним из важнейших направлений развития школьного математического образования. Задачей современной школы является подготовка учащихся к успешной социальной и профессиональной адаптации в условиях рыночной экономики, и экономическая грамотность становится одним из основных критериев развития конкурентоспособной личности, приспособленной к самостоятельной жизни [5].
Литература:
- Спецификация контрольно-измерительных материалов единого государственного экзамена 2022 г. по математике [Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
- Кодификатор требований к уровню подготовки выпускников по математике для составления контрольных измерительных материалов единого государственного экзамена 2022 г. Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
- Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена по математике 2022 г. [Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
- Стратегия повышения финансовой грамотности в Российской Федерации на 2017‒2023 гг. утверждена распоряжением Правительства Российской Федерации от 25 сентября 2017 г. № 2039-р.
- Чумаченко В. В., Горяев А. П. Основы финансовой грамотности: учебное пособие для общеобразовательных организаций. — М.: Просвещение, 2019.







