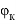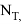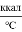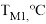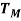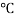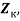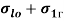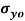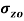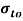В статье рассмотрены модели и аналитические зависимости для оценки тепломеханических напряжений на поверхности катания колесных пар подвижного состава. Получены формулы для составляющих температурных напряжений на поверхности катания колесной пары. Определены максимальные температуры в конце первого цикла торможения.
Ключевые слова: колесо, рельс, износ, скорость, поверхность катания, упрочнение.
Локомотивы типа ТЭ10М и ВЛ - 80,эксплуатируемые в зимний период времени на магистральных участках железных дорог Узбекистана, показывают, что на поверхностях гребней бандажей у части колесных пар возникают мелкие трещины, развитие которых приводит к их разрушениям. Проведем обобщенный анализ материалов расчетных исследований, максимальных накопленных напряжений на поверхности катания бандажа колесной пары тепловозов типа ТЭ10М. Это обусловлено явлениями периодического торможения локомотивов.
Моделирование температурных полей и напряжений в материале бандажей при торможении локомотивов проведем с использованием следующих допущений:
Оценку максимальной мощности
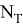
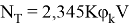
где
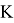
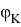
Расчетное время одного цикла торможения локомотива с поездом принимаем t T =40 с, учитывающее среднюю длину тормозного пути 800 м при средней скорости торможения 72 км/ч (20м/с).
Функцию распределения температуры в поверхностных слоях материала бандажей принимаем в виде
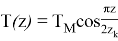
где
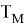
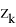
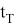
Условие теплового баланса -поглощения тепловой энергии
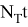
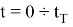
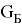
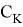
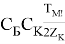
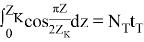
из полученного уравнения определим максимальную температуру в конце первого цикла торможения
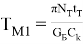
Полученные результаты расчетов
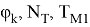
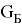
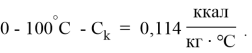
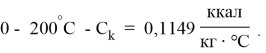
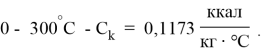
При условиях торможения тепловозов с поездами на участках с уклонами большой длины, выполняется несколько последовательных циклов торможения, на основании обобщения материалов расчетно-экспериментальных исследований рекомендуется формула для расчета максимальной накопленной температуры нагревания поверхностного слоя бандажа колесной пары локомотива
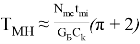
где
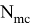
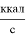
Таблица 1
Расчетные значения коэффициентов трения
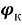
|
V км / ч |
Параметры нагревания бандажа |
Усилие К нажатия на тормозную колодку. Т |
|||
|
8,5 |
7,5 |
6,5 |
5,5 |
||
|
100 |
|
0,0726 |
0.0747 |
0,0776 |
0,0812 |
|
|
50,84 |
52,31 |
54,3 |
56,87 |
|
|
|
219,7 |
226 |
234,6 |
245,7 |
|
|
90 |
|
0,0712 |
0,0733 |
0,0762 |
0,0797 |
|
|
44,87 |
46,2 |
48,02 |
50,23 |
|
|
|
193,9 |
199,6 |
207,5 |
217,1 |
|
|
72 |
|
0,0814 |
0,0838 |
0,0871 |
0,091 |
|
|
41,04 |
42,25 |
43,92 |
45,88 |
|
|
|
177,4 |
182,6 |
189,8 |
198,3 |
|
|
54 |
|
0,0906 |
0,0932 |
0,0969 |
0,101 |
|
|
34,26 |
35,24 |
36,64 |
38,19 |
|
|
|
148,1 |
152,3 |
158,4 |
165,1 |
|
|
36 |
|
0,106 |
0,109 |
0,113 |
0,118 |
|
|
26,72 |
27,48 |
28,49 |
29,75 |
|
|
|
116,4 |
119,7 |
124,1 |
129,6 |
|
Данные экспериментальных измерений максимальных температур поверхностного слоя бандажей локомотивов согласуются с приведенными значениями Т
м1
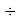
В качестве модели для возникновения температурных напряжений в материале бандажей локомотивов использовали толстостенный цилиндр, материал которого находится под воздействием стационарного теплового поля с функцией температуры по (2). Для этой модели применяли исходные аналитические зависимости методов расчета таких цилиндров по [1,с. 404–407] и следующие допущения.
Используем относительные (упругие) температурные деформации по направлениям z (по радиусу R, наружной поверхности бандажа)
-
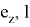
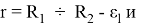
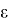
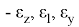
Влиянием удельных давлений Р 2 на поверхности радиусов R 2 и Р 1 , R 1 на температурные напряжения пренебрегаем; не учитывались внешние усилия, действующие на модель бандажа по направлению у.
Используя такие допущения, получим формулы для составляющих температурных напряжений на поверхности радиуса R 1 , модели бандажа колесной пары тепловозов типа ТЭ10М
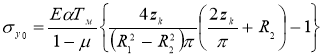
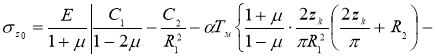
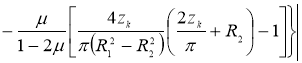
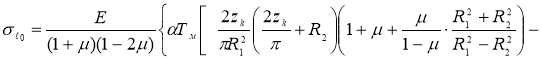
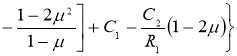
определим постоянные
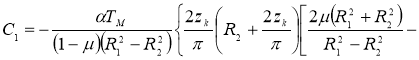
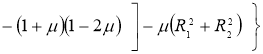
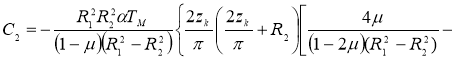
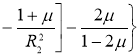
Значение коэффициента линейного расширения
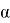
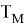
до 100°С-
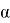
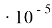
до 200°С-
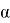
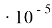
до 300°С-
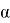
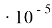
до 400°С-
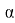
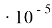
до 500°С-
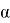
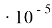
согласно обобщению данных [6,7].
Результаты расчетов
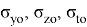
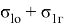
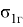
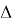
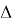
Таблица 2
Составляющие температурных напряжений в поверхностных слоях материала бандажей колесных пар тепловозов типа ТЭ10М в зависимости от температуры Т м
|
|
мм |
Составляющая температурных напряжений, МПа |
МПа |
||
|
|
|
|
|||
|
200 |
90 |
257 |
30,7 |
666 |
— |
|
75 |
259 |
24,6 |
665 |
920 |
|
|
55 |
339 |
24,0 |
687 |
950 |
|
|
35 |
444 |
47,5 |
703 |
978 |
|
|
300 |
90 |
397 |
47,3 |
1027 |
— |
|
75 |
339 |
29,7 |
1026 |
1280 |
|
|
55 |
523 |
37 |
1057 |
1320 |
|
|
35 |
685 |
73,2 |
1085 |
1360 |
|
|
400 |
90 |
945 |
65,4 |
1419 |
— |
|
75 |
551 |
38,6 |
1417 |
1671 |
|
|
55 |
723 |
51,1 |
1462 |
1725 |
|
|
35 |
945 |
101 |
1498 |
1773 |
|
|
500 |
90 |
1205 |
129 |
1807 |
— |
|
75 |
702 |
52,5 |
1804 |
2058 |
|
|
55 |
921 |
65,1 |
1863 |
2126 |
|
|
35 |
1204 |
129 |
1908 |
2183 |
|
В случае оценки максимальных напряжений по относительной температурной деформации при Т
м
=300°С и
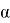
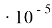
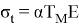
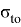
Литература:
- Писаренко Г. С., Яковлев А. П., Матвеев В. В. Справочник по сопротивлению материалов. Киев.: Наукова думка, 1975.
- Справочник по электроподвижному составу, тепловозам и дизель-поездам. Т. 1 Под ред. А. Н. Тищенко. М.: Транспорт, 1976.
- Глущенко А. Д., Файзибаев Ш.С Моделирование импульсного динамического и теплового материала колесных пар локомотивов. Ташкент.: Фан, 2002.
- Файзибаев Ш. С. Самборская Н. А. Мамаев Ш.И Моделирование импульсного динамического нагружения на криволинейных поверхностях контакта. IV- научно-практическая конференция «Актуальные вопросы и перспективы развития транспортного и строительного комплексов»Гомель 2018г.
- Файзибаев Ш. С. Набиев Э.С Температурные напряжения в материале железнодорожного колеса. Проблемы механики, 2018, № 1.
- Глущенко А. Д., Файзибаев Ш. С. Моделирование связанных автоколебаний относа,виляния и подергивания идеального экипажа локомотива в кривых участках рельсового пути //Ж. Доклады. АН РУз.2001. № 4–5.
- Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике М.: Наука, ГРФМЛ, 1974 с 255
- Файзибаев Ш. С., Соболева И. Ю., Нигай Р. П., Мамаев Ш. И., Абдирахманов Ж. А. Исследование влияния пластических деформаций на поверхности упрочняемого бандажа. Научный журнал Universum: технические науки. Москва, 2022, № 1(94)