Символы Ландау имеют широкий спектр приложений в области математического анализа, функционального анализа и математической физики. Ниже мы рассмотрим применение этих символов к задачам математического анализа.
Ключевые слова : символы Ландау, большое «О», маленькое «О», предельный знак, интегральная сумма.
Большое «О» и малое «о», известные под общим названием символы Ландау, находят применение во многих областях математики. В частности, эти символы широко используются при доказательстве ряда теорем математического анализа, получении асимптотических оценок и решении примеров. Ниже приведены основные определения и теоремы об этих символах, а также решения ряда интересных и актуальных примеров.
Определение 1
. Если функция
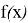
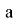
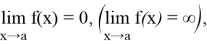
соотношение выполнено, то функция
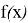
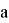
Пример 1.
Функция
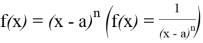
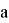
Следует отметить, что если функция
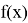
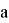
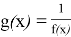
Определение 2.
Для функций
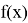
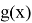

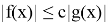
неравенство выполнено то достаточно мало вокруг точки
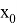
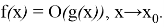
Здесь
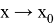
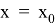
Лемма 1.
Пусть функции
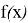
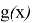
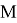
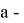
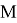
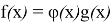
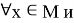
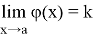
есть предел, справедливо уравнение
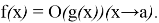
Определение 3.
Если функции
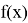
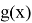
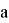
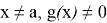
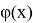
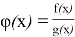
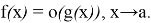
Знак
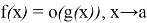
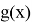
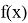
Пример 2.
Для функций
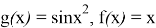
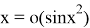
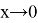
При решении следующих примеров мы используем «предельный знак сравнения» ([1], 354-ст.) , который позволяет легко проверять сходящих несобственных интегралов и рядов.
Пример 3.
При каких значениях параметра
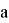
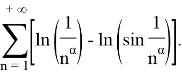
Решение: Запишем общий член ряди следующим образом:
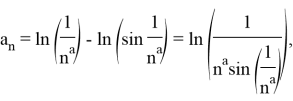
Известно, что подходит следующее распределение:
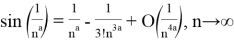
Подставляем это уравнение в приведенное выше выражение. В результате получаем:
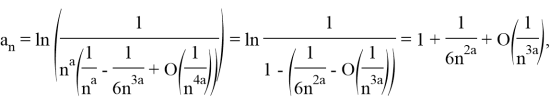
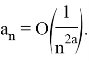
Следовательно,
«по предельному знаку сравнения»
([1]) общими членами которого являются
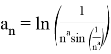
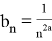
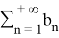
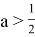
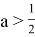
Пример 4.
Если функция
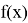
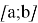
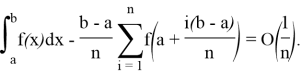
Решение.
Так как функция
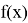
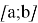
На сегменте
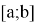
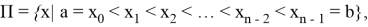
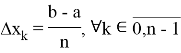
Построим нижний и верхний интегральные суммы Дарбу согласно этому делению.
Для наглядности назовем функцию
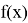
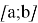
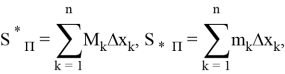
Здесь
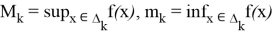
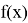
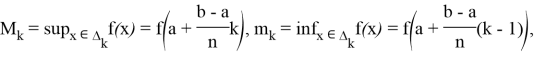
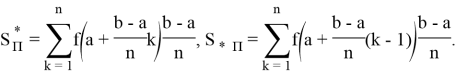
Итак, мы можем написать:
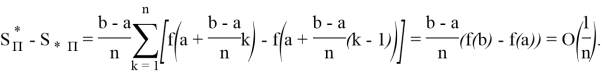
Мы знаем это,
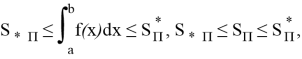
Здесь
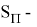
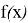
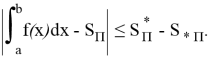
Это приводит к следующему отношению:
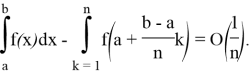
Пример 5. Проверьте сходимость несобственного интеграла:
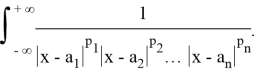
Решение.
Для функции
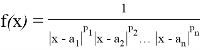
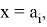
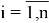
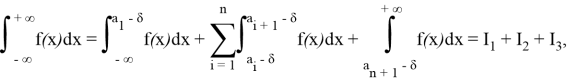
Теперь рассмотрим сходимость каждого интеграла правой части уравнения:
1)
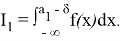
Используем «предельный знак сравнения»:
Если рассматривать функцию
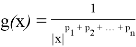
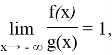
Следовательно,
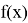
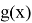
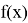
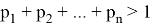
2)
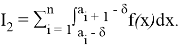
Если взять функцию
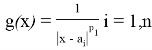
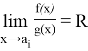
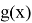
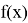
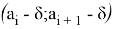
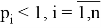
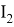
3) Непосредственно проверяется, что интеграл
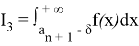
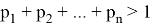
Следовательно, интеграл
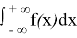
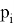
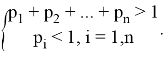
Пример 6.
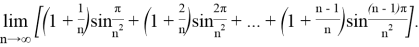
Решение. Запишем данное выражение в следующем виде:
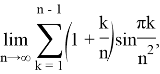
Согласно лемме 1 справедливо соотношение
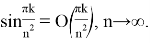
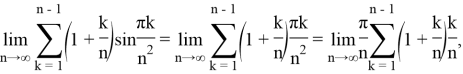
Известно, что предел этой суммы равен точному интегралу от функции
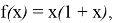
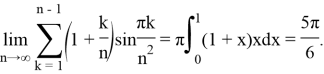
Литература:
- Alimov Sh. O. Ashurov R. R. Matematik tahlil. (1-qism). Toshkent. «Kamolot-press», 2012.
- Robert W., Heath Jr., Angel Lozano. Landau symbols. Published online by Cambridge University Press: 10 December 2018.
- Фихтенгольц Г. М. Курс дифференциального и интегральногo исчисления. — М: Наука, 1966.
- Настушка Козакова. Символы Ландау и некоторые пространство, связанные с ними. https://pandia.ru/text/78/099/121981.php







