В математике у правил нет исключений. Это знают все. Но есть дети, которые прекрасно знают правила, но не могут их применить, или применяют бездумно. Для того чтобы они поняли, насколько точно правила отражают тот или иной факт, я готовлю им задания, в которых есть подвох (ловушка). Это может быть подборка заданий для устного решения или математический диктант или задания с развернутым ответом. Подойдет любое задание, которое заставит ученика задуматься, а затем понять и запомнить материал. На практике это выглядит следующим образом:
Пример 1. Тема «Сравнение обыкновенных дробей», 5 класс. Все учащиеся прекрасно умеют сравнивать дроби, у которых равны числители (чем меньше знаменатель, тем больше дробь) и дроби, у которых равны знаменатели (чем больше знаменатель, тем больше дробь). И отрабатывая эти два правила, мы мало уделяем внимания правилу сравнения правильной и неправильной дробей. В учебнике Никольского С. М. «Математика, 5» их действительно немного. Пример устного задания ученикам: «Сравнить дроби: а)

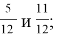
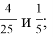


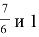
Пример 2. Тема «Треугольники», 5 класс. Наглядно показываем, что треугольник со сторонами 5 см, 4 см и 3 см построить можно, а со сторонами 15 см, 3 см и 7 см построить нельзя. Делаем вывод, что сумма двух сторон должна быть больше третьей стороны. Ловушка заключена в задании «Найти периметр треугольника со сторонами 7 см, 12 см и 3 см», так как такого треугольника не существует.
Пример 3. Тема «Треугольники», 5 класс.
Учащиеся знакомятся с понятием равнобедренный треугольник. Предлагается две задачи: 1) «Две стороны равнобедренного треугольника равны 25 см и 18 см. Чему равна третья сторона?»; 2) «Две стороны равнобедренного треугольника равны 25 см и 8 см. Чему равна третья сторона?». Подвох в том, что первая задача имеет два решения, а вторая только одно. И ученики объясняют, почему такой исход.
Пример 4. Тема «Признаки равенства треугольников», 7 класс. Пройдены все признаки равенства треугольников. Ученикам предлагается задание выбрать верные утверждения среди предложенных:
а). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам второго треугольника, то такие треугольники равны.
б). Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу второго треугольника, то такие треугольники равны.
в). Если три угла одного треугольника равны трем углам второго треугольника, то такие треугольники равны.
Ответ: а).
Разбирая детально каждое утверждение, приходим к выводу, что формулировка б) неточная, в) ошибочная.
Пример 5. Тема «Значение синуса произвольного угла», 11 класс. На вопрос «Какие значения принимает синус угла?» практически все учащиеся отвечают «Все значения из отрезка [-1;1]». Проходит минут 10–15. Учащимся задается вопрос: Есть ли угол, синус которого равен



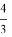
Пример 6. Тема «Определение тангенса угла», 10 класс. Задание «Найти тангенс углов

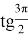
Пример 7. «Арифметический корень натуральной степени», 10 класс. Определение звучит так: «Арифметическим корнем натуральной степени
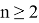
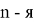
Задание 1. Вычислить

Задание 2. Упростить выражение
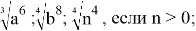
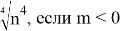

При упрощении одного и того же выражения, но при разных условиях на переменную, получены различные ответы.
Пример 8. Задание с развернутым ответом. Упростить выражение
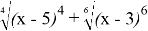
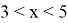
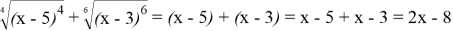
Ошибка в том, что многие ученики забывают формулу


Ловушка заключена в неверном равенстве
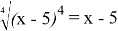
Пример 9. «Иррациональные уравнения», 10 класс. Приведу пример самой распространенной ошибки в этой теме.
Решить уравнение
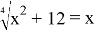
При решении этого задания учащиеся сначала делают вывод, что подкоренное выражение принимает только положительные значения. И это верно. Потом возводят обе части в 4-ю степень и решают биквадратное уравнение. В результате получают 2 и
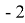
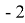
Математические диктанты по геометрии.
Пример 10. Тема «определение понятий прямая и плоскость», 10 класс.
Начертите параллелепипед ABCDA1B1C1D1
- Назовите две плоскости, в которых лежит прямая АВ.
- Проведите прямую AB 1 . Выпишите три плоскости, содержащие данную прямую.
- Закрасьте плоскость ADD 1 .
- Назовите прямую, общую для плоскостей BCC 1 и BAA 1 .
- Назовите точку, общую для плоскостей A 1 BB, A 1 D 1 D и DBC.
Пример 11. Тема «Прямоугольный параллелепипед», 10 класс.
Начертите параллелепипед ABCDEFGH
- Запишите названия 2 боковых ребер
- Запишите название граней, смежных к грани ABCD.
- Запишите название грани, противоположной к грани CDHG
- Запишите вершину, противоположную к вершине D
- Запишите все диагонали параллелепипеда
- Диагонали параллелепипеда BH и DF пересекаются в точке О. DB=6, BH=10. Найти периметр треугольника DBО.
Пример 12. Тема «Треугольник». 7 класс.
Карточки на отработку понятий «Элементы треугольника»
|
∆ QWE Стороны __________________________ Вершины __________________________ Углы _____________________________ Сторона, противолежащая вершине Q -_____, W — ____, E — ______ Угол, противолежащий стороне QW — ____, WE — ____, QE — ___. Углы, прилежащие к стороне QW — ___________ |
∆ RTY Стороны __________________________ Вершины __________________________ Углы _____________________________ Сторона, противолежащая вершине R -_____, T — ____, Y — ______ Угол, противолежащий стороне RT — ____, RY — ____, TY — ___. Углы, прилежащие к стороне RY — ___________ |
Практически каждая тема содержит что-то на первый взгляд несущественное, но оказывается, что это несущественное сильно влияет на результат. Очень важно научить ребят видеть вроде бы незаметные, но такие важные детали. И когда ученик понимает, что у него все получилось, он обошел все ловушки и решил то, что до этого было нерешаемо, учитель только улыбнется на выкрик «Ура! До меня дошло!». Это самый большой стимул в моей работе.
Конечно, на уроке используется намного больше технологий для отработки навыков, чем описано в данной статье. Применяется много дополнительного материала из различных пособий, разработок коллег, заданий с просторов интернета. На своих уроках я стараюсь учитывать способности и возможности своих учеников, чтобы им было легче воспринимать материал, и не забыть его по прошествии некоторого времени.







