Работа посвящена исследованию обратной задачи для одногопараболического уравнения, возникающего при моделировании процесса денежного моделирования. Дополнительная информация для решения обратной задачи задается в некоторой точке. Доказательство существования и единственности решения основано на сведении ее к интегральному уравнению относительно неизвестной функции .
Ключевые слова: обратные задачи, параболическое уравнение, уравнение Вольтерра.
The work is devoted to the study of the inverse problem for one parabolic equation that arose in the course of modeling the process of monetary modeling. Additional information for solving the inverse problem is given at some point. The proof of the existence and uniqueness of the solution is based on its reduction to an integral equation for an unknown function.
Keywords : inverse problems, parabolic equation, Volterra equation.
В последние годы возрос интерес к решению задач в частных производных, возникающих в финансовой математике и в экономике, в частности, процесс о денежном накоплении. Подход математического моделирования к этой проблеме приводит к изучению уравнений параболического типа. Модели предложенные в последние годы, например в [1], является стохастическими.
Обратные задачи экономики и финансовой математики : определение параметров математических моделей экономики по наблюдаемым данным, прогноз развития экономической и финансовой ситуации и т. д.
Денежные накопления — чистый доход общества, создаваемый и реализуемый на предприятии, в домашнем хозяйстве, в бизнесе в денежной форме, в виде чистого дохода, прибыли, затрачиваемой на накопления.
Известно, что [1] для математического моделирования денежных накоплений семьи предварительно необходимо ввести некоторые упрощающие допущения, применяемые при моделировании, а также функции и параметры, В реальности накопления семьи имеют в большей степени дискретный характер: семья получает зарплату и накопления семьи скачкообразно возрастают и далее не изменяются до ближайшей траты денег. При расходах накопления семьи скачкообразно уменьшаются, то есть накопления определяются кусочно-постоянной функцией времени.
Пусть конкретная семья к моменту времени
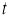
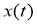
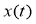
Для математического моделирования денежных накоплений семьи предварительно введем некоторые упрощающие допущения, которые применяются при моделировании, а также функции и параметры, описывающие динамику денежных накоплений. При этом применяется принцип сплошных сред , который используется при моделировании.
Постановка обратной задачи для уравнения денежных накоплений
В работе [3] дан строгий вывод уравнения денежных накоплений для так называемого ансамбля семей, которое является уравнением параболического типа
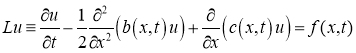
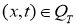
где
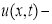
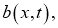
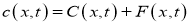
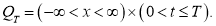
Из множества решений уравнения (1) необходимо найти единственное решение, которое адекватно описывает динамику накоплений выделенного множества семей, схожих по своей экономической деятельности. Для этого необходимо наложить некоторые дополнительные условия, возникающие в зависимости от дополнительной информации, которой обладает исследователь. Сформулируем задачу Коши для уравнения (1) по аналогии с задачей Коши для уравнения математической физики.
Задача Коши на пространстве накоплений.
Предположим, что в начальный момент времени
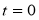
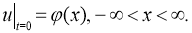
Таким образом, получили следующую задачу Коши: требуется найти решение
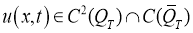
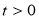
Пусть
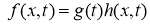
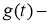
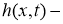
Обратная задача.
Найти пару функций
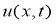
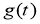
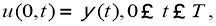
Теорема 1.
Пусть
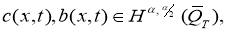
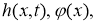
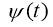
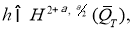
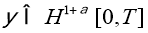
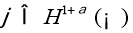
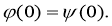
Доказательство. Заметим, что так как задача (1) — (3) линейна, то ее решение можно искать в виде
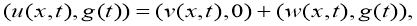
где
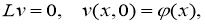
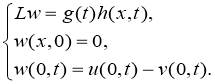
Отсюда следует, что для доказательства теоремы разрешимости задачи (1) — (3) достаточно доказать существование и единственность решения обратной задачи определения пары функций
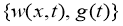
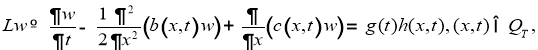
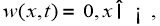
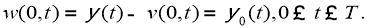
Известно [5], что решение прямой задачи (4) — (5) в пространства
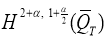
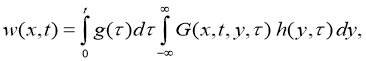
где
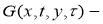
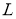
Подставляя (7) в (4), и применяя дополнительную информацию (6) для функции
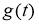
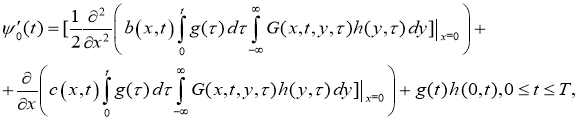
или
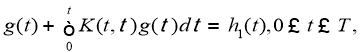
где
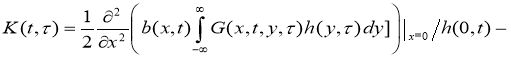
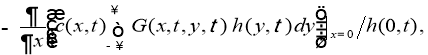
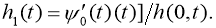
Покажем, что ядро
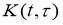
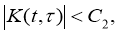
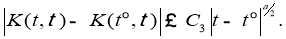
Для доказательства неравенства (9), (10) рассматривается задача Коши для функции и
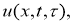
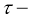
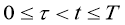
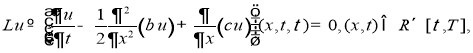
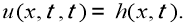
Решение задачи (11), (12) можно представить через фундаментальное решение
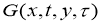
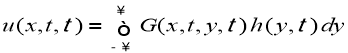
Перепишем
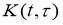
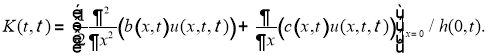
Так как коэффициенты оператора
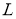
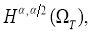
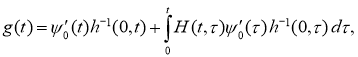
где функция
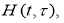
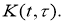
Покажем, что функция
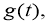
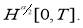
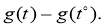
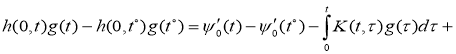
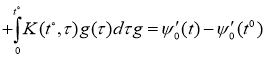
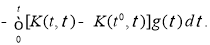
Из (9), (10), (15), (16) и предположений теоремы получаем неравенство
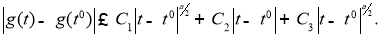
Из (17) следует, что
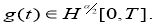
Далее, покажем, что пара функций
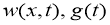
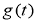
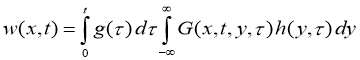
Функция
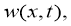
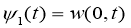
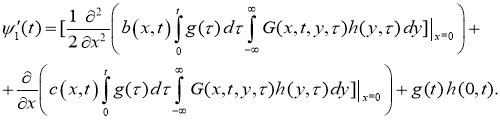
Так как
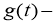
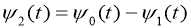
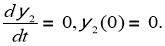
Следовательно,
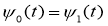
Отметим, что доказано не только существование решения, но и дан метод нахождения функции
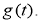
Единственность решения задачи I следует из следующей леммы.
Лемма.
Пара функций
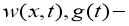
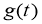
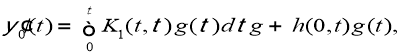
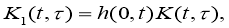
а функция
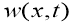
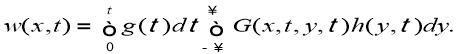
Доказательство.
Было доказано, что если
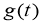
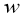
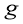
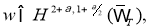
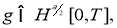
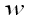
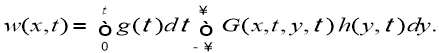
Из условия (3) и уравнения (1) получаем, что
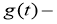
Таким образом, мы показали, что решение обратной задачи (1) — (3) существует и единственно. Теорема доказана.
Литература:
- Оксендаль Б. Стохастические дифференциальные уравнения: Введение в теорию и приложения. М.: Мир, 2003.
- Чернавский Д. С., Попков Ю. С., Рахимов А. Х. Математические модели типологии семейных накоплений // Экономика и математические методы. 1994. Т.30. Вып.2. С. 98–106.
- Ерофеенко В. Т., Козловская И. С. Уравнения с частными производными и математические модели в экономике: Курс лекций. Изд. Стереотипное. — М.: Книжный дом «ЛИБРОКОМ», 2018. — 248 с.
- Аблабеков, Б. С. Обратные задачи для дифференциальных уравнений математической физики. -учеб, пособие. –Бишкек: КГНУ, 1997. — 184 с.







