The topic «Logarithms», which is one of the leading topics in the mathematics course of secondary school, is an entrenched, but very difficult for students due to the presentation of the variety of material. «It is very important to master the method of solving logarithmic equations, as the mental and creative abilities of students increase, the first skills of research work are acquired, the mathematical culture of students is enriched, the abilities for logical thinking are developed, repetition, expansion and deeper assimilation of educational material occur» [2].
For successful mastery of the mathematical system of knowledge, in the lessons it is necessary to pay sufficient attention to the solution of logarithmic equations. Subject to the use in the classroom of certain techniques, a set of exercises and tasks that are aimed at awakening interest in mathematics when teaching this topic, students have an interest in studying it.
Another difficulty associated with the study of this topic is caused by the allocation of a small number of hours for its study on the basis of the FSES SGE, which entered into force on May 17, 2012.
The requirements FSES of the are due to three components of mastering the subject «Mathematics»:
- Ensuring the value orientation of students, knowledge of moral norms and the ability to follow them truthfulness, responsibility, education of attitude to mathematics as a part of universal human culture, which plays a special role in social development, form the personal component of the student.
- Ensuring the organization of educational activities: planning, control, goal-setting, self-regulation, defending one's point of view, the ability to make arguments, confirming them with facts, form the meta-subject component of the student.
- Application in various situations of skills mastered in the course of studying academic subjects, the formation of a scientific type of thinking, possession of mathematical terminology, methods and techniques form the subject component.
The system-activity approach is the methodological basis of the standard. It provides the design of a developing educational environment of an educational institution and the active cognitive activity of students.
Considering the existing mathematics programs, the study of logarithms and logarithmic function in secondary school is given a different place in the course of algebra and began the analysis of the 11th grade:
— in the textbook of A. G. Mordkovich the topic «Logarithms. Logarithmic equations» are studied in Chapter 7 «Exponential and logarithmic function», paragraph 41 «The concept of logarithm» and paragraph 44 «Logarithmic equations». 5 hours are allotted for the study of the topic [5].
— in the textbook of S. M. Nikolsky it is studied in chapter 1 «Roots, degrees, logarithms» paragraph 5 «Logarithms» and paragraph 6 «Exponential and logarithmic equations and inequalities» paragraph 6.2 «Simplest logarithmic equations». 2 hours are allocated for the study of the topic [6].
— In the textbook of A.Sh. Alimov, the topic is presented in chapter 4 «Logarithmic function», paragraphs 15–19 [2].
— In the textbook of N. Y. Vilenkin in chapter 8 «Indicative, logarithmic and power functions» paragraph 2 «Indicative and logarithmic equations and inequalities» paragraphs 3–4 [5].
— In the textbook of A. N. Kolmogorov, the topic is studied in chapter 4 «Indicative and logarithmic functions» paragraph 10 «Indicative and logarithmic functions» paragraphs 37–39 [1].
The study of the topic in the last three textbooks is given 6 hours.
Classification of tasks on the topic «Logarithms. Logarithmic equations» can be produced as follows:
— tasks to find the scope of definition;
— tasks for building a graph of the function;
— tasks for generalization of knowledge on several topics [3].
To solve the problems of the school course of algebra on this topic, it is enough to know the definition and properties of logarithms. For example
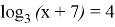
You must use the following logarithm property:
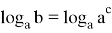
then we get:
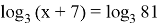
Discarding the sign of the logarithm and solving the linear equation, we find the desired answer x = 74.
When studying this topic, the main methods for solving logarithmic equations are highlighted:
— based on the definition of logarithm;
— Bringing to one ground;
— substitution method (usually this method is used to bring an equation to a square);
— potentiation method (transition from equality containing logarithms to equality that does not contain them);
— logarithm method;
— graphical method (mainly used in the case when the equation contains a variable not only under the sign of logarithm, or in the exponent).
Explaining the topic «Logarithmic equations» and revealing the methods of their solution, you can use the multimedia program «Mathematics. Solving equations and inequalities» [4]. The study of the topic of the course is based on the visual and phonemic perception of information.
The equation and its solution are reproduced on the projector screen and accompanied by a sound explanation. The most important points of the decision are highlighted in a different font from the main font.
«Algebra and the beginning of analysis. Final certification of graduates» is an educational and methodological complex designed to develop skills to solve various types of equations. Such tasks include logarithmic equations. WCU helps students to work out the skills of solving logarithmic equations. The undoubted advantage of both programs is hints and references to the theoretical part.
From a methodological point of view, it would be correct to complete each type of logarithmic equations with problems using the type of such equations. Firstly, it is difficult for students to get used to the concept of «logarithm» for a small number of classes, because this concept for eleventh-graders is new, previously unexplored; secondly, the use of such tasks improves the consolidation of the material covered; Thirdly, the solution of equations contributes to the development of mathematical and logical culture of schoolchildren.
It is best to start studying the topic with lectures. Theoretical material should clearly reflect the essence of the topic and contribute to the formation of practical skills. The lecture can be as follows:
«The simplest logarithmic equation, or an equation containing the unknown under the sign of logarithm, is log a x = b , where x is an unknown variable, a and b is some numbers».
The logarithmic function
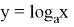
The main way to solve logarithmic equations is potentiation. This method is convenient because its result is an algebraic linear equation. When solving an equation, there is a need for verification, because there are possible options for the appearance of extraneous roots.
When solving logarithmic equations, use the properties of the logarithmic function. Here it is necessary to represent the left and right parts as logarithms with the same bases. A necessary step in the solution taking into account the scope of the definition of the logarithmic function is necessary in the solution.
Theorem: The equation
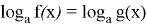
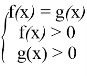
(In this system, you can omit one of the inequalities, because if one of them is greater than zero, then the other automatically becomes positive).
Therefore, to solve the equation it is necessary:
a) solve equation f (x) = g (x);
b) select from the obtained roots satisfying one of the inequalities f (x) >0, or g (x) >0, and discard the remaining roots (they are extraneous to this equation).
Based on the foregoing, it is possible to develop the following methodological recommendations in teaching the solution of logarithmic equations:
- At the initial stage of training, it is important to give meaningful, and at the same time understandable theoretical material to students. It is impossible to learn the practical foundations of the solution without knowledge of the theory.
- Teaching the solution of logarithmic equations, it is important to develop in students the ability to find ODS equations. This is necessary in order not to make a check in the future.
- The practical part of training should begin with the simplest tasks, gradually moving to more complex ones. It is important to develop a system of skills and abilities on this topic.
- The topic «Logarithmic equations» is one of the most difficult in the course of algebra of the 11th grade. Therefore, it needs to be given more attention when studying, given the fact that the works of the Unified State Exam in mathematics are based on the tasks of this topic.
Литература:
- Колмогоров А. Н. Алгебра и начала анализа: учеб. для 10–11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под ред. А. Н. Колмогорова. — 16-е изд. — М.: Просвещение, 2007. — 384с.: ил.
- Лисаченко О. А., Яковенко И. В. Особенности методики построения системы задач для изучения темы «Логарифмы. Логарифмические уравнения».Вестник Таганрогского государственного педагогического института. 2017 № 1.С. 287–292.
- Ляхова Н. Е. Использование ограниченности функций в школьном курсе математики / Н. Е. Ляхова, А. И. Гришина, И. В. Яковенко // Вестник Таганрогского государственного педагогического института. 2015. № 1. — С. 3–10.
- Математика. Решение уравнений и неравенств [Электронный ресурс]. — М., 2017. — Электрон. опт. диск (CD-Rom).
- Мордкович А. Г. Математика: алгебра и начала математического анализа, 11 класс: учебник для учащихся общеобразовательных организаций (базовый и углублённый уровни)/ А. Г. Мордкович, П. В. Семёнов. — 2-е изд., стер. — М.: Мнемозина, 2014. — 311 с.: ил.
- Никольский С. М. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин.- 8-е изд. — М.: Просвещение, 2009. — 464 с.: ил.







