Решение начальной задачи для линейных рекуррентных соотношений первого порядка в случае одношагового расщепления



Рассматривается начальная задача для неоднородного линейного рекуррентного соотношения первого порядка с операторными коэффициентами , задаваемыми квадратными числовыми матрицами. Оператор необратим, вследствие чего задача имеет решение не при каждом значении начального элемента. Применяется метод расщепления соотношения и начального условия в случае обратимости на первом шаге. Получены условия существования, единственности решения задачи; найдено это решение в аналитическом виде. Доказывается фредгольмовость некоторого линейного оператора, что применяется в иллюстрирующем примере.

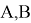
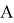
Ключевые слова: линейное рекуррентное соотношение, первый порядок, начальная задача, фредгольмов оператор, одношаговое расщепление.

Рассматривается задача:

(1)

(2)

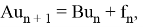
где

— линейные операторы: , — искомая последовательность из , a — заданный элемент из , — заданная ограниченная последовательность со значениями в ; .

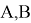
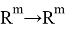
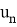
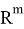
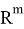
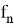
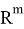
Под решением задачи (1), (2) подразумевается последовательность , определенная и удовлетворяющая (1), (2) при каждом .

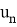
Основы теории рекуррентных соотношений (возвратных последовательностей) были разработаны и опубликованы в 20-х гг. XVIII в. французским математиком А. Муавром и швейцарским математиком Д. Бернулли. Развёрнутую теорию дал крупнейший математик XVIII в. петербургский академик Л. Эйлер. Из более поздних работ следует выделить изложение теории возвратных последовательностей в курсах исчисления конечных разностей, читанных знаменитыми русскими математиками академиками П. Л. Чебышевым и А. А. Марковым.

Рекуррентные соотношения играют большую роль в дискретной математике, являясь по существу в некотором смысле дискретным аналогом дифференциальных уравнений. Кроме того, они позволяют сводить данную задачу от n параметров к задаче от n — 1 параметров, потом к задаче от n — 2 параметров и т. д. Последовательно уменьшая число параметров, можно дойти до задачи, которую уже легко решить.

Рекуррентными соотношениями первого порядка и их системами описывается динамика частицы в вязкой среде под действием импульсных толчков (отображение Эно) [1], динамика лимитированной структурированной популяции при избирательном промысле [2] и т. д.

Здесь оператор A полагается вырожденным: . Его можно рассматривать как фредгольмов с нулевым индексом (далее, фредгольмов) [3]. Отметим, что в этом случае решение задачи (1), (2) существует не при каждом значении a . Рассматривается случай: . Определены условия существования и единственности решения и найдено это решение в аналитическом виде. Для этого используется метод каскадного расщепления исходной задачи на соответствующие задачи в подпространствах уменьшающихся размерностей.

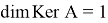
1. Необходимые сведения

Рассмотрим вспомогательную задачу:

(3)

(4)

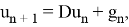
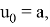
где — линейный оператор: , — искомая последовательность из , a — заданный элемент из , — заданная последовательность со значениями в ; .

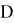
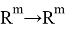
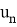
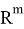
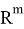
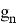
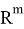
Имеет место следующая лемма.

Лемма 1. Решение задачи (4), (5) единственно и равно

(5)

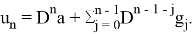
Доказательство. Методами функционального анализа [4] доказывается, что если оператор D ограничен, то задача имеет единственное решение.

Установим, что последовательность (5) является решением. Имеем:

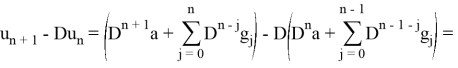
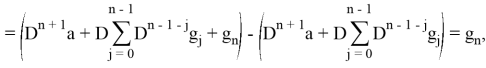
что и требовалось доказать.

Замечание 1 [5].Линейный оператор

, задаваемый вырожденной квадратной матрицей, фредгольмов.

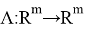
Этот результат в частном случае некоторого оператора будет доказан далее.

В силу замечания оператор A можно полагать фредгольмовым, что влечет разложения в прямые суммы:

(6)

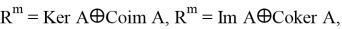
где — ядро, — прямое дополнение к ядру, — образ, — дефектное подпространство; .

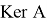
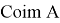
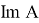
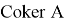
Для него введем проектор на , сужение оператора на , полуобратный оператор (здесь и далее, — единичный оператор в соответствующем подпространстве).

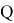
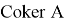
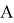
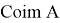
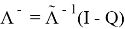
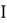
Пусть далее, оператор A имеет одномерное ядро. Зафиксируем элементы , ,

и в введем скалярное произведение так, что.

(7)

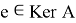
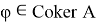
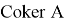
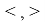
В работе [6] доказано следующее утверждение.

Лемма 2. Линейное уравнение равносильно системе

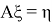
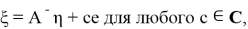
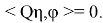
Перейдем к решению задачи, для чего докажем лемму о регуляризации соотношения (1) (то есть, сведения к виду (3)).

2. Решение начальной задачи

В силу леммы 2 соотношение (1) равносильно системе

(8)

(9)

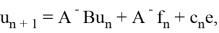
с искомой последовательностью .

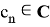
Заменив в (9)

на , получим

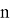
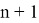
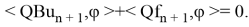
Подставив в полученное соотношение выражение (8), получим

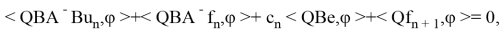
откуда

(10)

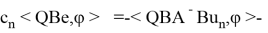
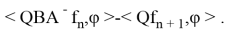
Далее, пусть выполнено условие.

Условие 1.

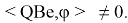
Выразив из (10) и подставив в (8), получим

(11)

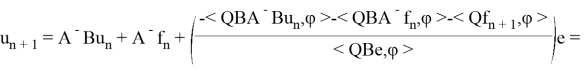
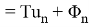
в обозначениях

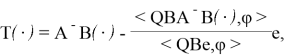
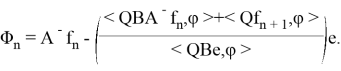
Тем самым, получен следующий результат.

Лемма 4. Пусть выполнено условие 1. Тогдасоотношение (1) равносильно системе (11), (9).

Имеет место предложение.

Предложение 1. Оператор ограничен, последовательность ограничена.

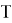
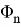
Операторы A , B ограничены, как действующие в . Применим неравенство Коши-Буняковского [4] для скалярного произведения, взяв некоторый элемент ( ):

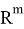
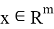
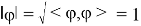
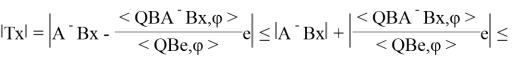
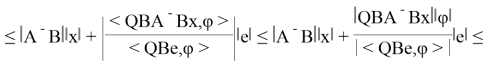
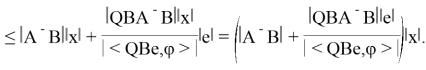
Это влечет ограниченность

. Аналогично доказывается что, в силу ограниченности , последовательность ограничена. Лемма доказана.

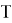
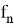
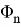
Из лемм 4, 1 и предложения 1 вытекает следующее утверждение.

Теорема 1. Пусть выполнено условие 1. Тогда решение задачи (1), (2) существует при выполнении условия

(12)

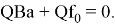
Оно единственно и определяется формулой

(13)

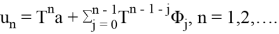
Это решение обладает свойством

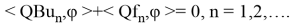
Условие (12) называется условием согласования.

3. О фредгольмовости одного оператора

Предложение 2. Оператор

фредгольмов.

Доказательство. Будем обозначать , элемент из некоторого подпространства G .

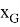
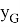
1. Вычислим ядро этого оператора, решив уравнение

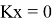
с искомым вектором и нулевым вектором Запишем уравнение как систему:

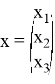
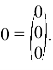
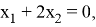
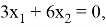
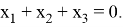
В этом системе возьмем одну из переменных — например, — в качестве параметра. Выразим в первом уравнении : и подставим в остальные: второе уравнение обратится в тождество 0 = 0, а третье примет вид: откуда Следовательно,

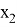
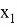
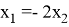
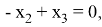
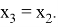
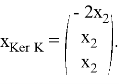
Разложим этот элемент по базису :

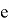
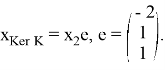
Отметим, что ядро одномерно.

2. Построим подпространство . Пусть и разложим в прямую сумму

(14)

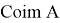
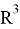
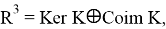
то есть, откуда

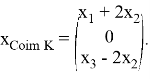
Докажем, что (14) является прямой суммой, для чего установим, что

. Приравняем эти элементы:

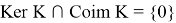
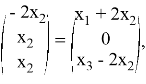
откуда из вторых компонент вытекает . Подставив это в первую и третью компоненты последнего равенства, получим , что и означает требуемое.

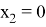
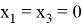
3. Построим образ . Для этого составим уравнение

, то есть, систему

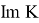
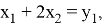
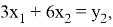
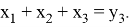
Заметим, что вторая строка в 3 раза больше первой: , а третья строка не зависит линейно от остальных, то есть,

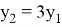
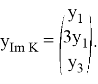
4. Теперь построим дефект . Пусть

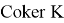
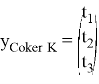
и разложим в прямую сумму

(15)

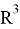
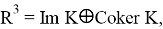
то есть, откуда

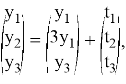
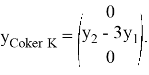
Разложим этот элемент по базису :

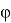
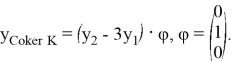
Отметим, что дефект одномерен, значит, условие равенства размерностей ядра и дефекта выполнено. Кроме того, имеет место (7).

Аналогично доказывается, что (15) является прямой суммой.

5. Вычислим оператор , для чего составим уравнение

, то есть,

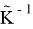
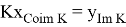
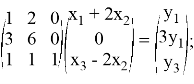
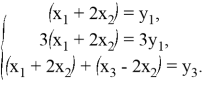
Из первого и второго равенства системы вытекает, что первая компонента . А из третьего равенства — что третья компонента этого элемента равна . Значит,

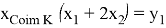
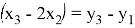
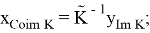
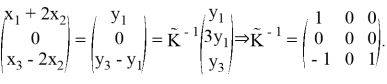
6. Построим проектор на : для этого составим уравнение

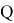
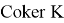
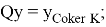
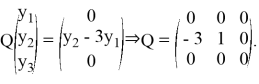
Проверяем, что — проектор: имеет место равенство , что влечет требуемое.

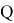
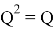
4. Пример

Рассматривается задача:

(16)

(17)

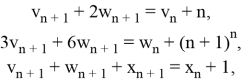
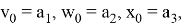
где , — заданные вещественные постоянные, .

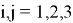
Система (16) — это соотношение (1) с операторами ,

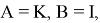
вектором , а условия (17) — это начальный вектор .

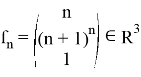
В предыдущем пункте было доказано, что оператор фредгольмов. Условие 1 выполнено: . Далее, равенство (12) — это

(18)

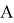
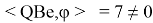
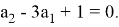
Вычислим оператор

и последовательность

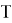
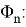
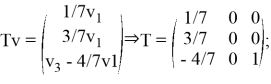
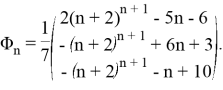
Рассмотрим частный случай , , , удовлетворяющий равенству (18), и выпишем первые три члена последовательности (13) , удовлетворяющей (16), (17):

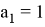
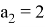
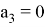
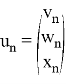
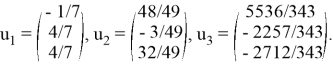
Литература:

1. Кузнецов С. П. Динамический хаос (курс лекций) / С. П. Кузнецов. ‒ Физматлит, 2001. ‒ 295 с.
2. Неверова Г. П. Режимы динамики лимитированной структурированной популяции при избирательном промысле / Г. П. Неверова, А. И. Абакумов, Е. Я. Фрисман // Математическая биология и биоинформатика. ‒ 2017. ‒ Т. 12. № 2. ‒ С. 327‒342.
3. Никольский С. М. Линейные уравнения в линейных нормированных пространствах / С. М. Никольский // Изв. АН СССР. Сер. матем. — 1943. — Т. 7, вып. 3. — С. 147‒166.
4. Функциональный анализ. — Под общ. ред. С. Г. Крейна. — М.: Наука, 1972.
5. Усков В. И. Решение задач для уравнений соболевского типа методом каскадной декомпозиции // Дисс… канд. физ.-мат. наук. — Воронеж, 2019. — 137 с.
6. Zubova S. P. Asymptotic Solution of the Cauchy Problem for a First-Order Equation with a Small Parameter in a Banach Space. The Regular Case / S. P. Zubova, V. I. Uskov // Mathematical Notes, 2018, Vol. 103, No. 3, p. 395 ‒ 404.