О решении одной смешанной задачи для уравнения плотности акций



Работа посвящена исследованию смешанной задачи для одного уравнения теплопроводности, описывающего плотность акции. Задача заключается в нахождении функции плотности акции в смешанной задаче на полуоси для вырождающегося уравнения теплопроводности. Получено явное решение рассматриваемой задачи.

Ключевые слова: смешанные задачи, параболическое уравнение, формула Пуассона.

The work is devoted to the study of a mixed problem for one heat conduction equation describing the stock density. The problem is to find the stock density function in the mixed problem on the semi axis for the degenerate heat equation. An explicit solution of the problem under consideration is obtained.

Keywords: mixed problems, parabolic equation, Poisson's formula.

Аналитическое моделирование основано на описании моделируемого объекта с помощью математических формул, которые выражаются через алгебраические, дифференциальные, а также интегральные уравнения и систем. При этом связывающие выходные и входные переменные модели, дополняются системой ограничений и целевой функцией. Причем, как правило, существует много способов получения аналитического (явного) решения уравнений.

Акция предприятия — ценная бумага (документ), означающая, что ее владелец является собственником доли предприятия, а стоимость акции означает стоимость этой доли. Таким образом, акция — это бумага специального назначения, которая имеет определенную рыночную стоимость. Естественно, в зависимости от экономической ситуации стоимость акции изменяется со временем. Акции продаются и покупаются на бирже и дают право получать дивиденды (доход) [1, с. 19].

Стоимостью обладают и другие объекты: любые виды товара на рынке, иностранная валюта, долговые бумаги, контракты. Все виды объектов, имеющих стоимость, покупающихся и продающихся на рынке в большом количестве, называются активом соответствующего вида. Актив — это или акции, или товар, или иностранная валюта, или банковские счета, или облигации, или контракты и т. д. [1, 2].

Для активов предпринимателями заключаются разного рода финансовые договоры, контракты, обязательства и они оформляются в виде документов (ценных бумаг), которые также обладают определенной стоимостью. Такие ценные бумаги называются финансовыми производными от исходного актива.

Этот процесс математически выражается следующим уравнением параболического типа и

.(1)

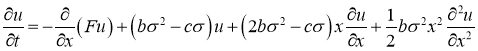
Уравнение (1.1) фактически является нелинейным уравнением и строгий вывод этого уравнения изложено в работе [4].

Мы упростим это уравнение.Введем обозначение . Тогда уравнение (1) приобретает вид

, , (2)

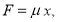
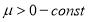
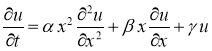
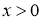
где

,

, . (3)

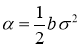
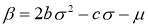
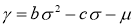
Уравнение (2) называется уравнением для плотности акций и является вырождающимся уравнением теплопроводности. Запишем это уравнение в дивергентном виде:

. (4)

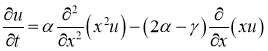
Из этой формы записи можно получить закон сохранения числа акций на пространстве цен. Действительно, интегрируя уравнение (4) по в пределах от до , получаем

.

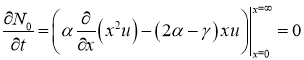
Следовательно, , то есть число акций на пространстве цен не зависит от времени .

2. Постановка задачи и основной результат

В областирассмотрим следующую задачу для параболического уравнения

в (5)

,

(6)

,(7)

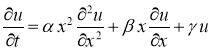
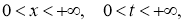
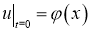
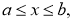
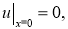
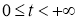
где , , .

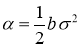
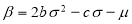
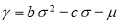
Задача (5)–(7)означает, что в начальный момент времени акции распределены на полуоси и известна функция плотности их распределения

. Требуется определить плотность акций из уравнения (5) в последующие моменты времени .

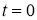
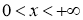
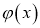
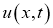
Уравнение (5) имеет две особенности, во-первых, уравнение является вырождающимся, во-вторых, имеется младшие члены, которые не позволяют непосредственно применить функцию Грина. Для этого введем новую неизвестную функцию , производя замену , тогда относительно функции получим задачу

,(8)

,

(9)

.(10)

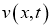
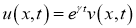
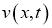
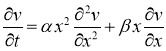
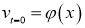
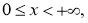
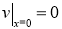
Далее произведем замену независимых переменных , вводя новые переменные :

, , .

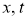
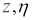
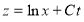
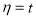
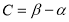
Вычислим производные

, , .

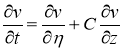
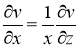
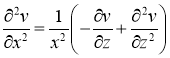
Подставляя найденные производные в уравнение (8) вместо задачи (8) -(10), получим задачу Коши для уравнения теплопроводности:

(11)

, ,(12)

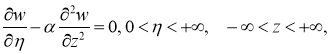
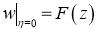
где

, , .

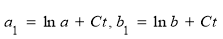
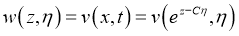
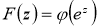
Решение задачи (11), (12) можно выписать явно [3]:

.

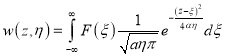
Пусть , . Тогда получим

.

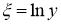
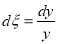
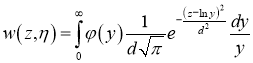
Теперь возвращаясь к старым переменным, получим решение исходной задачи (5) -(7):

. (13)

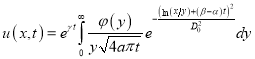
Пример 1. Рассмотрим пакет из акций, каждая из которых в момент времени стоила ден.единиц. Тогда начальная плотность акций в условии (12) может быть представлена в виде

,

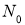
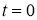
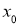
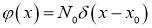
где — дельта-функция Дирака, сосредоточенная в точке.

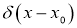
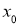
Так как Дельта функция Дирака является обобщенной функцией, то нам удобно использовать следующие свойства Дельта функции

.(14)

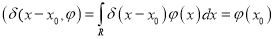
Подставляя в формулу (13) и используя (14), находим

. (15)

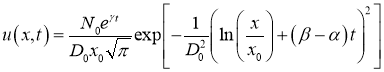
Функцию (15) при можно интерпретировать как плотность вероятностей, с которой будет распределена цена одной акции в момент времени при условии, что в начальный момент времени акция стоила

денежных единиц.

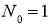
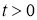
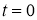
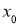
Литература:

1. Медведев Г. А. Математические модели финансовых рисков. Минск: БГУ, 1999. Ч. 1.
2. Математические и инструментальные методы в современных экономических исследованиях:Монография / Под редакцией М. В. Грачевой и Е. А. Тумановой.
3. Тихонов А. Н. Самарский А. А. Уравнения математической физики. М.: Наука, 1972.- 735с.
4. Ерофеенко В. Т., Козловская И. С. Уравнения с частными производными и математические модели в экономике: Курс лекций. МИНСК. 2004.-246с.