У современного ученика, который заканчивает 9 класс, стоит серьёзный выбор: пойти в колледж или же продолжить обучение в школе. Многие ученики после окончания среднего общего образования выбирают роль студента-первокурсника в колледже, для освоения профессии. Учебные нагрузки, которые «кардинально» отличаются от школьной, нередко травмируют студента–первокурсника, что сказывается негативным образом на процессе адаптации в колледже.
Проблема адаптации пристально изучается с момента переориентации системы образования в сторону гуманизации и реализации индивидуального подхода к обучению. Данной проблемой занимались следующие исследователи: Г. В. Безюлева, С. В. Васильева, Т. Д. Дубовицкая, Н. Г. Колызаева, И. В. Коровина, С. Т. Посохова.
В психологии принято следующее определение: «адаптация — приспособление к изменяющимся внешним и внутренним условиям», то есть адаптацию можно определить, как процесс установления оптимального соответствия личности и внешнего мира в ходе деятельности человека, которая удовлетворяет потребности в достижении поставленных целей, обеспечивая соответствие психической деятельности человека и его поведения требованиям среды.
По мнению И. В. Коровиной, можно различать следующие виды адаптации студента:
— адаптацию к условиям учебной деятельности (приспособление к новым формам преподавания, контроля и усвоения знаний, к иному режиму труда и отдыха, самостоятельному образу жизни и др.);
— адаптацию к учебной группе (включение в коллектив сокурсников, усвоение его правил, традиций);
— адаптацию к будущей профессии (усвоение профессиональных знаний, умений и навыков, качеств).
Успешность адаптации зависит от преодоления различных трудностей студента-первокурсника, которые возникают в процессе обучения и общения с однокурсниками. Значимым фактором так же является проявление активной позиции студента, студент должен сам стремиться находить и выбирать для себя способы и пути достижения образовательной цели. Уровень представлений студента о профессии (адекватный или неадекватных) непосредственно соотносится с уровнем его отношения к учебе: чем меньше студент знает о профессии, тем ниже у него положительное отношение к учебе.
Из вышесказанного следует, что необходима целенаправленная работа каждого преподавателя для создания оптимальных условий адаптации студентов-первокурсников. Особенно это важно при изучении базовых предметов, среди которых важное место занимает математика: как для развития способностей решать разноплановые задачи, так и для развития умения эффективно использовать вычислительную технику. Большинство производственных технических, экономических, компьютерных задач могут быть решены на основе математических знаний. Математика — это основа в развитии таких важных качеств личности, как умение мыслить логически, анализировать, чётко и сжато выражать свои мысли.
Таким образом, преподаватель математики должен разработать особые методические подходы при обучении студентов-первокурсников в первом семестре.
Для нахождения и создания таких методических подходов необходимо знать исходное состояние как уровня адаптированности поступивших студентов, так и уровень их знаний по математике. Важно выявить их проблемы на наиболее раннем этапе. Поэтому в начале учебного года студентам-первокурсникам предлагаются анкета и тест, позволяющие понять проблемы, мотивы, уровень адаптации и уровень знаний по предмету. Нами были разработаны следующие анкета и тест.
Анкета
Выберите один или несколько ответов на каждый вопрос.
1. Какие факторы сыграли решающую роль в выборе вами специальности? Выберите, на ваш взгляд, главное.
А) Мнение и рекомендации родителей
Б) Советы или пример друзей или родственников
В) Личная склонность к определённому виду деятельности
Г) Престижность специальности
Д) Свой вариант______________________________
2. С какой целью Вы поступили в колледж?
А) Избежать ЕГЭ по математике
Б) Начать зарабатывать по специальности
В) Получить профессиональные знания по специальности.
Г) Получить образование до армии
Д) Настояли родители
Е) Решил(а) пойти вместе с друзьями
Ж) Свой вариант______________________________
3. Испытывали ли Вы трудности в адаптации к студенческой жизни?
А) да, испытывал некоторые сложности, трудно было в начале обучения;
Б) да, испытываю некоторые проблемы к адаптации в вузе до сих пор
В) нет, не испытывал никаких трудностей.
4. Кто (что) помогло адаптироваться к обучению?
А) Желание учиться
Б) Школьная привычка учиться
В) Советы и помощь куратора учебной группы и / или сотрудников деканата
Г) Адресная помощь и поддержка представителей администрации
Д) Сотрудничество в группе
Е) Доброжелательное взаимодействие с преподавателями
Е) Культурно-досуговая деятельность
Ж) Свой вариант_____________________________________________
5. Какие трудности возникли у Вас при обучении в колледже?
А) Не умею конспектировать
Б) Не успеваю усваивать материал, нужно больше времени
В) Не умею работать с учебной, справочной литературой
Г) Не умею писать доклады, рефераты, сообщения
Д) Не умею работать самостоятельно
Е) Свой вариант_____________________________________________
6. Нравится ли Вам предмет «Математика»? Почему?
А) Нравится, так как учитель интересно преподаёт
Б) Нравится, потому что легко даётся
В) Не нравится
Г) Свой вариант______________________________
7. Что Вам больше всего нравится на уроке математики
А) Лекционные занятия, объяснение материала
Б) Семинарские занятия, решение алгебраических задач
В) Семинарские занятия, решение геометрических задач
Г) Самостоятельная работа
Д) Работа с учебником
Е) Поиск информации в сети Интернет
Ж) Работа в паре
З) Творческая работа на уроке
И)Свой вариант______________________________
8. Как Вы ведёте себя на занятиях по математике? Оцените себя по пятибалльной системе (от «0» — низий уровень до «5» — высокий уровень)
А) Готовность к уроку_______;
Б) Внимание ________;
В) Дисциплина ________
Г) степень усвоения программы ________;
9. Оцените свои знания по предмету математика
А) Очень плохие знания
Б) Плохие знания
В) Средние знания
Г) Выше среднего знания
Д) Отличные знания
10. Стремитесь ли вы улучшить результаты своей учёбы по математике?
А) Да
Б) Нет
11. Как вы считаете, в чём для Вас заключается сложность в изучении математики?
А) Не умею находить значение алгебраических выражений
Б) Не умею решать текстовые или геометрические задачи
В) Не умею применять изученную теорию (определения, правила, теоремы, свойства) к решению задач (примеров)
Г) Недостаточное количество занятий
Д) Недостаточно раскрыт материал на уроке
Е) Недостаточно справочной литературы
Ж) свой вариант_____________________________________________
12. Что вы делаете, когда у вас не знаете, как решить «проблему»?
А) Использую ГДЗ
Б) Использую учебники, справочную или дополнительную литературу по предмету
В) Использую помощь репетитора
Г) Использую помощь учителя по предмету
Д) Свой вариант______________________________
13. Какая помощь и с чьей стороны Вам нужна, чтобы справиться с трудностями? ___________________________________________________
14. Что бы Вы изменили на занятии по математике?
А) Увеличить количество уроков
Б) Уменьшить количество уроков
В) Больше работать с компьютерными обучающими программами
Г) Проводить ещё больше практических работ
Д) Больше материала изучать самостоятельно
Е) Увеличить наглядность преподавания
Ж) Свой вариант______________________________
15. Хотели бы Вы принимать участие во внеурочных мероприятиях по математике?
А) Да, так как хочу найти применение своим знаниям
Б) Да, так как хочу совершенствовать свои знания
В) Да, хочу развить артистические способности
Г) Нет
Обработка результатов:
Обработка результатов осуществляется путем перевода высказываний в +, -, 0, где в последствии значения будут суммироваться. Исходя из большего количества +, — или 0 будет делаться следующий вывод:
|
Положительная адаптация (+) |
Частичная адаптация (0) |
Низкая (отрицательная) адаптация (-) |
|
студенты успешны, ярко выражен интерес к учебе и коллективом, не имеют признаки утомления учебным процессом. Положительное отношение к различным аспектам деятельности и общения и к себе самому (стремление к совершенствованию, желание самореализации, ведущие ценностные ориентации и их организация, отношение к риску, оценку своих возможностей, эмоциональную стабильность личности) |
студенты удовлетворены коллективом и учебным процессом, равнодушны к выбору профессии. Проявляют спокойствие и не выражают ярких стремлений. Студент частично изменяется и перестраивается внутренне под среду, ее ценности, нормы и в то же время частично адаптируется инструментально, поведенческий, сохраняя свое «Я» и самостоятельность. |
студенты, испытывающие трудности в адаптации к группе и к учебной деятельности; |
После анкетирования, предлагается входной контроль по математике основанный на базовом уровне ОГЭ.
Тест по математике
1.
Вычислите:
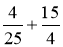
Решение.
Приведём дроби к общему знаменателю:
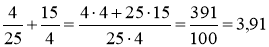
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Получен верный ответ |
2 |
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
1 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
0 |
|
Другие случаи, не соответствующие указанным критериям. |
2.
Решите уравнение
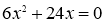
Решение.
Последовательно получаем:
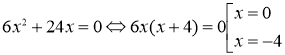
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Получен верный ответ |
2 |
|
Ход решения верный, все шаги выполнены правильно, дан верный ответ. |
1 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
0 |
|
Другие случаи, не соответствующие указанным критериям. |
3.
Втреугольнике
ABC
угол
C
равен 90°,
BC
= 20,
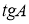
Решение.
Тангенс угла равен отношению противолежащего углу катета к прилежащему:
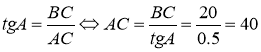
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Получен верный ответ |
2 |
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
1 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
0 |
|
Другие случаи, не соответствующие указанным критериям. |
4.
На окружности с центром
O
отмечены точки
A
и
B
так, что
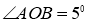
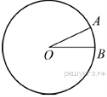
Решение.
Пусть длина большей дуги АВ равна х. Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
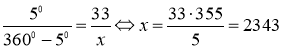
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Правильно составлено уравнение, получен верный ответ |
2 |
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
1 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
0 |
|
Другие случаи, не соответствующие указанным критериям. |
5. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 24 и HD = 2. Найдите площадь ромба.
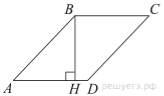
Решение.
Из прямоугольного треугольника
ABH
найдём
BH
:
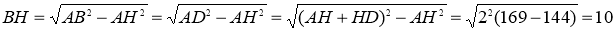
Площадь ромба можно найти как произведение основания на высоту:
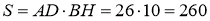
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Правильно составлено уравнение, получен верный ответ |
2 |
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
1 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
0 |
|
Другие случаи, не соответствующие указанным критериям. |
6.
Решите уравнение
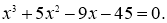
Решение.
Раскладывая на множители левую часть уравнения, получаем
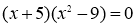
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Правильно выполнены преобразования, получен верный ответ |
2 |
|
Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
Максимальный балл |
2 |
7. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решение.
Пусть x км — расстояние, которое проехал первый велосипедист до места встречи, x>0 , тогда 82-x км — расстояние, которое проехал второй велосипедист до места встречи.
Составим таблицу по данным задачи:
|
Скорость, км/ч |
Время, ч |
Расстояние, км |
|
|
Первый велосипедист |
28 |
x/28 |
x |
|
Второй велосипедист |
10 |
(82-x)/10 |
82-x |
Так как первый велосипедист сделал остановку на 3/5 ч., составим уравнение:
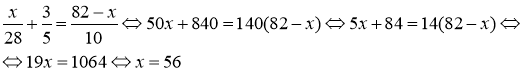
Таким образом, второй велосипедист проехал 82 − 56 = 26 км до места встречи.
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Правильно составлено уравнение, получен верный ответ |
2 |
|
Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа |
1 |
|
Другие случаи, не соответствующие указанным критериям |
0 |
8 . Точка H является основанием высоты BH , проведённой из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH , если PK = 12.

Решение.
Угол РВК — вписанный, он равен 90° и опирается на дугу КНР следовательно, дуга КНР равна 180°, значит, хорда РК — диаметр окружности и ВН=РК=12
Критерии проверки:
|
Критерии оценивания выполнения задания |
Баллы |
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
2 |
|
Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. |
1 |
|
Другие случаи, не соответствующие указанным критериям. |
0 |
|
Максимальный балл |
2 |
Обработка результатов:
зона высокой адаптации — 16–13 баллов;
зона нормальной адаптации — 12–9 баллов;
зона низкой адаптации- 8–5 баллов;
зона дезадаптации — 0–4 баллов.







