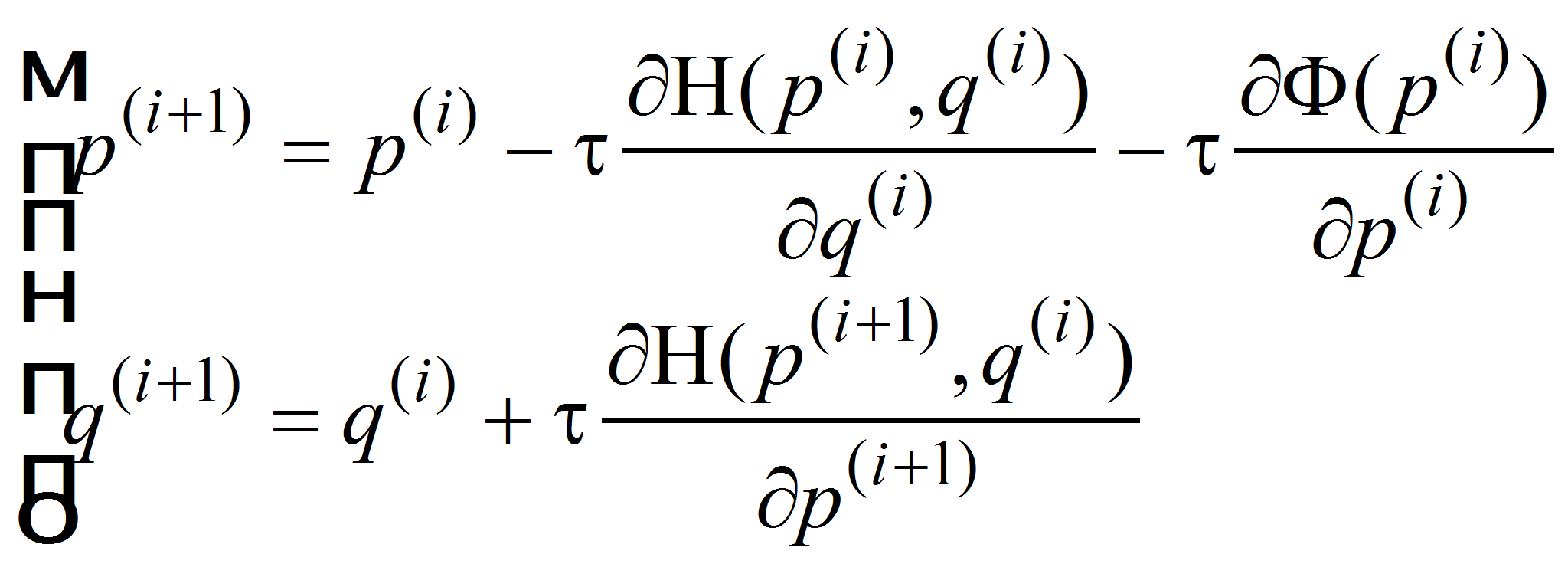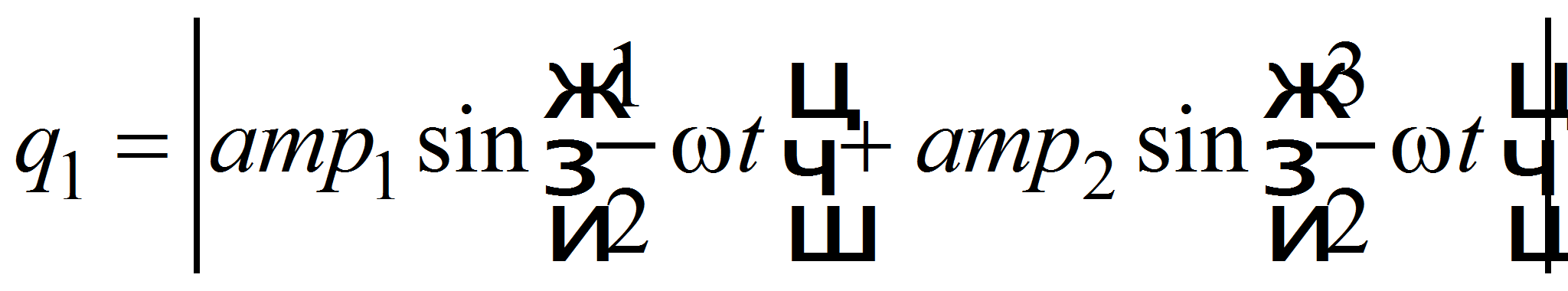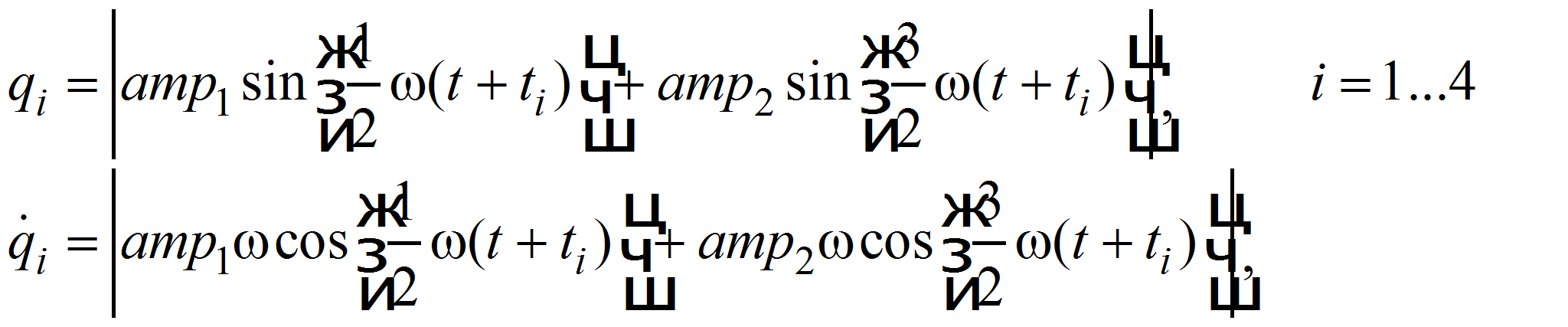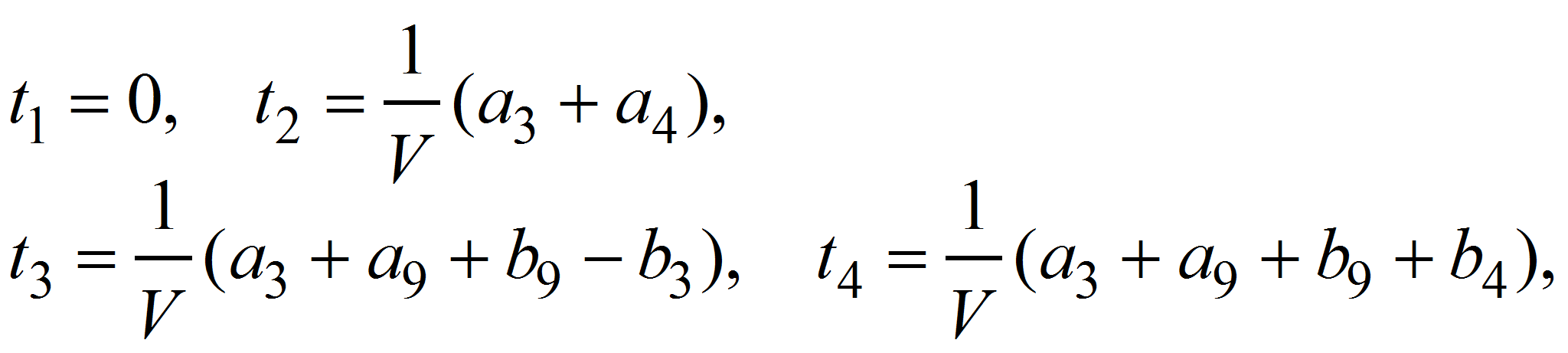Взаимодействие вагона и железнодорожного пути представляет собой сложную для исследования задачу [1]. В реальных условиях рельсы и колеса имеют неровности на поверхности качения, а также другие технологические особенности, в результате чего, в элементах железнодорожного пути и подвижного состава возникают колебания. Актуальность решения определяется изменениями условий эксплуатации железнодорожного транспорта.
Для решения задач, которые имеют большую размерность и включают нелинейности, целесообразно использовать математическое и компьютерное моделирование. Компьютерное моделирование включает в себя построение математической модели и численный эксперимент, который обходится дешевле, чем натурный эксперимент. Компьютерный эксперимент не отменяет натурный эксперимент, а дополняет его, позволяя получить больше информации об исследуемом процессе, и при этом стоит намного дешевле, чем натурный.
Безопасность движения поездов, ритмичность и рентабельность работы железнодорожного транспорта существенно зависит от конструкции и состояния железнодорожного пути и подвижного состава. Колебания железнодорожного вагона при движении по неровному железнодорожному пути оказывают влияние на состояние пассажиров. Колебания снижают эксплуатационные характеристики вагона, отражаются на сохранности перевозимого груза. Поэтому, одним из основных требований, предъявляемыми к современному транспорту являются повышение плавности хода и улучшение комфортабельности езды [2].
Действие колебаний на организм человека зависит от частоты, амплитуды, продолжительности действия и направления. Влияние знакопеременных ускорений на организм человека, в большей степени, зависит от частоты колебаний. С увеличением частоты, даже небольшие ускорения колебаний могут вызвать неприятные ощущения и даже нанести вред здоровью пассажира.
Железнодорожный путь и подвижный состав, в частности железнодорожный вагон, представляют единую механическую систему. Железнодорожный выгон как колебательную систему, можно представить в виде системы сосредоточенных абсолютно твёрдых инерциальных элементов (масс), соединённых безинерциальными упругими элементами и демпфирующими элементами, обеспечивающими рассеивания энергии при колебаниях. Ограничения, накладываемые на перемещения или скорости элементов системы, называются связями [3]. Связи могут осуществляться направляющими устройствами (рельсовая колея), шарнирными элементами, упругими и диссипативными элементами (пружины, рессоры, резиновые элементы, гасители колебаний).
В отличие от известных подходов, математическую модель объекта запишем в виде системы уравнений Гамильтона [4]. Данный подход показал свои преимущества в моделировании и исследовании прикладных задач [5].
Исследуем влияние неровного пути на водителя и частей железнодорожного состава, в качестве элемента которого был выбран (рис. 1).
Рис. 1. Пассажирский вагон
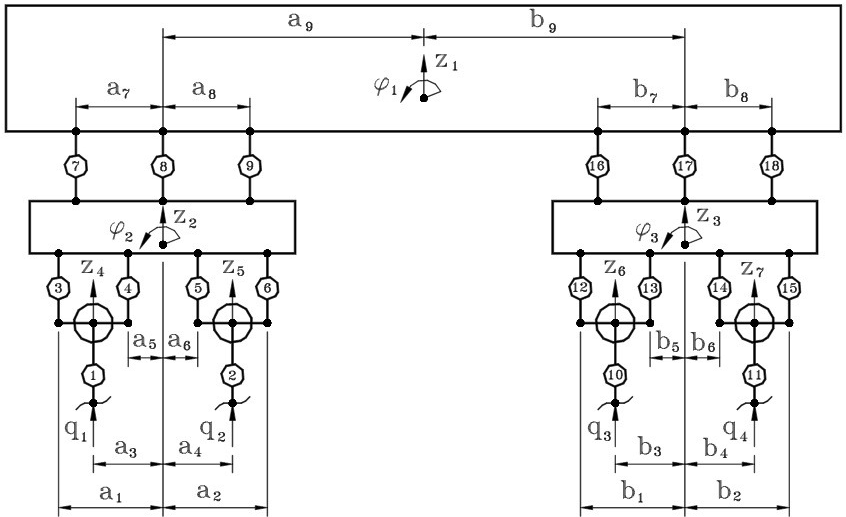
Расчетная схема железнодорожного вагона состоящего из платформы, двух тележек с буксовым под рессорным подвешиванием, колесных пар, представлена на рис. 2 [6].
Рис. 2. Расчетная схема вагона
Пусть система находится под действием потенциальных и диссипативных сил. Уравнения движения имеют вид системы уравнений Гамильтона:
|
(1) |
|
|
(2) |
![]() – кинетическая и потенциальная энергия;
– кинетическая и потенциальная энергия;
![]() –
соответственно
векторы обобщённых координат и импульсов.
–
соответственно
векторы обобщённых координат и импульсов.
Векторы обобщенных
координат
![]() и импульсов
и импульсов
![]() имеет следующий вид:
имеет следующий вид:
|
(3) |
Для численного интегрирования системы (1) воспользуемся каноническим методом интегрирования алгоритмом вида импульс-координата [7]:
|
(4) |
Кинетическая энергия вагона определяется следующим отношением:
|
(5) |
где: ![]() ,
,
![]() – масса и момент инерции массы
– масса и момент инерции массы
![]() -го
тела;
-го
тела;
![]() ,
,
![]() – обобщенные скорости
– обобщенные скорости
![]() -го
тела.
-го
тела.
Потенциальная энергия
![]() и
диссипативная функция
и
диссипативная функция
![]() определяются следующими соотношениями:
определяются следующими соотношениями:
|
(6) |
и для
![]() -элемента
приведены в таблице 1.
-элемента
приведены в таблице 1.
Таблица 1
Потенциальная энергия
![]() и диссипативная функция
и диссипативная функция
![]() для
для
![]() -эл.
-эл.
|
Номер элемента |
||
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
10 |
||
|
11 |
||
|
12 |
||
|
13 |
||
|
14 |
||
|
15 |
||
|
16 |
||
|
17 |
||
|
18 |
где
![]() – коэффициент жесткости и
– коэффициент жесткости и
![]() – коэффициент демпфирования
– коэффициент демпфирования
![]() -эл.
-эл.
Исходные данные для построения компьютерной модели приведены в таблицах 2,3.
Таблица 2
Массы и моменты инерции элементов вагона
|
№ элемента i |
Название элемента |
Масса, m, кг |
Момент инерции, I, кг∙м2 |
|
1 |
Платформа |
27140 |
90000 |
|
2 |
Тележка №1 |
2791 |
3000 |
|
3 |
Тележка №2 |
2791 |
3000 |
|
4 |
Колесная пара №1 |
1013 |
- |
|
5 |
Колесная пара №2 |
1013 |
- |
|
6 |
Колесная пара №3 |
1013 |
- |
|
7 |
Колесная пара №4 |
1013 |
- |
Таблица 3
Кинематические и геометрические характеристики элементов вагона
|
№ элемента i |
Параметры демпфирующих элементов |
Расстояния между центром масс |
||
|
Коэффициент |
Обозначение |
Величина, м |
||
|
1 и 2 |
0 |
a1 и a2 |
1,49 |
|
|
3 и 4 |
a3 и a4 |
1,2 |
||
|
5 и 6 |
a5 и a6 |
0,91 |
||
|
7 и 8 |
a7 и a8 |
0,447 |
||
|
9 |
a9 |
9,625 |
||
|
10 и 11 |
0 |
b1 и b2 |
1,49 |
|
|
12 и 13 |
b3 и b4 |
1,2 |
||
|
14 и 15 |
b5 и b6 |
0,91 |
||
|
16 и 17 |
b7 и b8 |
0,447 |
||
|
18 |
b9 |
9,625 |
||
Траектория движения колеса на стыках железнодорожного пути может быть аппроксимирована следующим выражением:
|
(7) |
где: ![]() ,
,
![]() – амплитуды неровностей;
– амплитуды неровностей;
![]() – частота воздействия
стыков пути на вагон, движущийся со скоростью
– частота воздействия
стыков пути на вагон, движущийся со скоростью
![]() .
.
|
(8) |
При движении транспортного средства на каждую колесную пару неровность пути воздействует кинематически через определенные моменты времени, тогда для перемещений и скоростей точек колес справедливо:
|
(9) |
Определим время запаздывания для положения колесных пар:
|
(10) |
Таблица 4
Характеристики железнодорожного пути и скорость движения вагона
|
Название |
Обозначение |
Значение |
|
Длина рельса |
|
12,5 м |
|
Амплитуда первой гармоники |
|
20∙10-3 м |
|
Амплитуда второй гармоники |
|
10∙10-3 м |
|
Частота воздействия стыков пути на вагон |
|
16,75 с-1 |
|
Скорость движения вагона |
|
120 км/ч = 33,33 м/с |
|
Время моделирования |
|
5000 с. |
|
Шаг интегрирования |
|
0,01 |
Для оценки плавности хода для характерных точек подрессоренной части найдём среднеквадратичное значение вертикальных виброускорений которые не должны превосходить предельных значений [] ГОСТ 31191.1-2004 и ГОСТ 31248-2004.
|
(11) |
Неравенство (11) позволяет оценивать плавность движения вагона с учётом его конструктивных особенностей, вязких, упругих, массовых характеристик режима движения и состояния железнодорожного пути.
C помощью выражения (7) возможно моделирование различных типов железнодорожных путей. В статье рассматриваются колебания вагона в вертикальной плоскости при движении через единичную неровность и движение по неровному железнодорожному пути.
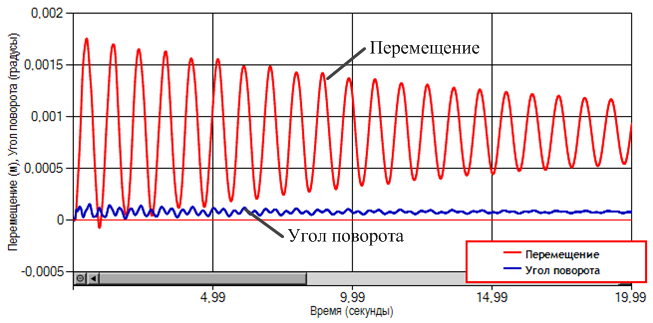
Исследуем движение вагона через единичную неровность железнодорожного пути. Под единичной неровностью здесь понимаем испорченный участок железнодорожного пути. На рисунке 3 представлены зависимости перемещения и угла поворота платформы железнодорожного вагона от времени, а на рисунке 3 представлена зависимость линейного и углового ускорения платформы железнодорожного вагона от времени.
Рис. 3. Зависимости перемещения и угла поворота платформы
вагона от времени, при скорости движения V=120 км/ч
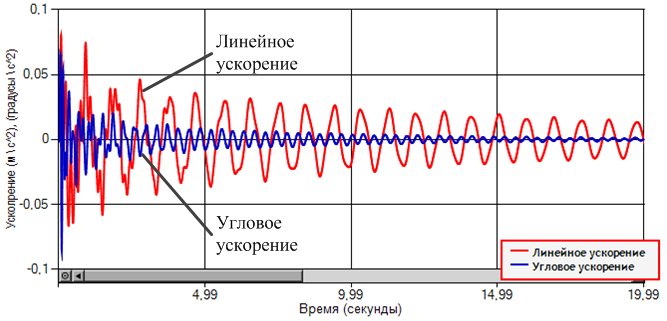
Рис. 4. Зависимости линейного и углового ускорений платформы
вагона от времени, при скорости движения V=120 км/ч
Были получены среднеквадратические виброускорения платформы железнодорожного вагона движущегося по единичной неровности железнодорожного пути, которые сравним с предельными значениями, взятыми из ГОСТа. Допустимое значение от 0 до 50 дБ. Линейное виброускорение 0,01303 м/c2 = 37,70402 дБ. Угловое ускорение 0,00451 м/c2 = 46,90863 дБ. Исследуем движение вагона по неровному железнодорожному пути, заданному по формуле (9).
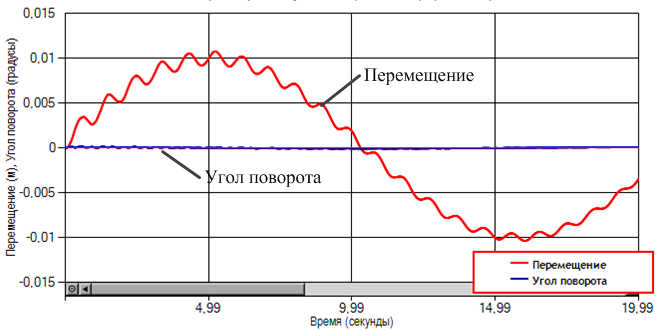
На рис. 5 представлены зависимости перемещения и угла поворота платформы железнодорожного вагона от времени, а на рисунке 6 представлена зависимость линейного и углового ускорения платформы железнодорожного вагона от времени.
Рис.5. Зависимости перемещения и угла поворота платформы
вагона от времени, при скорости движения V=120 км/ч
Рис. 6. Зависимости линейного и углового ускорений платформы
вагона от времени, при скорости движения V=120 км/ч
Были получены среднеквадратические виброускорения платформы железнодорожного вагона движущегося по единичной неровности железнодорожного пути, которые сравним с предельными значениями взятыми из ГОСТ. Допустимое значение от 0 до 50 дБ. Линейное виброускорение 0,01423 м/c2 = 36,93650 дБ. Угловое ускорение 0,00453 м/c2 = 46,87177 дБ.
Проведенный анализ движения железнодорожного состава по неровному пути и выполненные компьютерные эксперименты позволяют исследовать устойчивость движения, безопасность и комфортабельность передвижения пассажиров и сохранность перевозимых грузов.
Расчеты позволили проанализировать влияние некачественного железнодорожного пути на характер колебаний и безопасность движения железнодорожного состава.
-
- Литература:
Гарг В.К., Дуккипати Р.В. Динамика подвижного состава. / Под ред. Н.А. Панькина. – М.: Транспорт, 1988.
Благодарный Ю.Ф. Вибрационная безопасность. // Автомобил. пром-сть. – 2004. – № 7. – С. 38-39.
Шестаков А.А., Голечков Ю.И. Устойчивость и безопасность движения транспортных динамических систем. // Наукоемкие технологии. – 2007. – № 7. – С. 56–60.
Морозов Е.А. Каноническое интегрирование гамильтоновых систем. – Екатеринбург; Ижевск: Изд-во Института экономики УРО РАН, 2006. – 196 с.
Селиванов К.М. Канонический метод интегрирования в исследовании движения твердого тела. // Интеллектуальные системы в производстве. 2010. – № 1 Ижевск: Изд-во ИжГТУ С. 67–76.
Аладьев В.З., Богдявичюс М.А. Maple 6: Решение математических, статических и инженерно-технических задач. – М.: Лаб. базовых знаний, 2001. – 850 с.
Ефимов И.Н., Морозов Е.А. Каноническое интегрирование динамических систем. – Екатеринбург–Ижевск: Изд-во Института экономики УрО РАН, 2006. – 198 с.