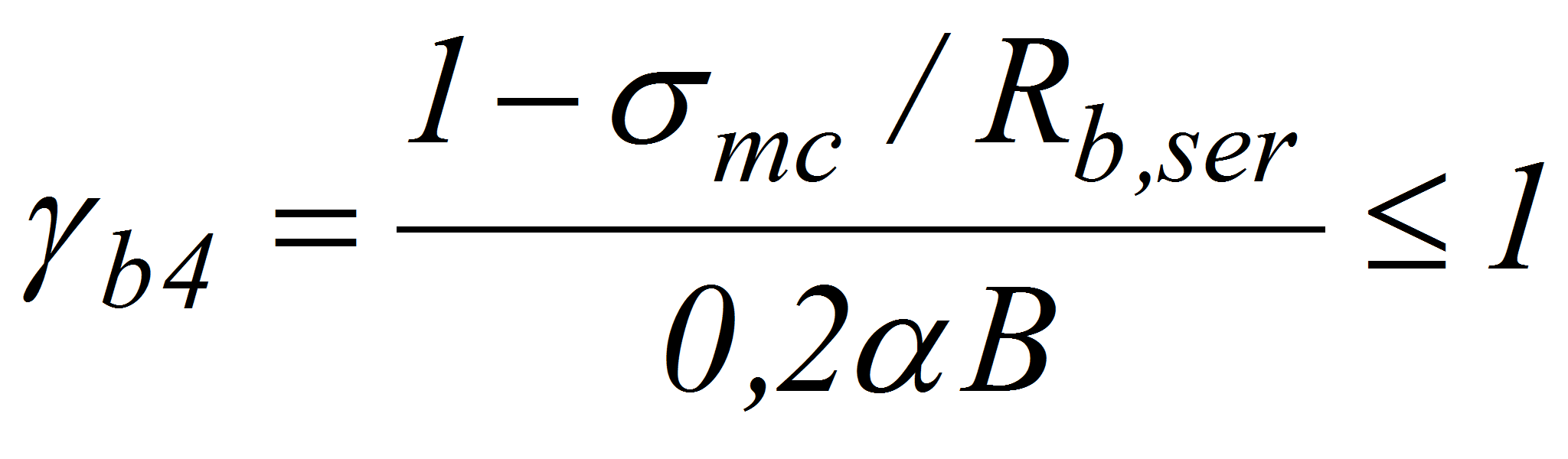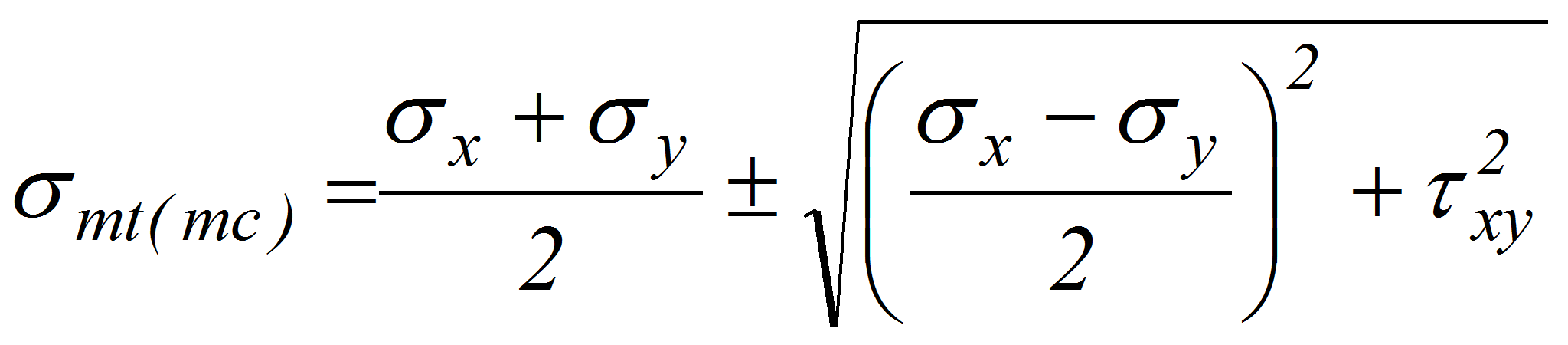Проектировать бетонные элементы, в которых от действия силовых факторов возникают растягивающие напряжения, не разрешается, поскольку образование трещины в подобном элементе приводит к его немедленному разрушению. По этой причине при проектировании необходимо всегда гарантировать превосходство прочности армированного железобетонного элемента над прочностью аналогичного бетонного элемента. Кроме того, сопротивление бетонного элемента является составной частью сопротивления образованию трещин обычного и предварительно напряженного железобетонного элемента. По указанным причинам исследование прочности бетонных элементов при наличии кручения приобретает актуальное значение.
При расчете крутильной прочности бетонных элементов и расчете усилий образования трещин в железобетонных элементах существует два подхода, основанных на классических теориях: теории упругости и теории пластичности. Первая рассматривает бетон как упругий материал, вторая - как полностью пластичный.
Идеи всех предложений, основанных на упругой теории, можно выразить одной формулой
Tb=KADt, (1)
где K - коэффициент, зависящий от формы поперечного сечения; A - площадь
поперечного сечения; D - диаметр вписанной окружности; t - максимальное касательное напряжение.
Для элементов прямоугольного сечения K зависит от отношения высоты сечения к ее ширине. Для элементов открытого профиля (тавровое, двутавровое, Г-образное) этот коэффициент получен на основе гипотезы Баха, согласно которой их сопротивление равно сумме сопротивлений отдельных прямоугольников. Такой подход дает удовлетворительные результаты только в случаях, когда сечение составлено из узких прямоугольников.
При расчете по пластической теории прочность бетонных элементов оценивается по формуле
Tb=Rbt W pl, (2)
где Wpl - пластический момент сопротивления, определяемый как удвоенный объем “кучи песка”, образующегося на сечении.
Обычно расчет по упругой теории занижает, а по пластической - завышает крутильную прочность бетонного элемента. На самом деле, как известно, бетон является упруго-пластичным, что и является причиной расхождения между опытными и теоретическими результатами.
Свой подход к этой проблеме СНиП [5] регламентирует в указаниях по расчету образования наклонных трещин. Согласно СНиП расчет по образованию трещин, наклонных к продольной оси элемента трещин, рекомендуется производить из условия
smt £ gb4 Rbt,ser, (3)
где gb4 - коэффициент условий работы бетона, определяемый по формуле
где a - коэффициент, зависящий от вида бетона; B - класс бетона по прочности на осевое сжатие, МПа.
Значения главных растягивающих напряжений в бетоне определяются по известной формуле сопротивления материалов
В этой формуле напряжения sx, sy и txy определяются как для упругого тела, за исключением касательных напряжений от действия крутящего момента, определяемых по формулам для пластического состояния элемента. Такой подход нельзя признать последовательным.
При кручении и изгибе с интенсивным кручением отсутствие арматуры какого-либо направления приводит к разрушению с появлением первой трещины, т.е. носит характер разрушения бетонного элемента. Это означает, что железобетон при кручении после появления трещин, представляет собой блочно-стержневую систему, в которой арматура работает на растяжение, а бетон - на сжатие. Отсутствие арматуры одного из направлений превращает систему в геометрически изменяемую, что и является причиной разрушения с появлением первой наклонной трещины.
Несколько иначе ведет себя железобетонная балка с продольной арматурой при интенсивном изгибе с кручением. В этом случае разрушение несколько отодвигается и появление наклонной трещины не приводит к немедленному разрушению. Причиной подобного поведения является то, что изгиб создает сжатую зону бетона, которая, взаимодействуя с продольной арматурой, еще сопротивляется кручению. Однако и в этом случае разрушение носит хрупкий и неожиданный характер, и проектировать такие конструкции не рекомендуется. Большое количество экспериментальных исследований, проведенных за рубежом, посвящено изучению поведения именно таких элементов, что несколько снижает их научную ценность при изучении прочности. Правда, данные указанных исследований, могут быть использованы при разработке метода расчета на образование трещин.
В момент разрушения бетонный элемент подвергается изгибу в плоскости, проходящей под углом 45o и продольной оси, что вызывает схему излома, представленную на рис. 1.1.
Рис. 1.1. Эпюра напряжений в плоскости, проходящей под углом 450 к продольной оси и перпендикулярной широким граням
- Крутящий момент определяется, исходя из следующих предпосылок:
· от действия крутящего момента излом бетонного элемента происходит по плоскости, проходящей под углом 450 к продольной оси и перпендикулярной к широким граням;
· сечение после деформации остается плоским;
· наибольшее относительное удлинение крайнего растянутого волокна бетона равно 2Rbt /Eb;
· напряжения в бетоне сжатой зоны определяются с учетом упругих деформаций бетона;
· напряжения в бетоне растянутой зоны распределены равномерно и равны Rbt .
Таким образом, это означает, что крутящий момент
вызывает изгибное состояние в плоскости разлома с сечением высотой b
и шириной
![]() .
.
На основе принятых положений и обработки опытных данных получена формула
- Tb = (0,88+0,08h/b)RbtWт,pl , (6)
где Wт,pl - упругопластический момент сопротивления сечения.
Для определения момента трещинообразования железобетонного элемента приемлема формула (6) с той лишь разницей, что в этом случае при определении упругопластического момента сопротивления Wт,pl необходимо учитывать работу арматуры, как и при изгибе.
Для случая изгиба с кручением было установлено, что расчет трещинообразования может быть осуществлен по формулам:
Формулы (7…9) ограничивают область трещинообразования и соответствуют методу графиков взаимодействия.
На основе проведенного анализа имеющихся исследований по рассматриваемому вопросу можно сделать следующие выводы.
1. При анализе научных исследований обнаруживается консерватизм зарубежных исследователей в походе к железобетону в упругой стадии. На основе такого подхода получаются удовлетворительные результаты при рассмотрении опытных данных, полученных при испытании слабоармированных или предварительно напряженных элементов со слабым поперечным армированием, разрушение которых происходит с появлением первой наклонной трещины. Однако, подобный подход к железобетону с нормальным армированием, когда с появлением и развитием трещин образуется блочно-стержневая пространственная структура, нельзя признать удачной и отвечающей фактической работе.
2. Существующие предложения по оценке прочности железобетонных стержней при наличии кручения дают положительную сходимость с опытом для тех образцов, на основе которых эти результаты были получены. При этом такие результаты ограничивались, как правило, одним случаем разрушения - когда образуется пластический шарнир.
3. Расчетный аппарат, полученный на основе ферменной аналогии и принятый ЕКБ-ФИП [3], существенно недооценивает несущую способность элементов, что связано с рядом положений, принятых без достаточного научного обоснования.
4. Метод расчета, принятый СНиП [5], в достаточной мере удовлетворяет оценку прочности в случае разрушения с образованием пластического шарнира при интенсивном изгибе с кручением. При этом четкого разграничения между возможными случаями разрушения с учетом таких важных факторов, как соотношение между силовой интенсивностью поперечного и продольного армирования, а главное между ресурсами прочности бетона на сжатие и арматуры на растяжение, не имеется.
-
- Литература:
1. Касаев Д.Х. Исследование предварительно напряженных элементов, разрушившихся от изгиба с кручением ранее образования пластического шарнира: Дис...канд. техн. наук. - М., 1971. - 117 с.
2. Касаев Д.Х. Прочность элементов железобетонных конструкций при кручении и изгибе с кручением. Ростов н/Д.: Изд-во Рост. ун-та, 2001.-176с.
3. Кодекс-образец ЕКБ-ФИП. - М., 1984. - 284 с.
4. Лессиг Н.Н. Определение несущей способности железобетонных элементов прямоугольного сечения, работающих на изгиб с кручением //Сб. тр. НИИЖБ, М., - 1959. Вып. 5. Исследование прочности элементов железобетонных конструкций. - С.3-28.
5. СНиП 2.03.01-84* Бетонные и железобетонные конструкции. Нормы проектирования. - М.: Стройиздат. 1989. - 79 с.
6. Bach C., Graf O. Versuche uber die Widerstandsfahigkcit von Beton und Eisenbeton gegen Verdrehung //Deutscher Ausschuss fur Eisenbeton, 1912, Heft, N.16. - P - 78.