В работе осуществлен анализ способов измерения площади поверхности различных фигур. Представлен авторский метод расчета площади поверхности фигуры как площади поверхности вращения с предварительным аналитическим описанием контура фигуры.
Ключевые слова:площадь поверхности вращения, интегралы, тела сложной формы.
Для решения определённого рода задач гальваники и металлообработки требуется знать площадь поверхности тела, с которым придётся работать. Однако, не всегда получается быстро осуществить вычисления, ввиду того что некоторые детали имеют нетипичную, сложную форму. Поэтому возникает необходимость найти максимально простой, удобный и экономически выгодный способ для определения этой площади.
Существуют различные подходы к решению данной проблемы. Например, Яскеляин Б. В. и Череднеченко Т. Ф. предложили способ измерения площади поверхности тела, при котором на тело наносят плёнку из материала постоянной толщины, обладающего свойством гигроскопичности, предварительно покрывая поверхность смачивающим составом. Площадь поверхности при этом находят из её геометрической площади с учётом отношения приращения длины плёнки к геометрической длине поверхности [1].
Другой способ был предложен В. Г. Вохмяниным [2]. Он заключался в измерении веса двух тел, простого эталонного (образцового) и измеряемого (сложной формы). Сначала в обычных условиях измеряли вес тел, а затем их охлаждали до температуры конденсации воды и снова проводили взвешивание. Площадь вычисляли, находя частное от деления изменения веса измеряемого тела на изменение веса эталонного. При этом полученное число — это площадь поверхности, выраженная в единицах эталонного тела. Данный способ по сравнению с аналогичными отличается высокой производительностью, простотой, низкой стоимостью и высокой точностью.
Способ измерения площади поверхности, предложенный В. С. Аксельродом и Г. М. Рохлиной [3] позволяет измерить площадь плоской детали сложной формы и основывается на измерении емкости конденсатора. Площадь изделия равна произведению отношения емкости конденсаторов, одной из обкладок которых является измеряемое изделие или эталонное изделие.
Е. Д. Гражданников предложил способ определения величины поверхности твёрдых тел, основанный на измерении сокращения времён спин-решёточной и спин-спиновой магнитной релаксации ядер в слое жидкости, покрывающей поверхность твёрдой фазы [4]. Данный способ предназначен для определения поверхности широкого круга нанесённых веществ и носителей, причём измерения могут быть проведены непосредственно в процессе реакции. Для определения по этому способу площади поверхности нужен эталон изделия, площадь поверхности которого можно измерить другим способом.
Б. Д. Разуваева и К. С. Лыткин, исследуя методы определения площади поверхности сложных изделий, пришли к выводу о том, что метод растворения достаточно надёжен в измерении площади поверхности детали [5]. Он основан на том, что количество металла, растворяющегося в жидкости за единицу времени пропорционально величине поверхности металла. Для определения по этому способу площади поверхности требуется эталонное изделие с известной площадью поверхности.
Каждый из представленных способов предполагает осуществление определенных химические операции с изделием, а также зачастую наличие эталонного тела. В то же время, обратившись к математическому инструментарию, можно осуществить расчет площади поверхности тела аналитически с меньшими затратами.
Например, если изделие обладает центральной симметрией, то его можно рассматривать, как тело вращения. Тогда площадь его поверхности можно рассчитать, как площадь поверхности вращения по формуле:
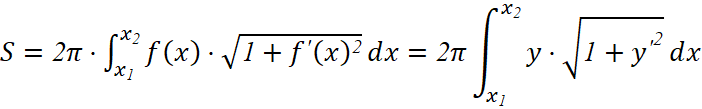 ,
,
где ![]() — аналитическая функция, описывающая контур изделия,
— аналитическая функция, описывающая контур изделия,
x1 и x2 — границы, в которых задана функция.
Рассмотрим более подробное применение данного способа на частном примере. Определим площадь поверхности шахматной пешки (рис.1.).
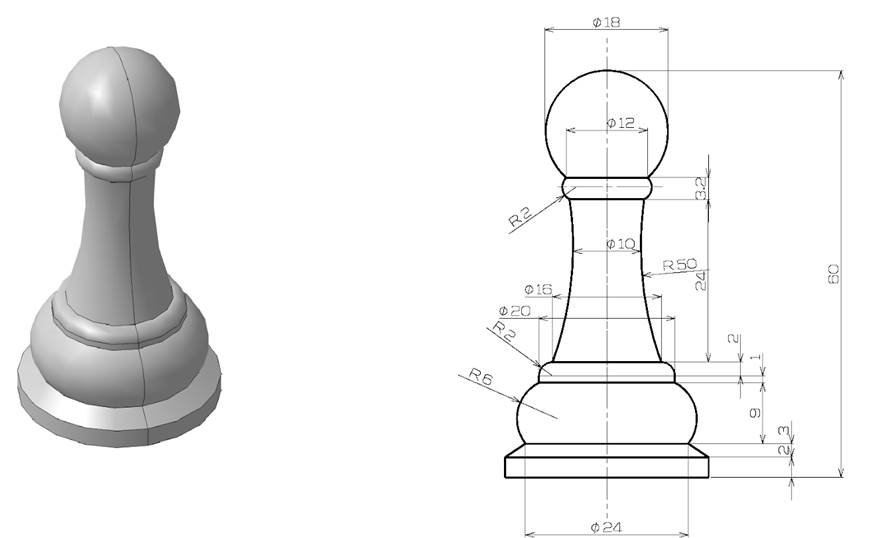
Рис. 1. Шахматная пешка
Поместим контур исследуемого тела в декартову систему координат XOY (рис.2.).
Разные участки контура можно задать различными функциями вида ![]() . Так можно выделить 8 таких функций, задающих контур боковой поверхности, для 8 участков. Так как ищем площадь боковой поверхности, то площадь основания фигуры не рассматриваем.
. Так можно выделить 8 таких функций, задающих контур боковой поверхности, для 8 участков. Так как ищем площадь боковой поверхности, то площадь основания фигуры не рассматриваем.
1) При ![]() — функция —
— функция — ![]()
2) При ![]() — функция —
— функция — ![]()
3) При ![]() — функция —
— функция — ![]()
4) При ![]() — функция —
— функция — ![]()
5) При ![]() — функция —
— функция — ![]()
6) При ![]() — функция —
— функция — ![]()
7) При ![]() — функция —
— функция — ![]()
8) При ![]() — функция —
— функция — ![]()
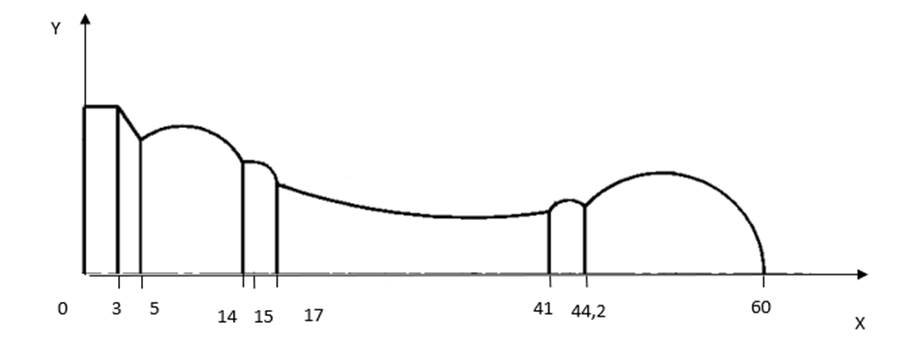
Рис. 2. Контур пешки в системе координат
Найдя данные функции, можно вычислить площадь поверхности этих участков. В ситуациях, когда функция имеет вид ![]() , площадь поверхности участка будет вычисляться также как площадь поверхности цилиндра, по формуле
, площадь поверхности участка будет вычисляться также как площадь поверхности цилиндра, по формуле ![]() , но в данном случае —
, но в данном случае — ![]() , а
, а ![]() , где
, где ![]() и
и ![]() — координаты
— координаты ![]() начала и конца участка соответственно.
начала и конца участка соответственно.
Так, для первого и четвёртого участков площадь поверхности равна соответственно: ![]() ,
, ![]() .
.
Для других участков будет использоваться формула вычисления площади поверхности вращения вдоль оси OX.
Так вычисляем площадь поверхности второго участка:
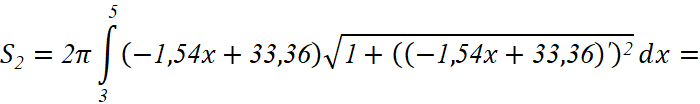
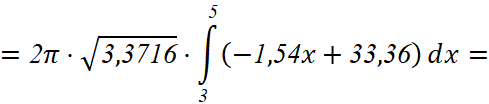
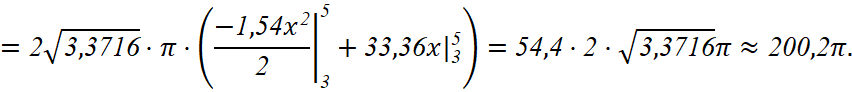
Далее, аналогично, получаем значения площади поверхности остальных участков:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Конечную площадь поверхности находим как сумму площадей поверхностей участков:
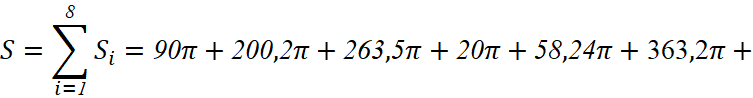
![]() .
.
Данный способ может быть использован для определения площади поверхности тел наряду с ранее упомянутыми. Он будет особенно удобен в случае, если изделие имеет центральную симметрию. Метод отличается точностью и экономической выгодой.
Литература:
1. Яскеляин Б. В., Чередненко Т. Ф. Способ измерения площади поверхности тела сложной формы [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://rusneb.ru/catalog/000224_000128_0093005691_19950720_A_RU/ (дата обращения 22.02.2022)
2. Вохмянин В. Г. Способ В. Г. Вохмянина измерения площади поверхности тела сложной формы [Электронный ресурс] // FREEPATENT: патентный поиск в РФ — URL: https://www.freepatent.ru/patents/2040776 (дата обращения 22.02.2022)
3. Аксельрод В. С., Рохлина Г. М. Способ определения площади поверхности электропроводящих изделий [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000273447_19700615_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
4. Гражданников Е. Д. Способ определения величины поверхности твёрдых тел [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000176457_19651102_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
5. Разуваева Б. Д., Лыткин К. С. Экспресс-метод измерения криволинейных и фактурных поверхностей [Электронный ресурс] // Драгоценные материалы — URL: http://jewelpreciousmetal.ru/technology_other_surfacearea.php ((дата обращения 22.02.2022)







