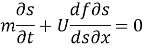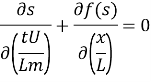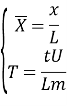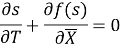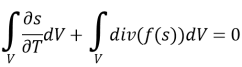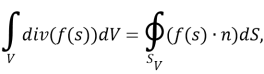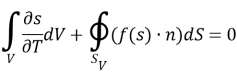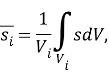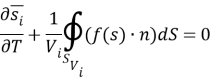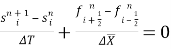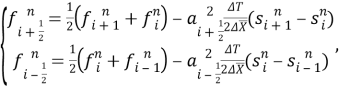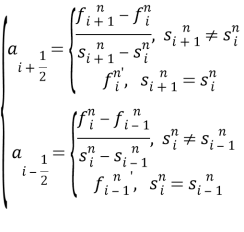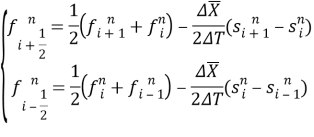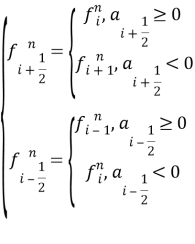Анализ методов решения уравнения Баклея — Леверетта



В статье выполнено сравнение методов Лакса — Вендрофа, Лакса — Фридрихса и Противопоточного методарешения уравнения Баклея — Леверетта.

Ключевые слова: Баклей — Леверетт, гидродинамика, потоки.

Рассмотрим уравнение Баклея — Леверетта для одномерного случая, в котором фильтрация происходит лишь в одном направлении:

(1)

Рассмотрим численные методы решения уравнения Баклея — Леверетта. Для простоты обезразмерим уравнение (1). Для этого поделим обе его части на U/L :

(2)

где L – характерный размер задачи.

Введем следующие обозначения:

(3)

Тогда (2) перепишется в виде:

(4)

Соотношение (4) представляет собой гиперболическое нелинейное уравнение в частных производных.

Для решения (4) воспользуемся методом конечных объемов, который заключается в замене рассматриваемой области расчетной сеткой. Другими словами, осуществляется переход от непрерывного распределения аргумента к его дискретному набору. Метод конечных объемов предполагает, что любые дифференциальные уравнения математической физики получены из интегральных законов сохранения. Таким образом, проинтегрировав (4), перепишем его в следующем виде:

(5)

Используя теорему Остроградского — Гаусса для второго слагаемого, получим:

(6)

где S _V — поверхность рассматриваемого объема V ,

n — единичный внешний вектор, направленный по нормали к поверхности S _V .

Используя полученный результат (6), преобразуем (5) к виду:

((7)

Физический смысл (7) заключается в том, что поток через поверхность, ограничивающую некий объем, равен скорости изменения водонасыщенности в этом объеме.

Введем следующую величину:

(8)

где – среднее значение водонасыщенности в i -ой ячейке рассматриваемой области.

Используя (8), запишем закон сохранения для ячеек по отдельности:

(9)

В данном разделе рассматривается уравнение Баклея — Леверетта для одномерного случая. Тогда вместо ячеек будут использоваться узлы. Также можно полагать, что поток через поверхность ячеек равен потоку от соседних узлов. Расчетная сетка для уравнения (5) имеет вид, представленный на рис. 1.

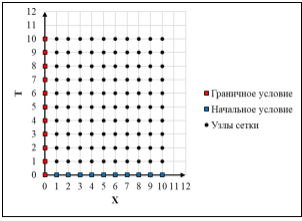
Рис. 1. Расчетная сетка для решения уравнения Баклея — Леверетта

Учитывая вышесказанное, уравнение (5) примет вид:

,

((10)

где – поток водонасыщенности от правого узла,

– поток водонасыщенности от левого узла.

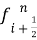
Для определения потоков существует множество методов. В данном разделе будет рассмотрено три метода, так как они обладают различными особенностями, которые нужно учитывать при их применении.

1. Метод Лакса — Вендрофа [2]:

(11)

где

(12)

Используя данный метод, можно получить решение, изображенное на рис 2.

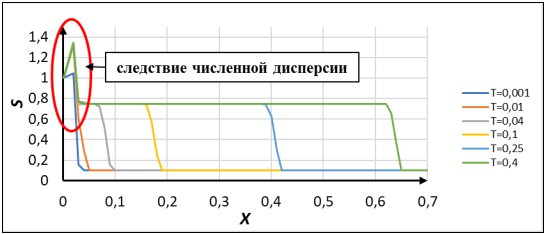
Рис. 2. Решение задачи Баклея — Леверетта методом Лакса — Вендрофа

Как видно из рисунка, применение этого метода влечет за собой появление численной дисперсии в результатах расчета, поэтому использование данного метода не рекомендуется.

3. Метод Лакса — Фридрихса [3]

(13)

Решение данным методом представлено на рис. 3.

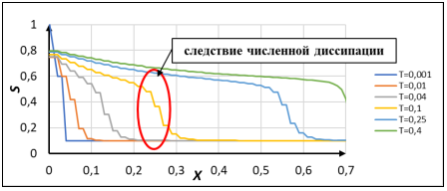
Рис. 3. Решение задачи Баклея — Леверетта методом Лакса — Фридрихса

Результаты, полученные данным методом, обладают значительной численной диссипацией, из-за чего происходит «размытие» скачка обводненности. В настоящей модели этого быть не должно (так как было решено пренебречь капиллярными эффектами, создающими разницу между парциальными давлениями рассматриваемых фаз). То есть использовать данный метод для решения поставленной задачи нецелесообразно.

4. Противопоточный метод upwind [4]

(14)

Результат использования противопоточного метода представлен на рис. 4.

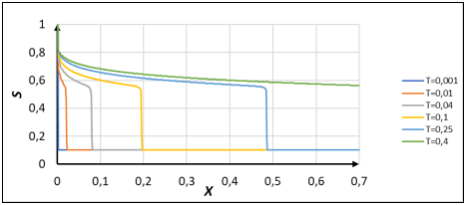
Рис. 4. Решение задачи Баклея — Леверетта противопоточным методом

Видно, что применение последнего метода хорошо описывает решение со скачком водонасыщенности. Полученные результаты не обладают значительной степенью дисперсии и диссипации. Поэтому из всех рассмотренных методов аппроксимации потоков водонасыщенности, использование противопоточного является предпочтительным.

Литература:

1. Ковеня В. М., Чирков Д. В. Методы конечных разностей и конечных объемов для решения задач математической физики. Новосибирск: Издательство Новосибирского государственного университета, 2013. 86 с.
2. Лаевский Ю. М., Кандрюхова Т. А. Об аппроксимации разрывных решений уравнения Баклея — Леверетта // Сибирский журнал вычислительной математики. 2012. Т. 15. № 3. С. 271–280.
3. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Москва: Мир, 1990. 384 с.
4. Губкин А. С. Методические рекомендации к численному решению модельных уравнений математической физики. Тюмень: Тюменский государственный университет, 2018. 11 с.