Решение физических графических задач по кинематике в 9-м классе с использованием языка программирования Python



В статье автор предлагает решать физические задачи по кинематике в 9-м классе с помощью программирования их на языке Python

Ключевые слова: физика, программирование, Python, кинематика.

Двадцать первый век — век высоких технологий. Большинство жителей Российской Федерации имеют персональный компьютер или ноутбук [1]. Школьники с особым интересом играют в компьютерные игры, проходят уровни, забывая для чего изначально был изобретен компьютер — для вычислений. В 9 классе, а многие и в 8 классе, учащиеся по программам курса школьной информатики проходят такой раздел этой науки как программирование, изучая такие языки программирования как PascalABC, Basic, C++ или Python. К сожалению, в школьном курсе физики, имея уже в своем общем разделе — численные методы, никак не используют знания учащимися программирования [2]. В рамках данной статьи автор предлагает использовать язык Python для решения графических кинематических задач в 9 классе по физике.

Итак, перейдем к задаче, которую предстоит решить в рамках настоящей статьи: «Материальная точка движется вдоль оси ОХ по закону: х = 3t. Чему равна скорость материальной точки? Какой путь она пройдет за З с движения?

Постройте график зависимости: а) координаты от времени; б) скорости от времени» [3]

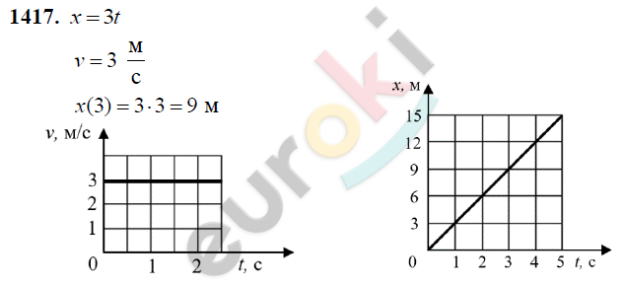
Рис. 1. Стандартное аналитическое решение задачи № 1417 из задачника А. В. Перышкина

На рисунке 1 показано аналитическое решение данной задачи, как она должна быть оформлена и решена в тетради на школьном уроке. Чтобы ее запрограммировать на языке Python учителю требуется рассказать учащимся о библиотеке matplotlib, однако, чтобы не затруднять ученикам жизнь, педагогу важно показать только нужные функции.

Итак, для начала разберемся, что же это за библиотека. Matplotlib — библиотека языка Python, которая помогает визуализировать данные в 2(3)D [4]. Ее используют физики и математики, чтобы вывести графики, анализировать данные, решать задачи. Данная библиотека довольно широкая по своих данным, включая в себя огромное множество функций и технологий, которые на практике в рамках прикладных школьных общеобразовательных базовых задач вовсе не нужны. Ниже приведены функции, которые должен рассказать учитель физики на своих занятиях. Предполагается, что по школьной программе курса информатики учащиеся уже прошли основы программирования.

import matplotlib . pyplot as plt — подключение библиотеки matplotlib к программе. Важно, чтобы данная строчка была написана в самом начале программы.

plt . plot ( y , x ) — подготовка графика к выводу. В качестве аргументов мы указываем x, и y. Стоит заметить, что в отличие от математики, где точка пишется в порядке (x, y), здесь, чтобы вывести правильно оси, нужно писать в порядке (y, x). Важно: x и y — это массивы данных, а не переменные.

plt . show () — вывод графика.

plt . grid () — клетчатая сетка.

plt . xlabel (‘’) — название оси ОХ.

plt . ylabel (‘’) — название оси ОY.

plt . title (‘’) — название графика.

Важно! В функциях, где нужно указывать названия, по обе стороны от текста по правилам типизации данных языка Python, ставятся одинарные кавычки.

Итак, перейдем к программированию задачи (см. лизинг 1). Наша задача найти, чему будет равна скорость, путь и вывести два графика — зависимость скорости от времени и зависимость координаты от времени.

Листинг 1. Решение первой задачи

1. import matplotlib.pyplot as plt
2. v, x, t = [], [], []
3. for i in range(1, 6):
4. xt = 3*i
5. v2 = xt/i
6. v.append(v2)
7. t.append(i)
8. x.append(xt)
9. print('Скорость равна: ', v2, 'м/c')
10. print('Расстояние равно: ', v2*3,'м')
11. plt.grid()
12. plt.title('График зависимости координаты от времени')
13. plt.xlabel('t, с')
14. plt.ylabel('x, м')
15. plt.plot(t, x)
16. plt.show()
17. plt.grid()
18. plt.title('График зависимости скорости от времени')
19. plt.xlabel('t, с')
20. plt.ylabel('v, м/c')
21. plt.plot(t, v)
22. plt.show()

Для удобства автор пронумеровал каждую строчку, как в редакторе кода, чтобы в рамках данной работы было легче ссылаться на них.

Так как нам следует выводить графики зависимости скорости от времени и зависимость координаты от времени — создадим массивы v. x и t, как написано в строчке 2, где v — массив скорости, x — массив координат, а t — массив времени. В данном случае они пустые, поэтому внутри квадратных скобок нет элементов.

В третьей строчке мы создаем цикл, который будет заполнять массивы. За переменную i, которая считается счетчиком с шагом один, мы будем принимать время в секундах, а чтобы в пятой строчке не было ошибки деления на ноль, мы начали цикл с цифры 1. Переменная xt из 4 строчки — это закон движения, который дан нам в условии задачи. В 5 строчке переменная v2 — является расчетной для скорости. Каждый проход цикла она изменяется (с точки зрения формулы), так как зависит от изменяемых величин — координаты (переменная xt) и времени (переменная i). В 6 строчке полученная в 5 строчке скорость добавляется в массив v, который в дальнейшем мы будем использовать для вывода графика зависимости скорости от времени, а что касается времени, то в 7 строчке переменная i, каждый проход цикла добавляется в массив t. В 8 строчке таким же образом каждый проход цикла добавляется в массив x координата xt. Итого, у нас заполнено три массива — скорость, время и координата. В 9 строчке выводится значение скорости через переменную v2. Автор не стал изменять переменную скорости для вывода, так как v2 по закону равномерного движения постоянна и не изменяема. В 10 строчке выводится расстояние. Так как расстояние — это скорость, умноженная на время, а в условии задачи сказано найти расстояние, пройденное за 3 секунды, то у нас умножается переменная v2 на 3.

В 11 и 17 строчках мы создаем сетки для графиков зависимостей, указанных в условии задачи. В строчках 12 и 18 — название графиков, а в строчках 13, 14, 19, 20 — название осей. В строчках 15 и 16 у нас проектируется и выводится график зависимости координаты от времени, а в строчках 21 и 22 — зависимости скорости от времени соответственно.

Теперь посмотри на вывод результатов:

Рис. 2. Вывод скорости и расстояния

На рисунке 2 представлены результаты первой части задачи — скорости и расстояния.

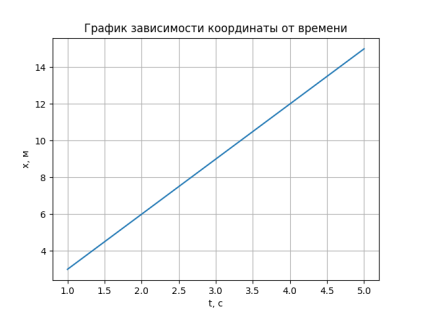
Рис. 3. График зависимости координаты от времени, полученные при запуске задачи

На рисунке 3 показан график зависимости координаты от времени, который вывелся в программе, как результат обработки алгоритма. Как мы видим, он совпадает с тем, что получился при аналитическом решении. Теперь выведем следующий график:

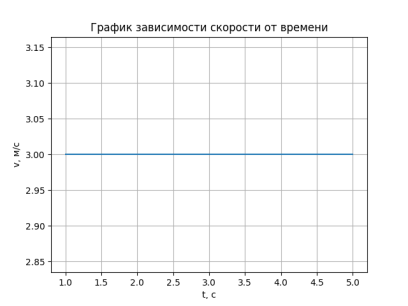
Рис. 4. График зависимости скорости от времени

На рисунке 4 показан график зависимости скорости от времени, который также совпадает с аналитическим решением. В школе на уроке учителю можно рассказывать аналитический способ, а на элективных уроках (внеурочной деятельности), на основе решения в классе, решать и обсуждать численные методы решения подобных задач.

Численных методов не хватает в школьной программе, поэтому автор предлагает решать задачи таким образом, используя язык программирования Python как основной инструмент. Таким образом можно решать любые задачи по физике, где требуются графики, будь это задачи по динамике на нахождение зависимости сил от какой-либо величины, так и задачи на электростатику, где нужно построить график зависимости силы Кулона от расстояния между зарядами, которые удаляются друг от друга.

Литература:

1. ВЦИОМ: только у 22 % россиян нет компьютера или ноутбука Источник: https://realnoevremya.ru/news/183033-vciom-tolko-u-22-rossiyan-net-kompyutera-ili-noutbuka. — Текст: электронный // https://realnoevremya.ru/news/183033-vciom-tolko-u-22-rossiyan-net-kompyutera-ili-noutbuka: [сайт]. — URL: https://realnoevremya.ru/news/183033-vciom-tolko-u-22-rossiyan-net-kompyutera-ili-noutbuka (дата обращения: 27.04.2022).
2. Сахтарек, И. Ч. Календарно-тематическое планирование по физике 9 класс / И. Ч. Сахтарек. — Текст: электронный // https://nsportal.ru/shkola/fizika/library/2015/12/18/kalendarno-tematicheskoe-planirovanie-po-fizike-9-klass: [сайт]. — URL: https://nsportal.ru/shkola/fizika/library/2015/12/18/kalendarno-tematicheskoe-planirovanie-po-fizike-9-klass (дата обращения: 27.04.2022).
3. Перышкин, А. В. Сборник задач по физике / А. В. Перышкин. — 19-е изд. — Москва: Экзамен, 2017. — 271 c. — Текст: непосредственный.
4. Matplotlib 3.5.1 documentation. — Текст: электронный // https://matplotlib.org/stable/index.html: [сайт]. — URL: https://matplotlib.org/stable/tutorials/introductory/usage.html (дата обращения: 27.04.2022).