This article has developed a mathematical model of energy processes of Earthquakes of South Kyrgyzstan. Here, an end-to-its-characterized regulatory solution to a one-dimensional reverse problem of seismic was built here.
The author revealed, from the point of view of the practical task of seismic, the best method is the end-and-playing method, which needs to establish the stability of the solution.
Keywords: the natural phenomenon, earthquake, seismic equations, energy process, of course, regulatory solution, Aikonal method, task, method of highlighting features,inverse task.
Introduction. Earthquake. It is known that an earthquake is tectonic deformations of the earth's crust, due to accumulating stress, which come to the surface of the earth in the form of shocks in different power [2]. With each earthquake in the bowels of the Earth, a certain amount of energy is released, which accumulated constantly and continuously. To identify, recognize natural phenomena preceding earthquakes, monitoring (constant tracking) is carried out behind the time (or invariable) physical conditions in the area under consideration, the characteristics of the waves and deformation of the rocks.
To achieve such goals, it is necessary to develop new effective methods of mathematical modeling [8].
1. Formulation of the task. For the seismic equation, consider the reverse task:
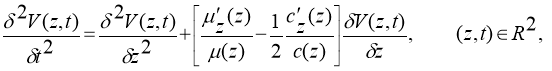
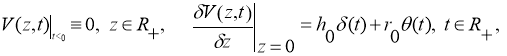
where —
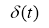
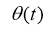
Let the solution of the direct task be given, to solve the inverse task,
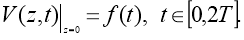
Let the conditions be met with respect to the coefficients of the equation
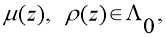
where
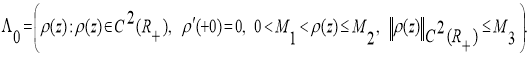
Equation (1) is an equation of hyperbolic type, so the task can be considered in the field of ∆(Т) [1]:
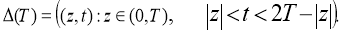
The inverse task
is to determine
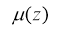
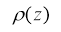
Let's denote by
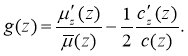
The singular and regular part of the solution of the direct decision (1) -(2) will be allocated according to the method of V. G. Romanov (the method of allocating features) for this purpose we present the solution of the problem in the form of [1]:
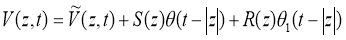
where
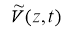
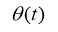
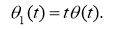
The last calculations are substituted into equation (1), and we get
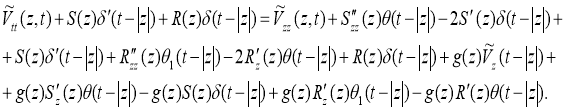
Collect the members at the same coefficients
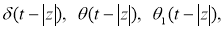
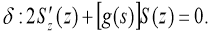
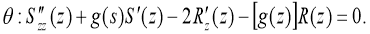
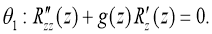
Then we will
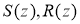
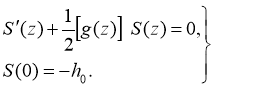
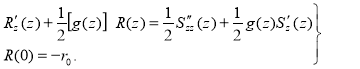
To
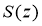
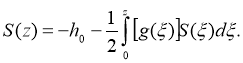
To
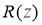
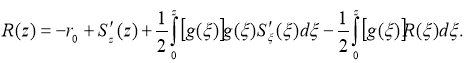
If we consider that
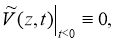
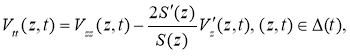
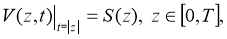
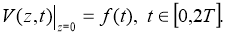
The inverse problem (13)
— (15) is to define
afunction,
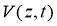
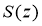
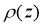
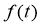
If we define functions
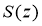
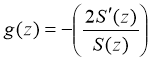
we can also define an unknown function
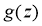
Using the D'Alembert formula for a direct task (13), (14), we get a solution to a direct problem [7]:
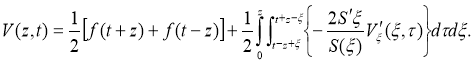
With (17)
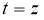
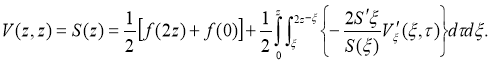
2. Let's build a finite difference solution. Let's introduce a grid area for solving problem (13)-(15):
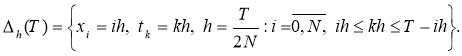
where
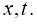
The difference analogue of the differential equation (13) will be:
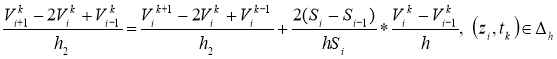
From (19) we get
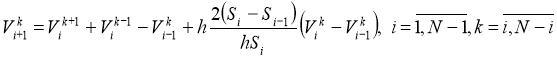
From the last expressions we can get the recurrence formula [3]:
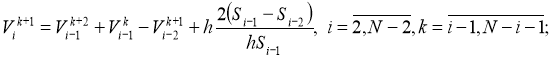
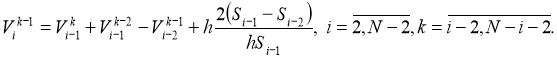
The last expressions are substituted sequentially in the right part (21), and also again writing the same recurrent formula and supplying it to (21) and continuing this process we get a difference analogue of the integral formula of Alembert(17):
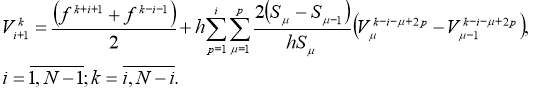
Suppose that in the last formula (22)
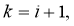
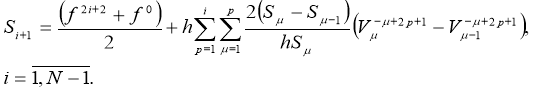
The difference formulas (22) and (23) constitute a system of difference nonlinear equations of the second kind.
In the difference analogue (22) we wrote without small quantities
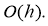
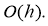
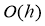
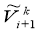
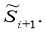
Then for
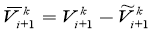
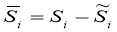
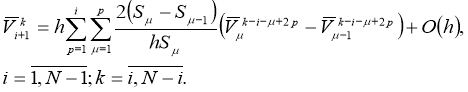
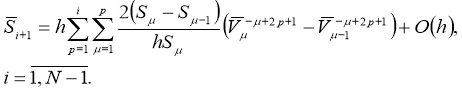
Let's introduce notation
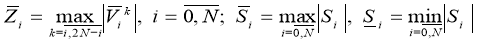
Given these designations from (24) and (25) we will get estimates
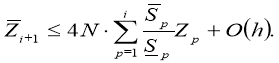
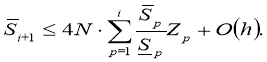
Let
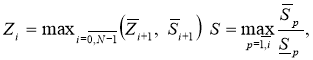
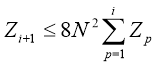
From the last formula, using a discrete analogue of Gronulla-Bellman, we get
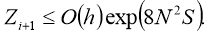
The following theorem on the convergence of the finite-difference solution of the difference task (22), (23) to the solution of the differential decision (13) — (15) is proved.
Theorem 1.
Let the solution of the differential task(14) (15) exist
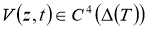
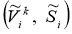
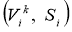
Build a
finite-difference regularized solution.
Let the additional information about solving the direct decision, for solving the inverse task, be given in the form
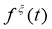
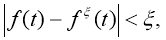
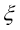
Then for
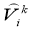
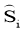
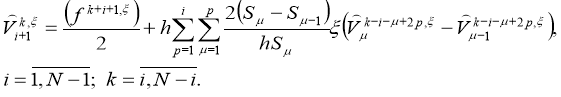
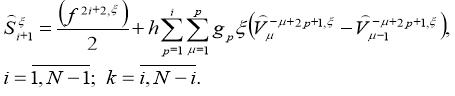
Taking into account the introduced norms, we will evaluate the latest equations
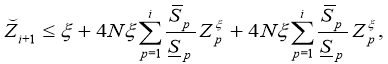
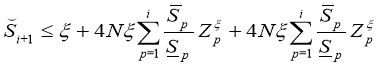
Let
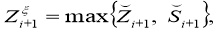
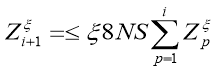
Then again using the Gronole–Bellman formulas, we get an estimate
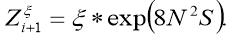
And if we consider that the ratings (30), we have
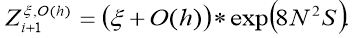
The last estimate is an estimate of the regularized solution of the inverse task.
Theorem 2.
Let the solution of the direct task(13)-(15) exist and let
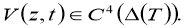
Of course, the difference regularized solution of the original inverse problem (1) — (3) is obtained from formula (16):
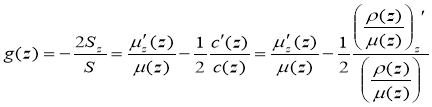
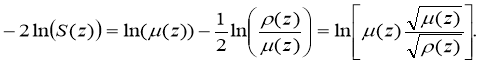
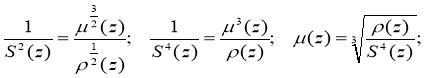
Thus, the finite-difference regularized solution of the inverse problem (1) — (3) has the form:
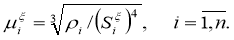
References:
- Satybaev A.Dj. Finite-difference regularized solution of inverse problems of hyperbolic type. Osh. Oshobltypography. 2001. 143 p.
- Satybaev A.Dj., Alimkanov A. A. Numerical method of solving a one-dimensional inverse seismic problem with instantaneous and corded sources. Marchukov scientific works — 2017. June 25 — July 14, 2017. Novosibirsk: IVMiMG SB RAN, 2017. p.776–881.
- Satybaev A.Dj., Alimkanov A. A. Finite-difference determination of the density of the medium in the one-dimensional inverse problem of seismic. Izvestiya KSTU named after I.Razzakov. 2017, No1(41), part I. Tokmok, 2017, p. 113–123.
- Satybaev A.Dj., Alimkanov A. A. Algorithm for determining one inverse seismic problem with instantaneous and corded source. Izvestiya KSTU, No3(39), part I. Bishkek-2016, page 175–180.
- Kabanikhin S. I. Inverse and incorrect tasks. Novosibirsk. Sib. scientific publishing house.2009–457 p.
- Romanov V. G. Stability in inverse problems. M.: Nauchnyi mir. 2005. 296 page.
- Mamatkasimova A. T., Satybaev A. J. Development of a finite-difference regularized solution to a one-dimensional inverse problem arising in electromagnetic processes. Collection of articles on the materials of the XXXVIII International Scientific Practical Conference «Natural and Mathematical Sciences in the Modern World», No. 1 (36), January 2016, Novosibirsk, 2016. page 29–45.
- Nikonov A. A. Earthquake. M.:, Znanie (past, present, forecast) 1984, p.192.
- Alimkanov A. A. Numerical method of solving a one-dimensional inverse seismic problem with instantaneous and corded sources. NEWS OF UNIVERSITIES OF KYRGYZSTAN — Bishkek — 2015. — No. 11, Republican Scientific and Theoretical Journal; pp. 3–7.







