Работа посвящена исследованию одной краевой задачи для параболического уравнения, возникающее при моделировании процесса температурного режима пахотного слоя чернозема выщелоченного. Задача заключается в нахождении температуры из краевой задачи для уравнения теплопроводности со смешанными граничными условиями. Доказывается теорема об однозначной разрешимости рассматриваемой задачи и получено соответствующее явное аналитическое решение.
Ключевые слова: моделирование, температурный режим, чернозем выщелоченный, пахотный слой, температуропроводность, параболическое уравнение, краевая задача.
The work is devoted to the study of one boundary value problem for a parabolic equation that arises when modeling the process of the temperature regime of the arable layer of leached chernozem. The problem is to find the temperature from the boundary value problem for the heat equation with mixed boundary conditions. A theorem on the unique solvability of the problem under consideration is proved and the corresponding explicit analytical solution is obtained.
Keywords: modeling, temperature regime, leached chernozem, arable layer, thermal diffusivity, parabolic equation, boundary value problem.
Температурный режим почвы оказывает существенное влияние на развитие и рост растений. Поэтому задача определения температуры в активном слое почвы является актуальной. Измерение температуры почвы по глубине во времени непосредственно в поле связано с определенными трудностями, а при масштабных исследованиях практически невозможно. Альтернативой экспериментальным методам служат расчетные. В настоящее время в математической физике чаще всего используют аналитические (если это возможно) и численные методы, имеющие ряд преимуществ перед другими.
В данной работе изучается одномерная математическая модель температурного режима почвы, основанная на уравнении теплопроводности с известными начальным и граничным условиями 2-го рода на верхней границе поверхности и условия 1-го рода на нижней границе поверхности, где рассматриваются теплообменные процессы внутри почвенного массива, определяемые его структурными неоднородностями, а термическая ситуация вблизи поверхности почвы рассматривается как фон, на котором указанные процессы изучаются [1]. В работе [2] рассматриваемая нами задача исследована разностным методом и применен для конкретного практического примера.
Постановка задачи и основной результат
Рассматриваемый почвенный массив состоит из одного однородного горизонтального слоя, для которого характерны определенная плотность ρ , теплоемкость с и теплопроводность λ . Для нахождения температурного поля запишем уравнение теплопроводности:
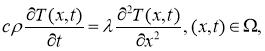
где
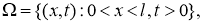
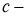
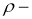
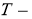
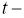
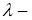
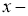
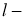
Вводяобозначение
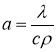
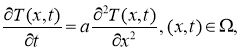
где
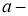
Краевое условие на верхней границе задаем в виде динамики температуры деятельности поверхности [1]:
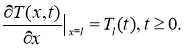
Краевое условие на нижней границе определим нулевым градиентом температуры:
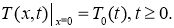
Здесь
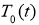
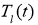
Начальное распределение температуры на почвы в глубине имеет вид
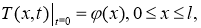
где
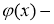
Теорема.
Пусть
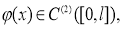
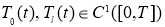
удовлетворяют следующим условиям согласования:
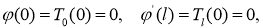
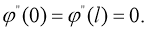
Тогда краевая задача (1) -(3) имеет единственное классическое решение и это решение представимо в виде
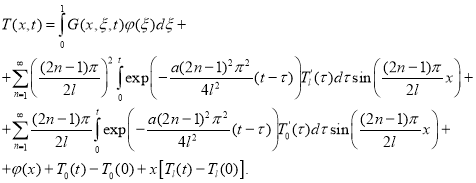
Доказательство. Как и в работе [3, 4], сделав замену
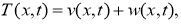
где
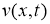
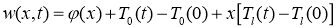
задачу (1) -(3) сведем к задаче
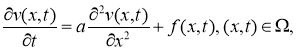
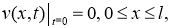
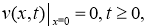
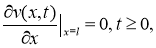
где
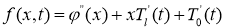
Решение задачи (8) -(11) ищем в виде
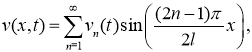
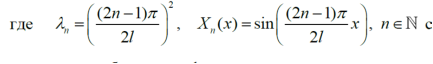
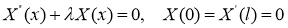
Тогда для определения функции
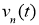
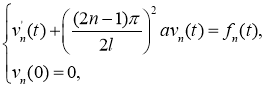
где
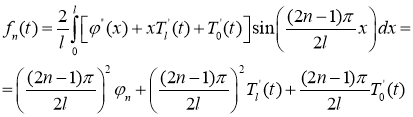
Учитывая (14) решение задачи (13) запишем в виде:
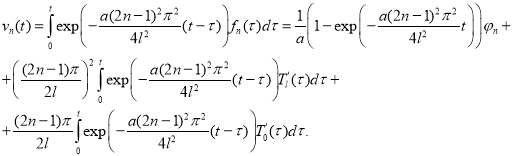
где
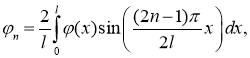
Подставляя (15) в (12), получим явное решение задачи (8) — (11):
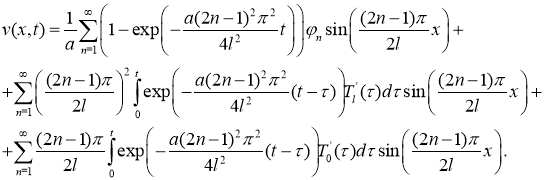
или
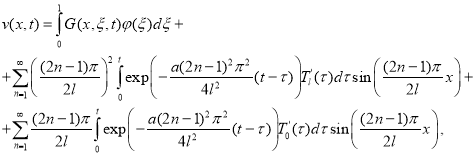
где
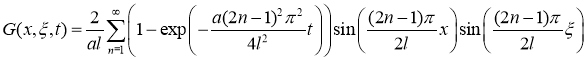
Подставив последную формулу в (7), получим явное решение (6). Теорема доказана.
Вывод
При решении задач для рассмотренной модели получено явное аналитическое решение, которое можно использовать во многих практических случаях.
Литература:
1. Чудновский А. Ф. Теплофизика почвы. -Наука, М., 1976, 352 с.
2. Макарычев С. В., Болотов А. Г., Гефке И. В. Математическое моделирование температурного режима пахотного слоя чернезема выщелоченного // Вестник АГАУ. -2010.-№ 5.- (67).- С.26–28.
3. Аблабеков Б. С. Обратные задачи для псевдопараболических уравнений. — Бишкек: Илим, 2001. –183 с.
4. Аблабеков Б. С., Муканбетова А. Т. О разрешимости решений первой начально-краевой задачи для псевдопараболического уравнения с малым параметром // Евразийское научное объединение. –2019.Т.1. –№ 4(50). –С.1 –5.







