1. Проблема исследования. Большинство учащихся считает, что тригонометрия сложна и абстракта для изучения. При решении задач на раздел «Тригонометрия» у учащихся наблюдаются затруднения и на практике мы выявили основные факторы, которые на это влияют:
— запоминание тригонометрических формул;
— использование тригонометричесих формул;
— незаинтересованность темой, из-за большего количества формул;
— объем содержания и количество часов не соответствуют (по программе обучения на раздел выделяется мало часов).
Проблема нашего иследования заключается в рассмотрении теоретичских основ тригонометрии и методики ее изучения. Из-за того, что материалы программы 9–10 классов являются основой для тем 12 класса, перед учащимися, которые сдают внешнее суммативное оценивание (ВСО), поставили цель развить память и навыки использования тригонометрических формул при решении задач.
2. Планирование. Чтобы внедрить эффективные методы при решении тригонометрических задач, для исследования возникшей проблемы в процессе обучения объединились с учителями преподающие в 9, 10, 12 классов. Для достижения цели на уроках математики использовали такие методы и приемы исследовательской деятельности учащихся: проблемный метод, исследовательский метод и эвристический метод. Все эти навыки помогают учащимся развить критическое мышление, которое необходимо для решения ряда задач по тригонометрии. Данный вид мышления используется как инструмент для принятия точных, обоснованных решений [1]. Исследование началось с нахождение ответа на следующие вопросы:
1) Как улучшить понимание основных тригонометрических концепции с учетом методических особенностей изучения раздела тригонометрии;
2) Как оценить эффективность выбранных методов;
3) Есть ли существенная разница в результатах после проведения исследования;
Чтобы ответить на эти вопросы изучили научно-методическую литературу. На уроках применяли различные подходы при изложении тем.
3. Определение объектов. Основы тригонометрии и основные тригонометрические тождества учащиеся начинают изучать в 8 классе. Далее в 9 классе начинают изучение тригонометрических функций и их свойств. Также в этот период учащиеся изучают тригонометрические формулы. В 10 классе узнают о понятии обратных тригонометрических функций, учатся решать тригонометрические уравнения и неравенства. В 11 классе учащиеся начинают изучать тему “Обратные тригонометрические неравенства” и как мы видим на практике возникают проблемы, т. к. учащиеся не показывают ожидаемых результатов в твердом знаний ранее изученных тем и формул. Каждая новая тема связана с тригонометрическими формулами, и поэтому было проведено наблюдение за учащимися 9, 10, 12 классов.
4. Этапы исследования. Ожидалось, что, использование исследовательских методов обучения помогут улучшить математическое образование. Активные методы и методы запоминания дают учащимся знания о тригонометрии лишь на короткое время, так как полученные знания не сохраняются в памяти учащихся в долгосрочной перспективе. Исследование начали с проведения опроса среду учащихся. Результаты данного опроса показали какие темы самые трудные для понимания и какие тригонометрические задачи вызывают проблемы. Данные помогли сосредоточиться на этих темах тригонометрии, а затем медленно перейти к другим темам. Самыми сложными были такие темы как: “Формулы половинного аргумента”, “Преобразование произведения тригонометрических функций в сумму”, “Формулы понижения степени”, “Тригонометрические неравенства”, “Обратные тригонометрические неравенства”.
5. Результаты. Для сбора данных использовали результаты тестового задания из 20 вопросов после внедрения методов исследовательской деятельности. До исследования учащихся 9 классов не могли воспроизвести формулы самостоятельно, а после исследования результаты теста показали, что половина из них научились не затрудняясь выводить формулы. Также учащиеся 10 и 12 классов во время пробного ВСО добились значительных результатов.
6. Обратная связь учащихся. По окончанию исследования был взят опрос у учащихся, где они оценивали свой прогресс по усвоению раздела тригонометрии на основе проведенного теста из 20 вопросов. В опросе приняли участие 84 учащиеся 9–12 классов. Шкала показывает уровень усвоения учебного материала, где 1 — нет результата, допускаю много ошибок; 2 — частично справляюсь с заданиями; 3 — справляюсь с большинством заданий, но есть затруднения; 4 — допускаю незначительные ошибки в заданиях;
5 — полностью справляюсь с заданиями (Рис.1.).
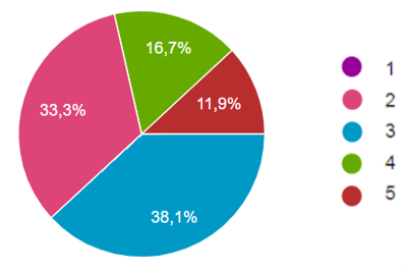
Рис. 1. Диаграмма уровеня усвоения учебного материала учащимися
7. Выводы. Ожидалось, что, использование исследовательских методов обучения помогут улучшить математическое образование. И результаты исследования показывают, что выбранная модель обучения в незначительной степени повысила успеваемость учащихся. Процент выполнения тригонометрических заданий повысился. В дальнейшем на уроках необходимо уделять внимание решению задач как в классе, так и на уроке для предупреждения и устранения ошибок учащихся.
Литература:
- Halpern D F 2002 Thought & Knowledge: An Introduction to Critical Thinking (United States of America: Lawrence Erlbaum Associates) p. 2.
- Engaging problems on trigonometry: why were student hard to think critically? To cite this article: M Aminudin et al 2019 J. Phys.: Conf. Ser. 1188 012038.







