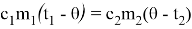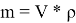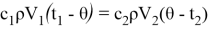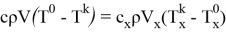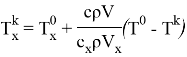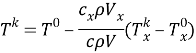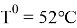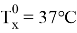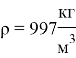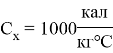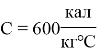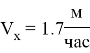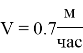Статья описывает процесс передачи теплоты от одного вещества-теплоносителя к другому теплоносителю. Актуальность работы использование математических моделей, численных методов, специализированных пакетов и компьютеров является необходимым условием решения задач моделирования, расчета и проектирования процессов и оборудования биогазовой технологии. От его эффективной работы во многом зависит протекание всего процесса метанового сбраживания и качество получаемого биогаза.
Ключевые слова: теплообменник, математическая модель, температура потоков, трехступенчатая биогазовая установка
The article describes the process of heat transfer from one coolant substance to another coolant. The relevance of the work The use of mathematical models, numerical methods, specialized packages and computers is a necessary condition for solving the problems of modeling, calculating and designing processes and equipment for biogas technology. The flow of the entire process of methane fermentation and the quality of the resulting biogas largely depend on its efficient operation.
Keywords: heat exchanger, mathematical model, flow temperature, three-stage biogas plant
В данной статье рассматриваем: процесс передачи тепла отбираемого потока из биореактора с термофильным температурным режимом потоку поступающему на метановое сбраживания в биореактор мезофильного температурного режима. Далее происходит процесс передачи тепла потоку отбираемому из биореактора с психрофильным температурным режимом, поступающего на сбраживание в биореактор мезофильного температурного режима:
- Передачу теплоты от греющего потока субстрата с температурой 52 градуса к потоку субстрата с температурой 37 градусов
- Передачу теплоты от греющего потока субстрата с температурой 44 градуса к потоку субстрата с температурой 25 градусов
- Гидравлическое сопративление (потерю давления) при прохождении воды по внутренной трубе теплообменника.
- Функциональная схема узлов подготовки сырья и метанового сбраживания в трехступенчатой биогазовой установке приведена на рис. 1 [1].
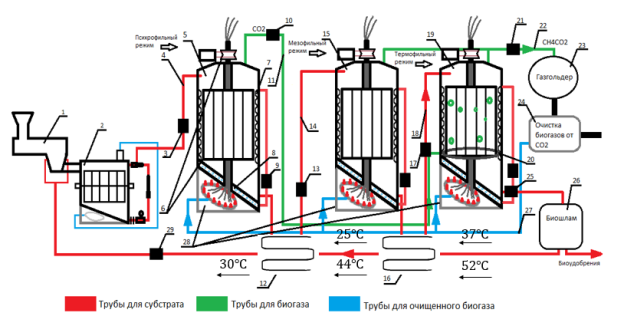
Рис. 1. Функциональная схема узлов подготовки сырья и метанового сбраживания в трехступенчатой биогазовой установке
Процесс метанового сбраживания субстрата в узле происходит в следующем порядке. В биореактор 5 психрофильного режима субстрат заливают ежедневно дозу субстрата 11 дней, в процессе анаэробного сбраживания в 5 биогаз обогащенный С0 2 насосом 10 подается на барботаж в биореактор — термофильный режим 19. При поступлении 12 дозы, из нижней части отбирается одна доза и проходит теплообменник 12 и с помощью насоса 13 подаётся в биореактор — мезофильного режима 15 на сбраживание.
Процесс подачи доз ежедневно продлится до 9 раз, при этом получаемый биогаз отбирается через компрессор 21 в газгольдер 23. После 20 суток перекачивающий насос 17 отбирает одну дозу, которая проходит теплообменник 16 и подается в биореактор 19. Процесс подачи доз ежедневно продлится до 8 раз. Выделяемый биогаз с помощью компрессора 21 откачивается в газгольдер 23 и после очистки 24 отправляется к потребителю биогаза 27 и на отопление биореакторов 5,15,19 [2, 3].
Математическая модель
Поскольку теплообменник прямоточный, математическая модель задается следующей системой уравнений [4]:
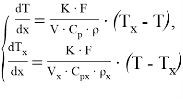
где:
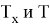
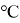
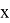
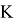
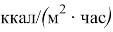
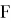
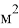
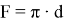
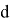
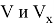
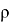
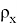
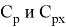
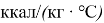
Для реализации математической модели теплообменника для противотока используем VisualStudio, программный код напишем на языке С++. Графики результатов получаем на Excel.
В режимах противотока для систем дифференциальных уравнений, соответствующие краевые условии:
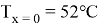
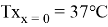
Для решения систему математического моделя теплообменника используем итерационный метод Эйлера.
Аппроксимация дифференцияльного уравнения для горячего потока:
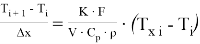
Рекуррентная формула:
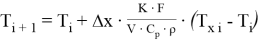
Аппроксимация дифференцияльного уравнения для холодного потока:
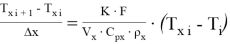
Рекуррентная формула:
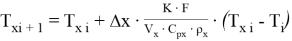
Аналитическое решение
Для аналитического решения мы принимаем уравнения (1) теплового баланса [6]:
|
|
(1) |
|
где
|
(2) |
подставляя (2) — уравнения на (1) получаем следующее уравнение:
|
|
(3) |
Плотность оба потока будет равными. Подстраиваем переменные на нашу задачу:
|
|
(4) |
Где
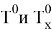
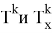
От (4) — уравнения выразим формулу рассчета конечной температуры холодного потока:
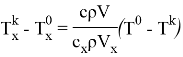
|
|
(5) |
Аналогично получаем формулу рассчета конечной температуры горячего потока [7, 8]:
|
|
(6) |
Исходные данные:
|
|
Начальная температура горячего потока |
|
|
Начальная температура холодного потока |
|
|
Плотность воды (плотность потоков) |
|
|
Теплоемкость холодного потока |
|
|
Теплоемкость горячего потока |
|
|
Скорость холодного потока |
|
|
Скорость горячего потока |
Расчетные данные:
Подставляя исходные данные на (5) — уравнение мы получаем:
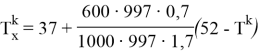
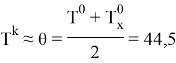
Где
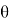
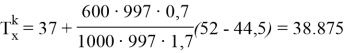
После нахождения конечных температур потоков, используя (7) –уравнения мы можем подсчитать расход передаваемой теплоты:
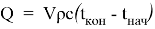
Расход передаваемой теплоты холодного потока:
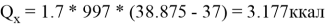
Расход передаваемой теплоты горячего потока:
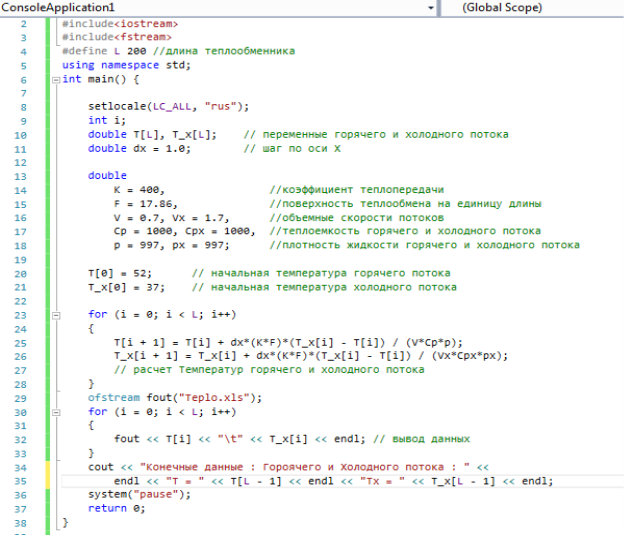
Реализация математической модели консоли Visualstudio на языке С++
Листинг программного кода
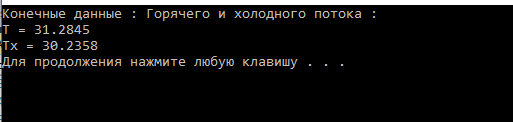
Результат расчета первого теплообменника температуры потоков по математической модели [9]:

Полученные результаты отображены на графике при изменении температур:
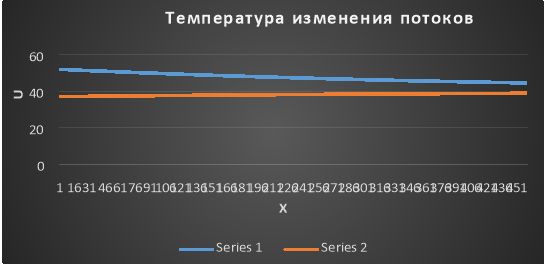
Результат расчета второго теплообменника температуры потоков по математической модели:
Полученные результаты отображены на графике при изменении температур:
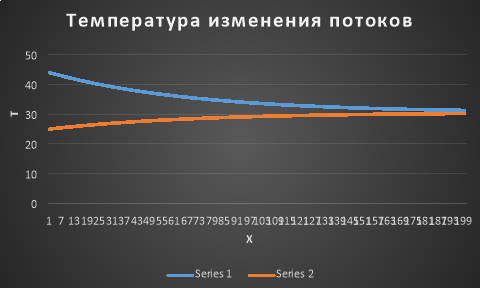
Таким образом, оборотный поток с биореактора термофильного температурного режима поступает в первый теплообменник с температурой 52
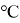
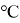
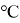
Прямой же поток измельченного субстрата с температурой 25
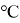
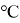
Отбираемый же поток поступает в первый теплообменник и нагревается до 38
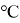
Если посмотреть на полученные результаты, то получается, что тепло обменивается в достаточном количестве, исходя из графиков, расчет ведется правильно, мы видим, что под воздействием поступающей тепловой воды воздух прогревается и вне трубы, т. е. процесс теплообмена идет правильно. В дальнейшем данная модель может быть применена к теплообменникам различного назначения.
Литература:
- Baijarikova, M. A. Mathematical Research of the Accelerated Three-Stage Process of Substrate Fermentation in Bioreactors [Текст] / [Baijarikova M. A., TlebayevM.B., TazhiyevaR.N.и.др.]. Journal of Phfrmaceutical Sciencesand ResearchVol. 9(4), 2017, -C 392–400.
- Байжарикова, М.А. «Способ переработки органических отходов» [Текст]/ [Байжарикова М. А., Тлебаев М. Б., Тажиева Р. Н.и. др.]. Патент № 103153.-Казахстан. 2016.
- Добышев, А. С. Подбор и подготовка животноводческого сырья для биогазовых установок. [Текст] /Добышев А. С., Острейко А. А. УО «Белорусская государственная сельскохозяйственная академия» г. Горки, С, 394–401.
- Приходько Р. А., Растеряев Н. В., Моделирование температурного поля теплообменника «труба в трубе»
- С. Г. Ефимова, В. Т. Чупров Теплотехника
- В. В. Филиппов, Теплообмен в химической технологии
- Н. Ю. Карапузова, В. М. Фокин, Расчет теплообменных аппаратов
- А. Л. Проскурнин, Исследование процесса теплообмена в теплообменнике типа «труба в трубе»
- А. В. Могилев, Пак Н. И., Хённер Е. К., Информатика.