Для изучения процесса трещинообразования в балках с помощью численного моделирования нужно иметь модель, которая бы корректно отражала работу конструкции под нагрузкой. Таки образом, была поставлена задача по созданию такой модели.
В статье приводится описание процесса моделирования железобетонной балки, усиленной внешним ФАП-армированием в программе Abaqus. Для оценки корректности работы модели, сопоставляется характер распределения трещин с балкой, испытанной в лабораторных условиях. Сравнивается картина трещинообразования в балке с внешнем армированием и без него.
Ключевые слова: моделирование, Abaqus, ФАП-ламинат, железобетонная балка, трещинообразование.
Введение
Применение фиброармированных полимеров (далее — ФАП) для усиления железобетонных конструкций находит широкое применение в строительстве. Это связано с их превосходными свойствами, такими как легкий вес, высокая прочность на растяжение и коррозионная стойкость. При этом, использование системы внешнего армирования, подразумевает под собой и более сложный характер работы под нагрузкой в целом всей конструкции.
Возможны различные сценарии разрушение усиленных балок: в результате разрыва ФАП, разрушения бетона, отслоение ламината у его концов от развития наклонных трещин и последующего дробления бетона в уровне защитного слоя, отслоение ламината в середине пролета от развития нормальной трещины и прочие [1]. Понять причины, по которым разрушение пошло по тому или иному сценарию, определить факторы, которые в большей или в меньшей степени повлияли на это — вот, что поможет спроектировать конструкцию, которая будет работать максимально эффективно.
Одним из главных путей к получению информации, позволяющей достичь вышесказанного, является проведение экспериментов, в том числе и численных с применением программ, таких как ABAQUS — многоцелевого конечно-элементного комплекса для инженерного анализа.
В данной работе ставится цель создать достаточно простую рабочую модель, которая бы позволяла проследить процесс развития трещин в балках с внешним армированием ФАП-ламинатом.
Расчетная схема балки
Для того, что можно было оценить корректность результатов численного исследования, моделируется балка, ранее испытываемая в лабораторных условиях [1]. Расчетная схема балки приведена на (рис. 1).
![Расчетная схема балки, испытываемой в [1]](https://moluch.ru/blmcbn/91846/91846.001.png)
Рис. 1. Расчетная схема балки, испытываемой в [1]
Механические свойства материалов, которые применялись в исследовании [1] представлены в табл. 1.
Таблица 1
Механические свойства материалов из исследования [1]
|
Материал |
Предел текучести, МПа |
Предельное растягивающее напряжение, МПа |
Модуль упругости, ГПа |
|
Сталь (16 мм) |
560 |
707 |
205 |
|
Сталь (10 мм) |
500 |
574 |
200 |
|
Сталь (8 мм) |
400 |
586 |
200 |
|
CFRP ламинат |
- |
986 |
95,8 |
Прочие свойства, необходимые для численного моделирования балки, подбирались из литературных источников, а также, если определить их не представлялось возможным, принимались как средние для данных материалов. Далее будут представлены все свойства, заложенные в модели.
Для упрощения создания геометрии численной модели, фактические параметры балки, заносимые в программный комплекс, представлены ниже (рис. 2).
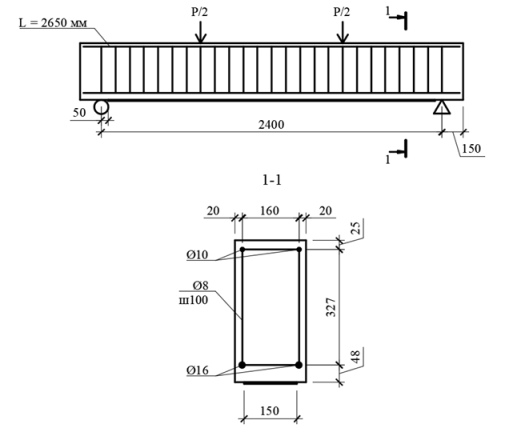
Рис. 2. Расчетная схема балки, разрез 1–1
Параметры защитного слоя приняты согласно [2], кроме толщины в растянутой зоне, она принята по схеме из эксперимента [1] (см. рис.1). Длина продольной арматуры принята исходя из необходимой величины защитного слоя бетона согласно п. 3.92 [2].
Моделирование балки
В программном комплексе были созданы две модели балки: C2.0 — балка без внешнего армирования, S2.0 — балка, армированная ФАП ламинатом.
Моделирование начинается с создания геометрии (модуль «Part», кнопка «Create part»). Были созданы следующие объекты (табл. 2):
Таблица 2
Геометрические параметры элементов модели
|
Наименование элемента |
Принятые имена |
Тип тела |
Размеры |
|
Бетонная балка |
Beam |
deformable, solid |
200x400x2700 (мм) |
|
Стержень продольной арматуры, диаметром 10 мм |
bar_10 |
deformable, wire |
L = 2650 мм А = 78,5 мм 2 |
|
Стержень продольной арматуры, диаметром 16 мм |
bar_16 |
deformable, wire |
L = 2650 мм А = 201,1 мм 2 |
|
Хомут |
stirrup |
deformable, wire |
160x327 (мм) А = 201,1 мм 2 |
|
Элемент передачи нагрузки/ опорный элемент |
plate |
deformable, solid |
50x10x200 (мм) |
|
ФАП ламинат |
FRP |
deformable, shell |
150x1x2300 (мм) |
Следующим этапом задаются свойства материалов (create property) в модули “Property”. Необходимо задать объемный вес (General — Density), модули упругости (и сдвига для ФАП) и коэффициенты Пуассона (Mechanical — Elasticity) (табл.3).
Таблица 3
Свойства материалов
|
Материал |
Свойства |
|||
|
Density |
Elastic |
Plastic |
||
|
Сталь для арматуры |
7,8х10– 5 H/мм 3 |
Е = 200000 МПа ν = 0,3 |
Yield Stress (МПа) |
Plastic Strain |
|
560 |
0 |
|||
|
707 |
0,0222 |
|||
|
Сталь для опорных элементов |
7,8х10– 5 H/мм 3 |
Е = 200000 МПа ν = 0,3 |
- |
|
|
ФАП |
1,56х10– 5 H/мм 3 |
E1 = 95800 МПа E2 = 10000 МПа Ν = 0.25 G12 = 5000 МПа G13 = 5000 МПа G23 = 5000 МПа |
- |
|
|
Бетон |
2,5х10– 5 H/мм 3 |
Е = 26600 МПа ν = 0,2 |
- |
|
Для того, чтобы получить картину трещинообразования бетона, необходимо вести критерии разрушения материала (Mechanical — Plasticity — Concrete Damaged Plasticity). Параметры бетона были приняты из [3] и представлены ниже в таблице 4.
Таблица 4
Свойства бетона
|
Material’s parameters |
Plasticity parameters |
||
|
Dilation angle |
31 |
||
|
Concrete Elasticity |
Eccentricity |
0.1 |
|
|
E (GPa) |
26.6 |
fb0/fc0 |
1.16 |
|
0.2 |
K |
0.67 |
|
|
Viscosity parameter |
0 |
||
|
Concrete compressive behavior |
Concrete compression damage |
||
|
Yield stress (MPa) |
Inelastic strain |
Damage parameter C |
Inelastic strain |
|
15.3 |
0 |
0 |
0 |
|
19.2 |
4.8249E-05 |
0 |
4.8249E-05 |
|
22.5 |
0.000119844 |
0 |
0.000119844 |
|
25.2 |
0.000214786 |
0 |
0.000214786 |
|
27.3 |
0.000333074 |
0 |
0.000333074 |
|
28.8 |
0.000474708 |
0 |
0.000474708 |
|
29.7 |
0.000639689 |
0 |
0.000639689 |
|
30 |
0.000828016 |
0 |
0.000828016 |
|
29.7 |
0.001039689 |
0.01 |
0.001039689 |
|
28.8 |
0.001274708 |
0.04 |
0.001274708 |
|
27.3 |
0.001533074 |
0.09 |
0.001533074 |
|
25.2 |
0.001814786 |
0.16 |
0.001814786 |
|
22.5 |
0.002119844 |
0.25 |
0.002119844 |
|
19.2 |
0.002448249 |
0.36 |
0.002448249 |
|
15.3 |
0.0028 |
0.49 |
0.0028 |
|
10.8 |
0.003175097 |
0.64 |
0.003175097 |
|
5.7 |
0.003573541 |
0.81 |
0.003573541 |
|
Concrete tensile behavior |
Concrete tension damage |
||
|
Yield stress (MPa) |
Cracking strain |
Damage parameter T |
Cracking strain |
|
3 |
0 |
0 |
0 |
|
0.03 |
0.001167315 |
0.99 |
0.001167315 |
Затем, в том же модуле, создаются сечения и присваиваются соответствующим элементам. Для листа ФАП задается составная структура функцией “Create Composite Layup”. Задаем количество слоев — 4. Region — указываем элемент FRP (выделяем соответствующий элемент в области модели), толщину слоев назначаем 0,25 мм, назначаем углы 0, 45, -45, 90.
В модули “Assembly” производим сборку элементов модели. Функцией “Create Instance” добавляем элементы. Используем “Linear Pattern”, “Translate Instance”, “Rotate Instance”, чтобы множить, перемещать и поворачивать элементы. Собранная модель представлена на рис. 3.
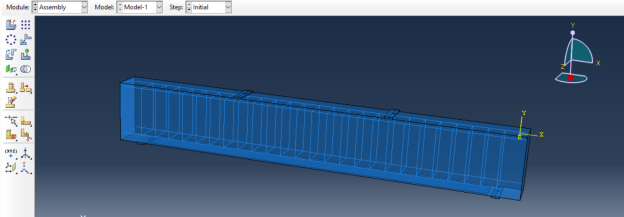
Рис. 3. Балка S2.0 в модуле Assembly
В модуле Step настраиваем процедуру расчета. Создаем новый шаг расчета (Create Step). Был выбран явный динамический анализ Dynamic, Explicit.
К выходным данным добавлены переменные demaget (разрушение по растянутым волокнам) / demagec (разрушения по сжатым волокнам) (Field Output Manager — Edit — Failure/Fracture).
Модуль Interaction предназначен для задания взаимодействий между телами. Связь между бетоном и арматурой задавалась как embedded region. Тип взаимодействия между Бетон — ФАП — tie. Между бетоном и стальными брусками в нормальном направлении задана жесткая связь, в продольном направлении задан коэффициент жесткости 0,35.
В модуле “Load” были заданы условия опирания, нагрузка задана распределенной по поверхности стальных брусков и равна 12,3 МПа.
Каждый элемент модели в отдельности разбивался на сетку конечных элементов (модуль “Mesh”). Балка и стальные бруски имеют тип конечного элемента C3D8R, арматурные стержни — T3D2, ФАП ламинат — S4R.
Результаты расчета
На рис. 4 представлена фотография балки после натурного испытания [1]. На рис. 5 представлено разрушение по растянутому бетону балки, замоделированной в программном комплексе.

Рис. 4. Балка С2.0 при натурном испытании
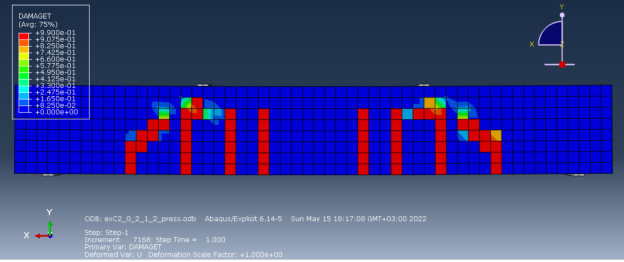
Рис. 5. Балка С2.0 в Abaqus
Характер распространения трещин схож. Имеются как нормальные, так и наклонные трещины, развитые по высоте сечения.
На рис. 6 представлена балка с усилением.
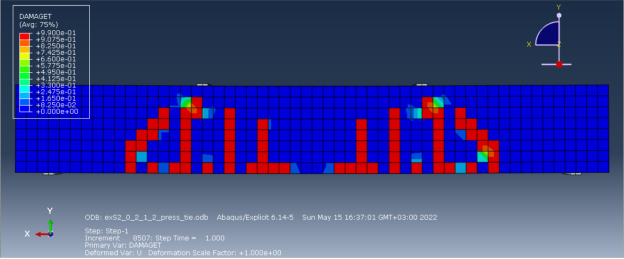
Рис. 6. Балка S2.0 в Abaqus
Характер распространения нормальных и наклонных трещин аналогичен, однако у растянутой грани балки наблюдается растрескивание бетона, что еще более наглядно можно увидеть на рис. 7.
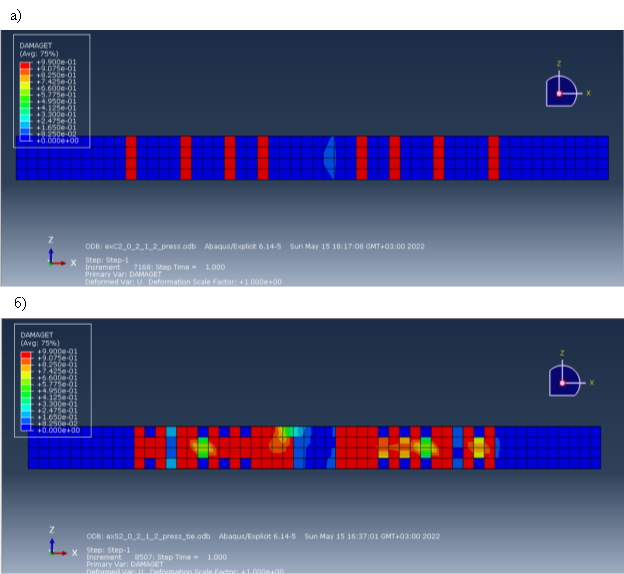
Рис. 7. Нижняя грань балки а) С2.0 и б) S2.0.
Выводы
Полученная в результате моделирования железобетонной балки в программном комплексе Abaqus картина трещинообразования согласуется с результатами лабораторных испытаний. Учитывая тот факт, что большое количество параметров материалов были приняты самостоятельно, сходимость можно считать вполне удовлетворительной.
Трещины в балке с усилением развились аналогично, что и в балке без усиления, кроме зоны вблизи растянутой грани бетона, где наблюдается большее дробление. Что, впрочем, можно объяснить обжатием бетона ФАП ламинатом.
Литература:
- Al-Saawani, M. A. Effect of shear-span/depth ratio on debonding failures of FRP-strengthened RC beams / M. A. Al-Saawani, A. K. El-Sayed, A. I. Al-Negheimish. — Текст: непосредственный // Journal of Building Engineering. — 2020. — № 32.
- Руководство по конструированию бетонных и железобетонных конструкций из тяжелого бетона (без предварительного напряжения) МОСКВА СТРОЙИЗДАТ 1978. — Текст: электронный // files.stroyinf.ru: [сайт]. — URL: https://files.stroyinf.ru/Data2/1/4293855/4293855202.htm (дата обращения: 16.05.2022).
- Simplified Damage Plasticity Model for Concrete / M. Hafezolghorani, F. Hejazi, R. Vaghei, M. Jaafar. — Текст: непосредственный // Structural Engineering International. — 2017. — № 1. — С. 68–78.







