Система подсчета заданных объектов на изображении — система, получающая на вход изображение и массив параметров, по которым будут подсчитаны «ключевые» объекты на изображении.
Ключевые слова: классификация, методы обнаружения.
В настоящее время происходит большое кол-во массовых мероприятий в зависимости от кол-ва участвующих должны быть проведены некоторые меры обеспечения безопасности присутствующих и окружения. Для этого необходимо узнать конкретное кол-во участвующих людей. Необходимо это для МВД, транспортных служб, медицинских организаций. Аналогичная задача возникает при разработке различного вида химических пленок, пластических материалов, металлов. Для определения их качеств необходимо знать количество частиц на единицу площади. Для этих целей будет написана программа, использующая алгоритмы «старой школы» детектирования объектов.
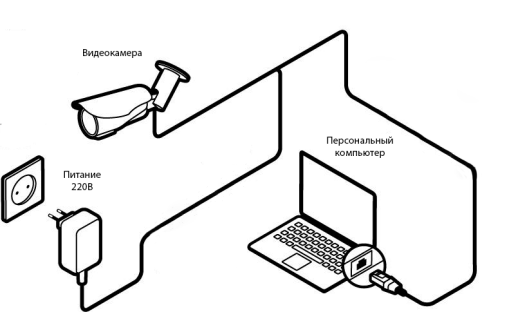
Рис. 1. Схема системы подсчета объектов
Так как входное изображение содержит слишком много дополнительной информации, первым шагом в классификации изображений является упрощение изображения путем извлечения важной информации, содержащейся в изображении, и исключения остальной части. Например, если мы хотим найти на изображениях пуговицы рубашек и пальто, то заметим значительные различия в значениях пикселей RGB. Однако, запустив детектор краев изображения, можно упростить изображение. Вы все еще можете легко различить круглую форму кнопок на этих изображениях краев, и поэтому мы можем сделать вывод, что обнаружение краев сохраняет важную информацию, отбрасывая несущественную информацию. Этот шаг называется извлечением признаков. В традиционных подходах к компьютерному зрению разработка этих функций имеет решающее значение для производительности алгоритма. Оказывается, мы можем сделать намного лучше, чем простое обнаружение краев, и найти функции, которые намного надежнее.
Для того, чтобы система проще определяла края необходимых нам объектов, будет применяться фильтр Гаусса. Фильтр Гаусса является самым простым с математической точки зрения. Спектральные составляющие этого типа шума равномерно распределены по всему диапазону задействованных частот. Примерами белого шума являются водопадный шум или статический шум. В природе и технике «чисто» белый шум (то есть белый шум, имеющий одинаковую спектральную мощность на всех частотах) не встречается (в силу того, что такой сигнал имел бы бесконечную мощность), однако любой шум, спектральная плотность которого одинакова (или несколько отличается) в рассматриваемом диапазоне частот. Функция плотности распределения Гауссового шума случайной величины z имеет вид:
p(z)=1√2πσe−(z−μ)2/2σ2
где z (применительно к тематике данной работы) есть значение яркости,
μ — среднее значение случайной величины z ,
σ — ее среднеквадратичное отклонение.
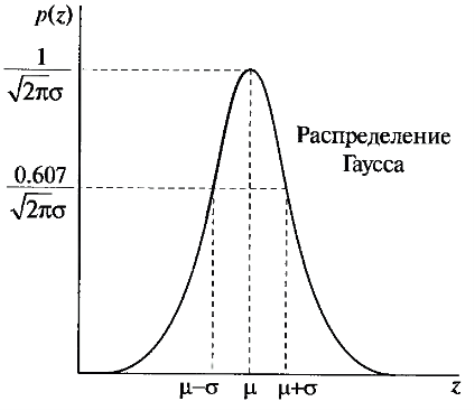
Рис. 2. График плотности распределения Фильтра Гаусса
После фильтрации, можно перейти к определению искомых объектов, для этого изображение переводится в полутон, в таком случае с помощью метода Оцу можно определить коэффициент бинаризации.
Метод Оцу — это алгоритм вычисления порога бинаризации для полутонового изображения, используемый в области компьютерного распознавания образов и обработки изображений для получения чёрно-белых изображений. Алгоритм позволяет разделить пиксели двух классов («полезные» и «фоновые»), рассчитывая такой порог, чтобы внутриклассовая дисперсия была минимальной.
Метод Оцу использует гистограмму изображения для расчета порога, где гистограмма — это набор бинов, каждый из которых характеризует количество попаданий в него элементов выборки. В нашем случае выборка — это пиксели различной яркости, которая может принимать целые значения от 0 до 255. По гистограмме можно определить, что имеется два четко разделяющихся класса. Суть метода Оцу заключается в том, чтобы выставить порог между классами таким образом, чтобы каждый их них был как можно более «плотным». Для этого все сводится к минимизации внутриклассовой дисперсии, которая определяется как взвешенная сумма дисперсий двух классов:
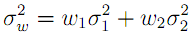
Оцу показывает, что минимизация внутриклассовой дисперсии эквивалента максимизации межклассовой дисперсии:
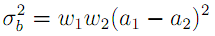
Так как w1(t + 1), w2(t + 1), a1(t + 1), a2(t + 1) легко выражаются через предыдущие значения w1(t), w2(t), a1(t), a2(t) (где t — текущий порог, а T- искомый), можно легко составить алгоритм быстрого определения искомого порога:
— Вычисляем гистограмму.
— Начиная с порога t = 1, проходим через всю гистограмму, на каждом шаге пересчитывая дисперсию σb(t). Если на каком-то из шагов дисперсия оказалась больше максимума, то обновляем дисперсию и T = t.
— Искомый порог равен T.
К недостаткам метода Оцу относятся:
— размытие линий
— «слипание» объектов, особенно в местах пересечений
— потеря тонких линий
Наконец, когда порог определен, можно переводить изображение в бинарный вид, где проще всего подсчитать объекты и определить их ограничивающие рамки.
Ниже приведены результаты работы программы.

Рис. 3. Исходное изображение
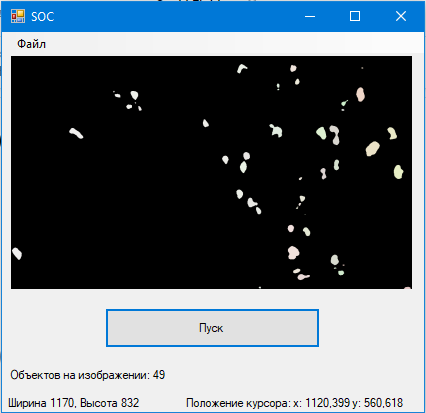
Рис. 4. Бинаризированное изображение методом Оцу
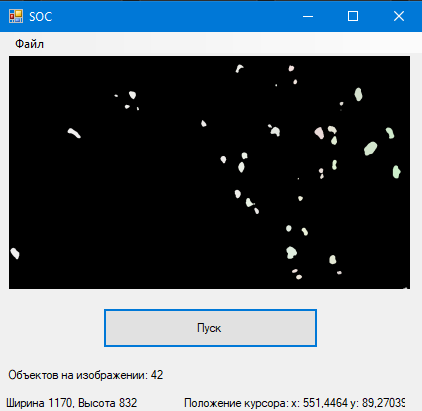
Рис. 5. Бинаризированное изображение ручным подбором порога
По изображениям видно, что на данном этапе система работает не идеально и местами сливает объекты в один, так же объекты не выделяются «рамками объекта», а лишь получают уникальный цвет. Разброс подсчета слишком велик и составляет около 5–10 %, что крайне критично для такого приложения.
Ручной подбор дал более точный подсчет, его разброс равен всего 3 %
Все это будет доработано и исправлено для более точного подсчета объектов.
Литература:
- Рафаэл С.Гонсалес. Мир цифровой обработки: Пер. с англ. 2012–860с
- textarchive. Различные реализации Гауссова фильтра [Электронный ресурс]: URL.: https://textarchive.ru/c-2836819.html свободный — (дата обращения 12.04.2022)
- bmstu.wiki. Предварительная обработка изображений [Электронный ресурс]:URL.: https://ru.bmstu.wiki/Предварительная_обработка_изображений свободный — (дата обращения 12.04.2022)
- Кравцова Т. А. Сравнительное исследование методов адаптивной бинаризации в задаче автоматизированного анализа изображений клеток в иммуноцитохимии. Молодежный научно — технический вестник, 2015.
- Янковский Александр Аркадиевич, Бугрий Андрей Николаевич. Критерии выбора метода бинаризации при обработке изображений лабораторных анализов // АСУ и приборы автоматики. [Электронный ресурс], 2010. № 153. Режим доступа: http://cyberleninka.ru/article/n/kriterii-vybora-metoda-binarizatsiipri-obrabotke-izobrazheniy-laboratornyh-analizov/ (дата обращения: 21.05.2017).







