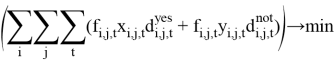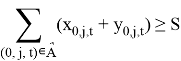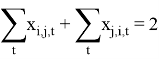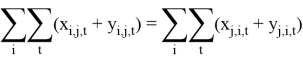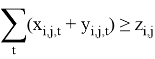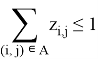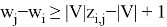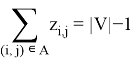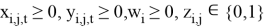Математическая постановка задачи маршрутизации снегоуборочных машин со штрафами за поворот



В работе приводится описание задачи маршрутизации снегоуборочных машин со штрафами за поворот, а также представлена авторская математическая постановка для решения данной задачи.

Ключевые слова : маршрутизация, граф, математическая постановка, остовное дерево.

В зимнее время распространенной задачей является определение оптимального маршрута снегоуборочных машин, чтобы минимизировать пройденное ими расстояние. Обычно она представлена как задача дуговой маршрутизации, которая стремится найти маршрут минимальной длины, пересекающий требуемые дуги графа G. В рамках данной работы мы учитываем, что во время движения снегоуборщика предпочтительнее определенный тип поворота на перекрестке. Поворот направо или движение прямо часто предпочтительнее, потому что это занимает меньше времени, безопаснее и в случае движения с уборкой снега, не приводит к его попаданию на центр перекрестка. Левые повороты и развороты часто не рекомендуются, так как они занимают больше времени и сдвигают снег на центр перекрестка [1, 2].

Рассмотрим граф G = {V, E}, где множество вершин V = { } и множество ребер E ⊆ {( , ) | , ∈ V, i < j}. Каждое ребро ( ,

) имеет четыре стоимости: — стоимость уборки улицы от до , — стоимость уборки улицы от до , — стоимость перехода от к без уборки снега и — стоимость перехода от

к без уборки снега. Если предположить, что вершина имеет большую высоту, чем вершина , то обычно > > > . Мы ищем маршрут, который начинается и заканчивается в депо ( ), дважды проезжаем с уборкой от снега по каждой необходимой улице (для каждой ее стороны) и сводим к минимуму суммарную стоимость маршрута [1, 3].

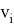
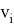
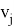
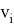
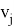
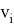
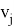
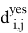
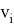
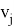
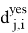
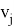
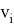
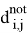
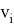
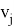
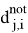
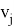
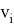
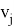
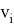
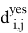
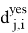
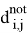
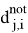
Чтобы сформулировать постановку, учитывающую штрафы за повороты, мы рассматриваем кроме графа G новый граф . Вместо дуг, представляющих движение от перекрестка i к перекрестку j, дуги

представляют движение от перекрестка i к перекрестку j и поворот в сторону перекрестка t [1]. Проиллюстрируем это на рисунке 1.

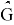
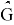
Рис. 1. Пример графа поворотов

Определим следующие переменные и константы для нашей постановки:

— — количество проездов с уборкой снега по дуге (i, j, t);

— — количество проездов по дуге (i, j, t) без уборки снега;

— — стоимость проезда с уборкой снега по дуге (i, j, t);

— — стоимость проезда по дуге (i, j, t) без уборки снега;

— = 1, если дуга (i, j) графа G входит в остовное дерево, иначе 0;

— ‒ штраф за выполнение поворота по дуге (i, j, t), ;

— ‒ потенциал вершины графа G;

—

‒ набор дуг графа ;

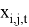
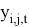
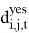
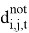
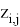
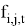
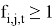
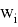
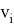
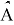
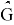
— E ‒ набор ребер графа G;

— S ‒ количество снегоуборщиков;

— V ‒ набор вершин графа G;

— A ‒ набор дуг графа G.

Задача определяется следующим образом:

(1)

при условии выполнения следующих ограничений

(2)

депо должно покинуть S машин

(3)

∀ (i, j) ∊ E

(4)

∀ j

(5)

∀ (i, j) ∊ A

(6)

∀ j

(7)

∀ (i, j) ∊ A

(8)

необходимо обеспечить целочисленность и неотрицательность переменных

(9)

∀ (i, j, t) ∊ , ∀ (i, j) ∊ A, ∀ i ∊ V, ∊ Z, ∊ Z

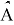
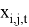
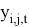
Целевая функция (1) минимизирует стоимость маршрута с учетом проездов по улицам как с уборкой снега, так и без нее. Изменение параметра может усилить или ослабить штрафы за поворот. Значение данного параметра всегда равняется единице для дуг, обозначающих повороты направо или прямые проезды через перекресток. Для дуг, обозначающих повороты налево или развороты на перекрестке, значение параметра может быть настолько больше единицы, насколько сильнее необходимо усилить штраф за данные повороты. Ограничение (2) требует, чтобы любой маршрут покидал депо по крайней мере S раз, гарантируя, что существует достаточное количество подциклов для распределения между S снегоуборщиками. Ограничение (3) вынуждает очищать каждую требуемую улицу дважды, по одному разу для каждой стороны. Ограничение (4) требует, чтобы полустепень исхода каждой вершины графа G была равна ее полустепени входа. Ограничение (5) необходимо для того, чтобы маршрут обязательно проходил по дугам, входящим в остовное дерево. Ограничение (6) требует, чтобы из каждой вершины остовного дерева выходило не более одной дуги. В ограничении (7) потенциалы вершин предотвращают образование подциклов в остовном дереве. Ограничение (8) необходимо, потому что в остовном дереве количество дуг на одну меньше количества вершин. Ограничение (9) обеспечивает неотрицательность и целочисленность переменных.

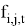
Ограничения (6, 7, 8) обеспечивают построение остовного дерева, которое необходимо вместе с ограничением (5) для обеспечения устранения несвязанных циклов. Проиллюстрируем это на рисунке 2.

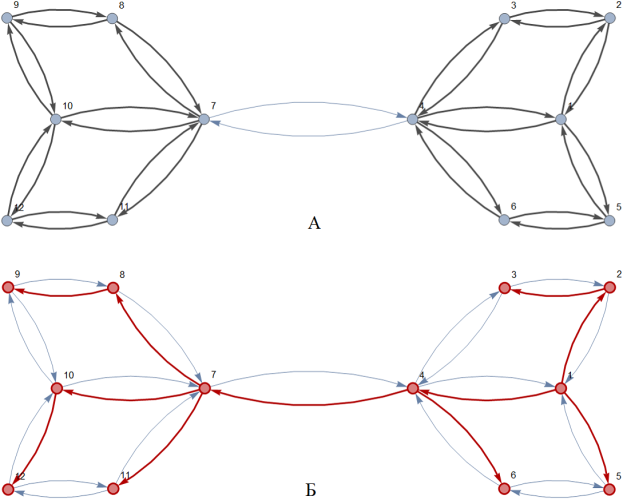
Рис. 2. Дуги графа, которые необходимо посетить с уборкой от снега (А) и остовное дерево (Б)

На рисунке 2 (А) представлен граф. В нем выделенные дуги соответствуют улицам, которые необходимо проехать с уборкой от снега. Без ограничений (5, 6, 7, 8) маршрут распадется на 2 несвязанных цикла, так как мы минимизируем стоимость маршрута и дуги (4, 7), (7, 4) не являются обязательными для прохождения. На рисунке 2 (Б) представлено остовное дерево, связывающее эти два цикла в единый маршрут при помощи ограничения (5), которое заставляет включить в маршрут дуги, входящие в остовное дерево.

Литература:

1. Benjamin Dussault, Modeling and solving arc routing problems in street sweeping and snow plowing, 2012.
2. Carmine Cerrone, B. Dussault, Xingyin Wang, B. Golden, E. Wasil, A two-stage solution approach for the Directed Rural Postman Problem with Turn Penalties, 2019.
3. Michael Drexl, On the generalized directed rural postman problem, 2014.