В статье произведено описание прицепа действия вибровискозиметра, показана схема датчика, произведен теоретический анализ собственных частот колебаний, выполнено сравнение полученных результатов с экспериментальными данными.
Ключевые слова: вибровискозиметр, собственная частота, колебания, сенсор.
Объектом для анализа свободных колебаний является вибровизкозиметр, созданный в УФИРЭ им. В. А. Котельникова для исследования вязкости многокомпонентных растворов. Схематично принцип действия датчика можно описать рисунком 1. Чувствительная (колебательная) масса подвешена на капиллярах.
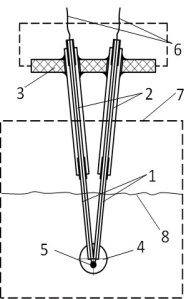
Рис. 1. Конструкция вибровизкозиметра: 1 — капилляр, 2 — пьезотрубки, 3 — статор, 4 — измерительный блок, 5 — датчик температуры, 6 — элементы выводного монтажа, 7 — исследуемая жидкость, 8 — пороговый уровень
Система возбуждения построена на основе пьезодвигателей, которые запитываются напряжением с нужной частотой. Численно она равна собственной частоте колебаний. Плоскость колебаний перпендикулярна плоскости, которую образуют трубки. Одна трубка выступает активатором, вторая — сенсором. Колебания трубки снимаются пьезодатчиком и представляют собой электрический заряд, который находится в прямой зависимости от амплитуды колебаний, которая, в свою очередь, пропорциональна вязкости.
С точки зрения теоретической механики, колебательная система, состоящая из нескольких звеньев, очень сложно поддается правильному и достоверному теоретическому расчету. В связи для проведения более точных расчетов используем САПР Mathcad.
На начальном этапе проектирования необходимо выполнить анализ свободных колебаний частей системы. Для создания этих колебаний достаточно отклонить от положения равновесия любой элемент системы. На рисунке 2 представлен график затухающих колебаний. На графике М1 — это возбуждающее колебание зонда, М01 и М02 — свободные колебания системы возбуждения и пьезосенсора.
Из графика видно, что колебания представляют собой набор гармоник и для выделения собственной частоты необходимо провести спектральный анализ данных сигналов. Это позволит оценить спектр свободных колебаний.
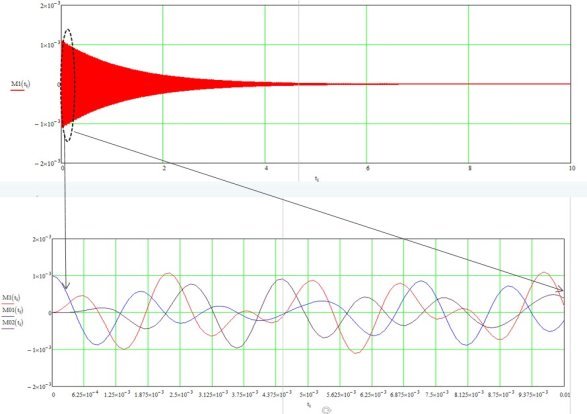
Рис. 2. Спектры колебаний
Такой сложный вид гармонических колебаний связан с особенностями расчета, сканирование по широкому спектру резко увеличивает время расчёта. Широкий диапазон обусловлен отсутствием достоверных данных о частотных характеристиках объекта. Для упрощения спектра используем классическое преобразование Фурье (рисунок 3,4). Максимумы (пики) — это частоты гармоник собственных колебаний частей системы.
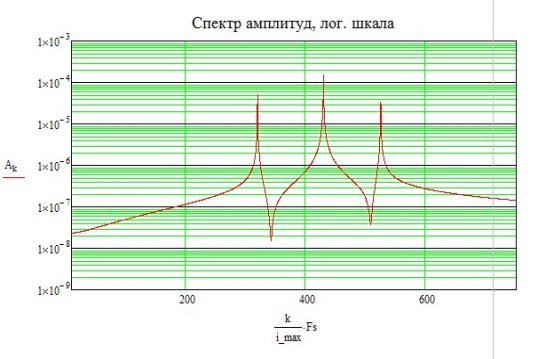
Рис. 3 Преобразование Фурье (логарифмическая шкала)
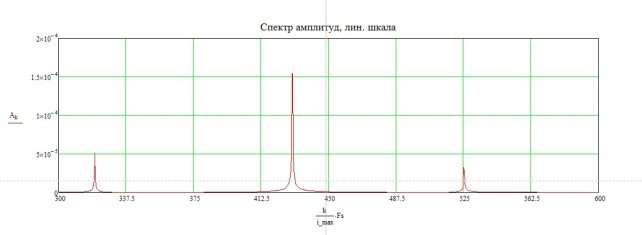
Рис. 4 Преобразование Фурье (линейная шкала)
Для определения соответствия каждого резонансного пика определенной части системы в модели производилось изменение массы с последующим анализом частотного смещения собственных гармоник после преобразования Фурье. По результатам моделирования установлено, что собственная частота зонда — 320–335 Гц (рисунок 5). Частота пьезодвигателя — 425–445 Гц (рисунок 6). Красный график описывает колебательную систему до изменения, синий — измененную систему.
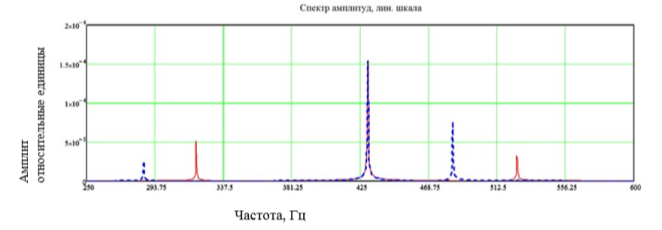
Рис. 5. Спектр зонда
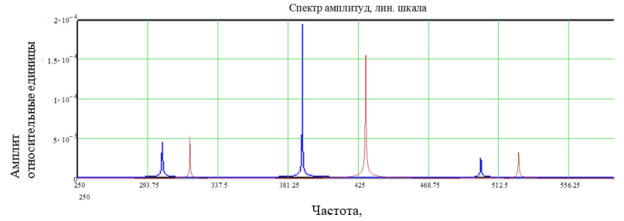
Рис. 6. Спектр пьезодвигателя
Конечным результатом эксперимента является сравнение полученной модели свободных колебаний с экспериментальными данными. Результаты данного сравнения показаны на рисунках 7 и 8.
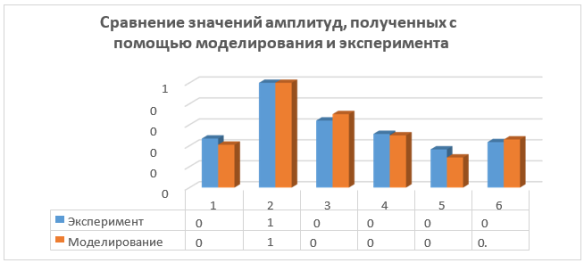
Рис. 7. Сравнение амплитуд свободных колебаний
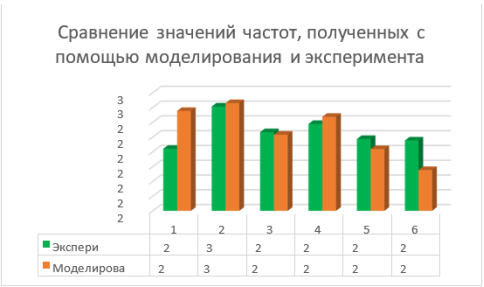
Рис. 8. Сравнение частот свободных колебаний
Проанализировав полученные результаты, можно сделать вывод о том, что экспериментальные данные и данные, полученные в процессе моделирования, в большей степени соответствуют, но также наблюдаются расхождения у некоторых жидкостей, т. к. их физические свойства находятся в прямой зависимости от температуры, влажности, что нельзя учесть при моделировании.
Литература:
1. Соломин Б. А. Миниатюрный высокочувствительный и быстродействующийвибровискозиметрический датчик/ Б. А. Соломин, А. М. Низаметдинов, А. А. Черторийский, М. Л. Конторович // Конструирование и производство датчиков, приборов и систем — 2015 — С. 3–8.
2. Г. Ф. Афанасьева. Вискозиметры стеклянные капиллярные образцовые. Методы и средства поверки/методические указания// — 1984 — С. 20–21.







