Проектирование алгоритмов приложения распознавания речи на основе вейвлет-анализа



В статье автор рассматривает проектирование алгоритмов приложения распознавания речи на основе вейвлет-анализа.

Ключевые слова: вейвлет-анализ, распознавание речи, преобразование Фурье, мел-кепстральные коэффициенты.

Рассмотрим практику применения распознавания сигналов в системах распознавания речи.

Язык может быть описан как категория абстрактных лингвистических единиц, называемых фонемами. Фонема — наименьший (обладающий смыслом) элемент этой категории. Композиция морфизмов фонем может быть использована для формирования слов в этом языке.

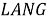
Следует различать понятие «фонема» и «фонетический элемент». Фонема — базовая единица языка в лингвистическом определении, и возможность ее взаимно-однозначного соответствия с фонетическим элементом в акустическом пространстве неявна, то есть фонема может быть представлена более чем одним фонетическим элементом [1].

Выделяют следующие параметры характеристик фонем:

1. Существует значимое различие между классами характеристик.
2. Характеристика стабильна на протяжении довольно длительного времени.
3. Характеристика может быть вычислена за конечное время по образцу речи.
4. Характеристика должна обладать малой размерностью.
5. Характеристика должна быть независима от сторонних шумов и от искажений.
6. У характеристики не должно быть корреляций с другими характеристиками.

Рассмотрим методы выделения характеристик речи.

Для описания частотной области речевых сигналов часто используется быстрое преобразование Фурье (БПФ) [2]. Коэффициенты БПФ могут быть использованы для выделения частот формант [3] (термин фонетики, обозначающий акустическую характеристику звуков речи — прежде всего гласных — связанную с уровнем частоты голосового тона) . Частоты форманта — пиковые частоты резонанса голосового тракта, где

— самая низкая (по резонансу) частота.

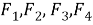
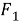
Использование быстрого преобразования Фурье предполагает, что сигнал стационарный, однако в задачах обработки речи это не всегда так. Для преодоления этого недостатка сигнал анализируется меньшими подынтервалами (фреймами). Длительность фрейма может быть гораздо короче длительности фонемы, обычно она составляет 10–20 мс. В таких временных промежутках сигнал можно считать стационарным. Для подсчета коэффициентов БПФ в данной длительности фрейма использует оконное преобразование Фурье (Short Time Fourier Tranform) [4] — Фурье-преобразование на малом временном интервале, которое определяет частоту компонентов сигнала в завимости от длительности фрейма.

Основным недостатком STFT является фиксированное разрешение. Ширина оконной функции соотносится с представлением сигнала — она определяет существование достаточного разрешения частоты (лежащие близко друг к другу компоненты можно разделить) или достаточно хорошее разрешение времени (определяется как время, с которым меняется частота). Использование широкого окна дает преимущество в виде разрешения, но ухудшает показатели времени. Узкое окно дает преимущество в виде времени, но ухудшает показатели разрешения. Такое свойство связано (не напрямую, вводится через предел Габора [5]) с принципом неопределенности Гейзенберга, который гласит:

,(1.1)

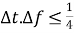
где —разрешение времени;

— разрешение частоты.

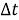
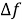
На рисунке 1 показана частотно-временная замощенная STFT плоскость.

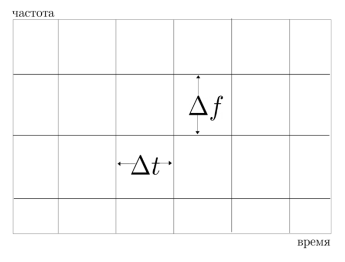
Рис. 1. Частотно-временная плоскость, замощенная с использованием STFT

Фурье-преобразования на малом временном интервале используется в большинстве систем распознавания речи для выявления речевых характеристик. Предположение о стационарности сигнала верно в большинстве случаев, за исключением фонем, звучащих при остановке речи. Фиксированное отношение «время-частота» (рисунок 1) также налагает ограничения при использовании STFT (функции разложения по базису локальны по частоте, но не по времени).

Очевидное решение проблемы — использовать адаптивный размер окна. (больше времени для низких частот и меньше времени для высоких).

Вейвлет-преобразование — частотно-временное преобразование, с помощью которого можно анализировать как нестационарные, так и стационарные сигналы.

На рисунке 2 показаны различия между использованием вейвлет-преобразования и STFT на временно-частотной плоскости.

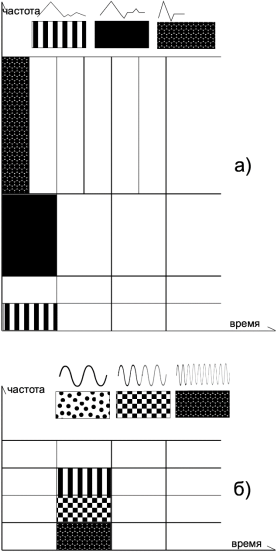
Рис. 2. Замощение временно частотно-плоскости с использованием: а) вейвлет-преобразования, б) TSFT

Мел-кепстральные коэффициенты используются для получения представления одного временного окна до конечного числа коэффициентов, каждый из которых вносит значительный вклад в конечный спектр [6].

Мел-кепстральные коэффициенты (MFCC) основываются на линейных предиктивных коэффициентах. Главным преимуществом MFCC является независимость коэффициентов друг от друга.

Кепстральные коэффициенты также могут быть вычислены с помощью быстрого преобразование Фурье (на вход поступают речевые семплы) и его перевода в логарифмическую шкалу. Человеческое восприятие частоты звука нелинейно, для каждого тона с частотой Гц субъективный тон отмеряется на шкале «Мел».

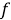
На рисунке 3 изображено отображение шкалы Герца в шкалу «Мел».

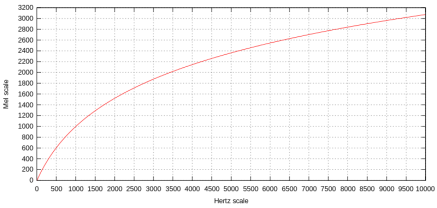
Рис. 3. Отображение шкалы Герца в шкалу «Мел»

Математически шкала определяется как

(1.2)

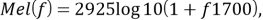
где —в герцах.

Шкала «Мел» используется с 1980-х годов для разработки структур полосовых фильтров для извлечения характеристик, основанных на MFCC.

Характеристики, полученные с помощью MFCC, удобны для отделения спектра гласных звуков для лучшего распознавания речи.

Большинство приложений распознавания речи можно свести к алгоритму сопоставления преобразованного в дигитальный вид сигнала к образцу.

Разработка данного приложения сводится к реализации алгоритмов подготовки звука — MFCC (создание эталона) и DWT — для тренировки звуковой модели и их комбинации в алгоритм, представленный на рисунке 4.

Архитектура приложения показана на рисунке 4.

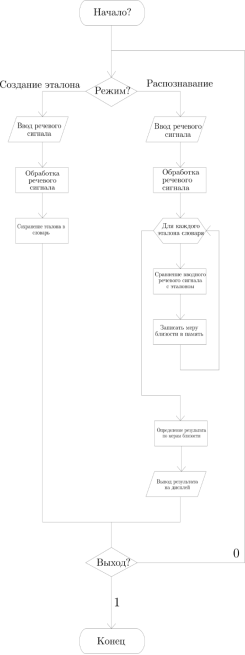
Рис. 4. Архитектура программного приложения распознавания речи

Метод распознавания мел-кепстральных коэффициентов чаще всего состоит из нескольких подпроцессов. Первый называется «предварительное выделение», его смысл заключается в увеличении уровня энергий в высоких частотах. Поскольку на нижних частотах содержится больше энергии, чем на верхних, наличие большего количества данных на высоких частотах может увеличить качество обработки сигнала. Перепад энергий между низкими и высокими частотами, вызванный гортанной смычкой, называется спектральным отражением.

Второй процесс называется «экранирование». Небольшие окна (длиной от 20 до 25 мс) применяются к речевому сигналу с 10 мс смещением фрейма в целях симуляции кусочной стационарности сигнала. Фонемы имеют длину больше трех окон, поэтому кусочная стационарность сигнала сохраняется и для окон. Процесс выделения характеристик применяется каждый раз с целью получения коэффициентов в каждом окне. У коэффициентов будет более высокое разрешение по времени при маленьком окне и малое разрешение по времени при большом.

Третий подпроцесс называется дискретным преобразованием Фурье, оно определяется как

(1.3)

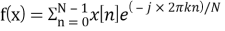
Для реализации алгоритма чаще всего используется быстрое преобразование Фурье. БПФ снижает вычислительную сложность алгоритма с квадратичной до логарифмической — с до , где — размер данных.

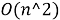
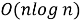
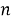
Четвертый подпроцесс называется «Применение мел-полосовых фильтров и взятие логарифма. Шкала делит или сжимает частоты в группы, воспринимаемые слушателем одинаково. Шкала «Мел» линейна на частотах до одного килогерца, но схожа по порядку роста с логарифмом на частотах свыше килогерца. Реализация может быть достигнута использованием полосовых фильтров со сканированием групп частот.

Пятый подпроцесс называется обратное дискретное преобразование Фурье — оно определяется как обратное ДПФ логарифма ДПФ сигнала.

Шестой подпроцесс — подсчет дельт и энергии. Энергия определяется как

(1.4)

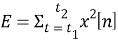
где —начало фрейма,

— конец фрейма.

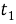
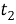
Дельты подсчитываются как разницы между соседними фреймами каждого элемента кепстрального вектора.

В результате выполнения алгоритма на выход поступают кепстральные коэффициенты с дельтами, которые могут быть использованы в качестве входа системы распознавания речи.

Дискретное вейвлет-преобразование разбивает сигнал с помощью фильтров низких и высоких частот. Пусть — выход фильтра высоких частот, а — выход фильтра низких частот. Если предположить, что сэмплированный сигнал мощностью 16 кГц разбит на 10000 точек сэмплирования, то у первых коэффициентов группа частот будет находиться в пределах от 8 кГц до 16 кГц с пятью тысячами точек сэмплирования, у вторых — от 4 кГц до 8 кГц с 2500 точек сэмплирования, у третьих — от 0 кГц до 2 кГц с 1250 точками сэмплирования.

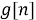
Преобразованный сигнал поступает на вход классификатора языковой модели.

На рисунке 5 изображен процесс трехуровневого стационарного вейвлет-преобразования.

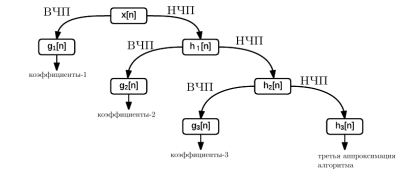
Рис. 5. Трехуровневое стационарное дискретное вейвлет-преобразование

Литература:

1. S. Young, «A review of large vocabulary continuous speech recognition», IEEE Signal Processing Magazine, September, pp. 45–57, 1996.

2. Галанина Наталия Андреевна, Алексеев Александр Георгиевич, Серебрянников Александр Владимирович Вычисление быстрого преобразования Фурье с использованием технологии cuda // Вестник ЧГУ. 2018. № 1. URL: https://cyberleninka.ru/article/n/vychislenie-bystrogo-preobrazovaniya-furie-s-ispolzovaniem-tehnologii-cuda (дата обращения: 05.04.2022).
3. Иванов Андрей Валерьевич, Трушин Виктор Александрович, Маркелова Гузель Викторовна, Рева Иван Леонидович ИССЛЕДОВАНИЕ СПЕКТРА ФОРМАНТ ФОРСИРОВАННОЙ РЕЧИ // Системы анализа и обработки данных. 2015. № 4 (61). URL: https://cyberleninka.ru/article/n/issledovanie-spektra-formant-forsirovannoy-rechi (дата обращения: 05.04.2022).
4. Савков А. А. Методы частотно-временного анализа электроэнцефалографических сигналов // Вестник Херсонского национального технического университета. 2014. № 3 (50). URL: https://cyberleninka.ru/article/n/metody-chastotno-vremennogo-analiza-elektroentsefalograficheskih-signalov (дата обращения: 05.04.2022).

5. Агафонов Андрей Валерьевич, Рожина Дарья Сергеевна, Модификация фильтра Габора для применения к цифровым изображениям дактилоскопических узоров // Евразийский научный журнал. 2017. № 8. URL: https://cyberleninka.ru/article/n/modifikatsiya-filtra-gabora-dlya-primeneniya-k-tsifrovym-izobrazheniyam-daktiloskopicheskih-uzorov (дата обращения: 05.04.2022).

6. Hanilçi, Cemal & Ertas, Figen & Ertas, Tuncay & Eskidere, Ömer. (2012). Recognition of Brand and Models of Cell-Phones From Recorded Speech Signals. IEEE Transactions on Information Forensics and Security. 7. 10.1109/TIFS.2011.2178403.