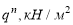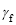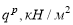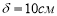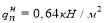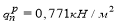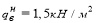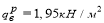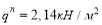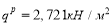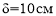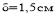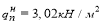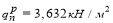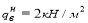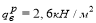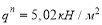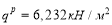В статье рассматривается сравнение аналитического и численного методов расчета сталежелезобетонного перекрытия для обоснования важности учета пространственной работы элементов перекрытия и их нелинейных свойств.
Ключевые слова: сталежелезобетон, совместная работа, нелинейность, составное сечение, приведенное сечение.
Введение
Из-за стремления строительных организаций к сокращению финансовых затрат на строительство, материалоемкости и трудоемкости появляется необходимость в улучшении качеств строительных материалов. Одним из ярких примеров такого улучшения является использование совместной работы стали и железобетона.
Несмотря на наличие богатой нормативной базы по расчету и проектированию сталежелезобетонных конструкций, существует необходимость в обосновании значимости нелинейности при расчете таких конструкций. Методика расчета [1]–[4] не позволяет в полной мере определить величину прогибов и в целом напряженно-деформационное состояние конструкции. Данный метод расчета можно учесть в численном расчете, используя различные программные комплексы.
Опыт использования сталежелезобетонных конструкций показывает развитие прогибов и перемещение в течение определенного времени. В некоторых случаях такие деформации приводят к разрушению конструкции. Поэтому при проектировании и расчете сталежелезобетонных конструкций необходимо учитывать нелинейные свойства железобетона.
Целью настоящих исследований является обоснование важности в той или иной степени учета нелинейных характеристик материалов при расчетах на прочность сталежелезобетонных конструкций зданий и сооружений.
Основная часть
1. Расчет сталежелезобетонного перекрытия
Расчет сталежелезобетонного перекрытия сводится к расчету составного сечения сталежелезобетоной балки и производится по двум стадиям: возведения и эксплуатации.
1.1. Аналитический расчет сталежелезобетонной балки составного сечения на стадии возведения
На стадии возведения конструкции (бетонировании) стальная балка является несущей конструкцией, работающей на поперечный изгиб. До набора прочности бетона в 50 % стальные балки необходимо рассчитывать на прочность и жесткость как стальной элемент в соответствии с СП 16.13330.2017 [1].
В случае с технологией комбинированной сталежелезобетонной конструкции на стальную балку будет давить лишь часть веса бетонной смеси и собственный вес балки [4]. В рамках статьи возьмем ¼ от веса бетонной смеси, который давит на конструкцию опалубки и стальной балки в целом. Также необходимо учитывать, что во время возведения конструкции по балкам могут ходить рабочие, следовательно, необходимо задать полезную нагрузку. Собственный вес балки условно примем равным
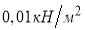
Принимаем условно балочную клетку с шагом стальных балок равным 1м и длиной пролета 6м.
Таким образом задаемся нагрузками, воздействующими на стальную двутавровую балку (таблица 1).
Таблица 1
Сбор нагрузок на стальную балку
|
№ п/п |
Вид нагрузки |
Нормативная нагрузка
|
|
Расчетная нагрузка
|
|
Постоянная |
||||
|
1 |
Собственный вес стальной балки |
0,01 |
1,05 |
0,011 |
|
2 |
Вес бетонной смеси (
|
0,63 |
1,2 |
0,76 |
|
Итого |
|
|
||
|
Временная |
||||
|
3 |
Полезная нагрузка |
1,5 |
1,3 |
1,95 |
|
Итого |
|
|
||
|
Всего |
|
|
||
Определяем интенсивность нормативной и расчетной равномерно распределенных нагрузок, действующих на балку (1.2, 1.3 соответственно):
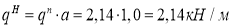
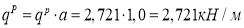
Расчетный изгибающий момент и расчетная поперечная сила в стальной балке равны (1.4, 1.5 соответственно):
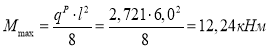
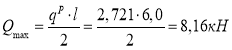
Требуемый момент сопротивления поперечного сечения стальной балки при упругой работе определяется из условия (1.6) [1] п.8.2.1:
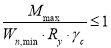
Для заданных условий за материал балки настила принимаем сталь С235, расчетное сопротивление
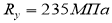
Рассчитываем требуемый момент инерции по формуле (2.7):
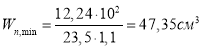
По расчетам принимаем стальную балку двутаврового сечения № 20Б1.
Проверка по нормальным и касательным напряжениям выполняется из условий (1.8, 1.10 соответственно):
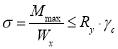
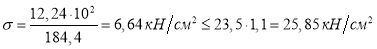
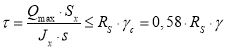
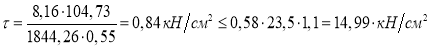
Проверка выполнена и по нормальным напряжениям, и по касательным.
Проверка жесткости (прогиба) стальной балки двутаврового сечения выполняется по формуле (1.12):
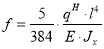
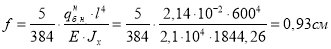
При проверке на прогибы стальной балки должно выполняться условие (1.14):
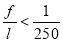
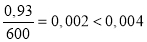
Проверка по прогибам стальной балки проходит, следовательно, окончательно принимаем стальную балку двутаврового сечения № 20Б1.
1.2. Аналитический расчет сталежелезобетонной балки составного сечения на стадии эксплуатации
На стадии эксплуатации плита рассчитывается как железобетонная конструкция с внешней рабочей арматурой из стального профилированного настила и с гибкой стержневой арматурой [4].
Для расчета изгибающего момента от внешней нагрузки и поперечной силы собираем нагрузки на монолитную плиту (таблица 2).
Таблица 2
Сбор нагрузок на монолитную плиту
|
№ п/п |
Вид нагрузки |
Нормативная нагрузка
|
|
Расчетная нагрузка
|
|
Постоянная |
||||
|
1 |
Собственный вес плиты (
|
2,5 |
1,2 |
3 |
|
2 |
Цементно-песчаная стяжка (
|
0,3 |
1,3 |
0,39 |
|
3 |
Паркет |
0,1 |
1,1 |
0,11 |
|
4 |
Подвесной потолок |
0,12 |
1,1 |
0,132 |
|
Итого |
|
|
||
|
Временная |
||||
|
5 |
Перегородки |
0,5 |
1,3 |
0,65 |
|
6 |
Полезная нагрузка |
1,5 |
1,3 |
1,95 |
|
Итого |
|
|
||
|
Всего |
|
|
||
Интенсивность нормативной и расчетной равномерно распределенных нагрузок вычисляем по формулам (1.2, 1.3 соответственно):
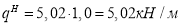
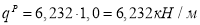
Приведенная площадь железобетонной плиты к металлу будет равна (1.18):
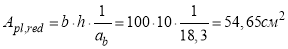
где: коэффициент приведения равен
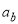
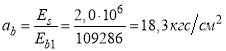
Приведенная площадь сечения равна (1.20):
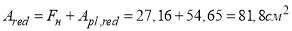
Расстояние от центра тяжести приведенного сечения до нижней грани (1.21):
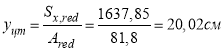
где:
статический момент площади приведенного сечения относительно нижней грани:
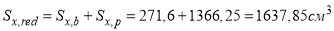
статический момент площади стальной балки относительно нижней грани составного сечения:
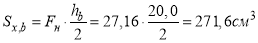
статический момент железобетонной плиты относительно нижней грани составного сечения:
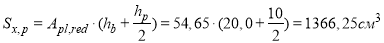
Момент инерции приведенного сечения относительно горизонтальной оси, проходящей через центр тяжести (1.25):
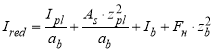
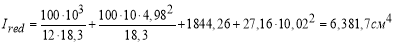
Расчетный изгибающий момент в сталежелезобетонной балке равен (1.27):
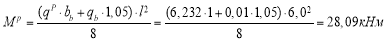
Момент сопротивления приведенного сечения по нижней зоне равен (1.28):
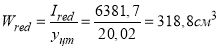
Проверка прочности по условию (1.6):
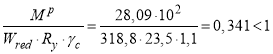
Производим проверку приведенного сечения сталежелезобетонной балки с учетом совместной работы стали и бетона по прогибам по формуле (1.30):
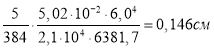
Максимально допустимый прогиб для такой балки, при пролете в 5м, будет равен:
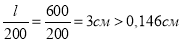
Условие жесткости конструкции выполняется.
1.3. Численный расчет сталежелезобетонного перекрытия
Пространственная модель сталежелезобетонного перекрытия была замоделирована в программном комплексе «ANSYS» (рис. 1) с учетом нелинейных свойств материалов составного сечения перекрытия.
Размеры плиты 6х4 м. Все остальные характеристики и нагрузки такие же, как и в аналитическом расчете. После расчета сталежелезобетонного перекрытия на действие внешней нагрузки были получены максимальные прогибы и напряжения (рис. 2–6).
Рис. 1. Общий вид пространственной модели перекрытия
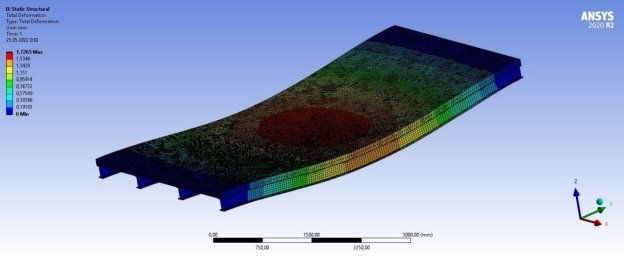
Рис. 2. Прогибы сталежелезобетонного перекрытия от действия внешней нагрузки
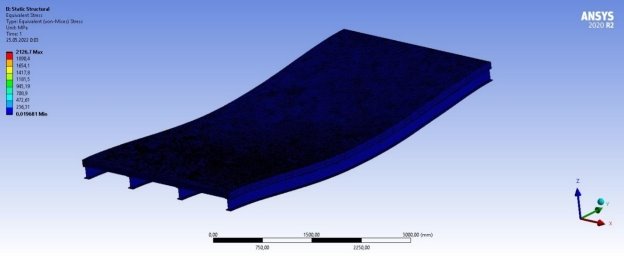
Рис. 3. Максимальные напряжения
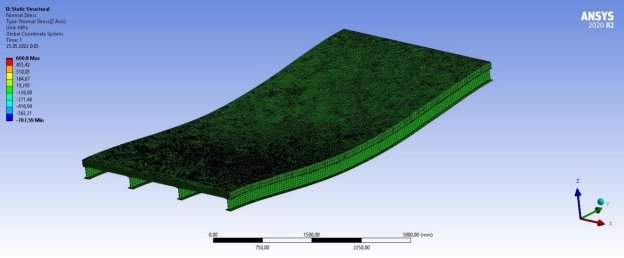
Рис. 4. Максимальные напряжения по оси z

Рис. 5. Максимальные напряжения по оси x
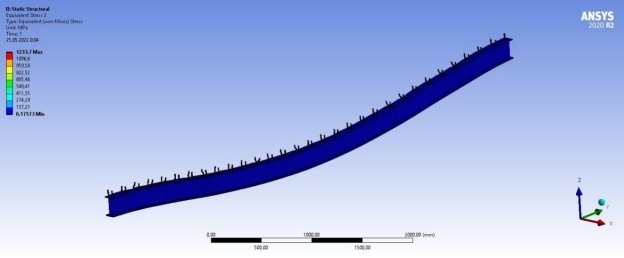
Рис. 6. Максимальные напряжения в отдельной балке
Анализируя полученные результаты аналитического и численного расчетов, становится видно, что увеличение значения прогибов перекрытия приблизительно равно 15 %. Таким образом, делаем вывод, что учет нелинейных свойств материалов составного сечения сталежелезобетонного перекрытия учитывать нужно. Однако стоит отметить, что при расчете конструкций с небольшим пролетом прогибы увеличиваются незначительно. Если же рассматривать пролетные конструкции, например — мостовые сооружения, где часто используются сталежелезобетонные перекрытия с учетом больших по значению нагрузок и различных по характеру воздействия на конструкцию, то в таких случаях учет нелинейных свойств просто необходим. В данном случае аналитический метод расчета сильно уступает численному. Так же в аналитическом методе не учитывается пространственная работа элементов сечения, что склоняет чашу весов в сторону именно численного метода расчета, где учитывается пространственная работа стали и железобетона, работа анкерных устройств и нелинейные свойства материалов перекрытия.
Литература:
- СП 16.13330.2011. «Стальные конструкции». Госстрой России. — М.: ГУП ЦПП, 2002. — 96 с.
- СП 52–101–2003. «Бетонные и железобетонные конструкции без предварительного напряжения арматуры». Госстрой России. — М.: ГУП НИИЖБ, 2004. — 59 с.
- СП 63.13330.2012. «Бетонные и железобетонные конструкции. Основные положения». — Введ. 2013–01–01. — М.: Изд-во стандартов, 2012. — 161 с.
- СП 266.1325800.2016. «Конструкции сталежелезобетонные. Правила проектирования». — Введ. 2017–07–01. — М.: Издательство стандартов, 2017. — 131 с.
- Сталежелезобетонные конструкции перекрытий и покрытий общественных зданий // Реферат работы МНИИТЭП. — 1975. Реф. сб. «Строительные конструкции». — М.: Институт НТ информации, 1975. — 52 с. Сталежелезобетонные конструкции перекрытий и покрытий общественных зданий // Реферат работы МНИИТЭП. — 1975. Реф. сб. «Строительные конструкции». — М.: Институт НТ информации, 1975. — 52 с.
- СТО АРСС 11251254.001–2016. «Сталежелезобетонные конструкции. Правила проектирования». — М.: АРСС, 2016. — 135 с.
- Стрелецкий Н. Н. Сталежелезобетонныепролетныестроениямостов [Composite Steel-and-Concrete Superstructures of Bridges]. Moscow, Transport Publ., 1981, 360 p.