В статье автор ищет наилучший вариант развозки груза в компании, занимающейся курьерской доставкой грузов, при помощи математического моделирования и применения методов оптимизации.
Ключевые слова: математическое моделирование, оптимизация, маршрутизация, кластеризация, грузоперевозки.
Ни для кого не будет являться секретом, что бизнес в процессе своей жизнедеятельности сталкивается с разнообразными видами издержек. Эти затраты необходимо минимизировать для того, чтобы любое производство, предприятие или фирма функционировала как можно более успешно. Одним из таких видов издержек являются транспортные. Они состоят из затрат, которые связаны с работой автотранспортного парка компании. Для их минимизации разработано множество математических моделей, связанных, например, с поиском оптимальных путей.
В данной статье объектом исследования являются транспортные маршруты развозки заказов компании CDEK в городе Санкт-Петербург. Предмет исследования — математические методы оптимизации маршрутов доставки грузов до пунктов выдачи.
В компании CDEK, занимающейся курьерской доставкой грузов, в связи с открытием нового склада в Санкт-Петербурге возникла задача по минимизации транспортных издержек, связанных с доставкой заказов с этого склада до пунктов выдачи, находящихся в черте города. Были предложены несколько вариантов развозки груза, которые изображены в таблице 1.
Таблица 1
Возможные планы развозки грузов
|
План |
Развозка грузов 2 раза в день |
Развозка грузов 3 раза в день |
|
Утренняя развозка |
9:00 (поступление заказов с 0:00 до 11:00) |
9:00 (0:00–7:00) |
|
Дневная развозка |
15:00 (поступление заказов с 11:00 до 24:00) |
13:00 (7:00–15:00) |
|
Вечерняя развозка |
Отсутствует |
17:00 (15:00–24:00) |
|
Максимальный объём груза в одном ТС |
1350 кг (90 % грузоподъёмности ГАЗ 3302) |
1350 кг (90 % грузоподъёмности ГАЗ 3302) |
|
Время на разгрузку на каждом пункте выдачи |
15 минут |
10 минут |
|
Предельное время в пути |
5 часов |
3 часа 30 минут |
В скобках указано промежуток времени поступления заказа за вчерашний день.
На основе статистических данных о заказах, был создан алгоритм формирования заказов со следующими характеристиками:
– существует база потенциальных клиентов в размере 50000 лиц;
– каждую минуту с вероятностью 0,025 % каждый потенциальный клиент может сделать заказ, объём которого подчиняется треугольному распределению с интервалом от 0.1 кг до 15 кг и модой 2 кг. Заказ доставляется в один из пунктов выдачи в Санкт-Петербурге.
Таким образом, для нахождения лучшего плана необходимо решить задачу маршрутизации с ограничением по грузоподъёмности транспортного средства (Capacitated Vehicle Routing Problem — CVRP). Первыми данный тип задач рассмотрели G. Dantzig и J. Ramser в своей работе «The Truck Dispatching Problem» в 1959 году [2]. Для задач CVRP можно использовать точные алгоритмы (перебор всех возможных вариантов), но с увеличением количества точек, которые необходимо объехать, время работы подобных алгоритмов возрастает экспоненциально. Таким образом, для решения задач больших размерностей необходимо использовать эвристические и мета-эвристические алгоритмы, суть которых в поиске близкого к оптимальному решения.
В связи с большой размерностью задачи (в Санкт-Петербурге насчитывается более 250 пунктов выдачи и постаматов), задачу необходимо решать в два этапа:
– кластеризация — объединение объектов в группы (кластеры) таким образом, чтобы эти объекты были как можно более похожи друг на друга внутри одного кластера, нежели при их сравнении с составляющими других кластеров;
– решение задачи коммивояжёра внутри каждого кластера.
Кластеризация была проведена с использованием алгоритма близости, разработанного учёными ИПМ им. М. В. Келдыша РАН [1].
Исходными данными является матрица расстояний A, размерностью n x n (n — число пунктов), со значениями a ij — расстояния между пунктами i и j. Первым делом ищется пункт, наиболее удалённый от всех остальных (в матрице A — строка с наибольшей суммой элементов) — он будет являться первой точкой кластера i 1 . Затем в кластер включается наиближайший к этой точке пункт (минимальный элемент в столбце i 1 матрицы A) — точка i 2 . Третья точка ищется при помощи сложения столбцов i 1 и i 2 , и нахождения номера минимального значения в полученном векторе. Это продолжается, пока спрос клиента i k +1 не будет превышать оставшуюся грузоподъёмность ТС. Остаток — разность грузоподъёмности транспортного средства и суммы величин спроса всех, включённых до этого в кластер, клиентов. Особенностью алгоритма близости как способа кластеризации является то, что число кластеров формируется по ходу работы алгоритма, а не задаётся изначально, что при формировании маршрутов является несомненным плюсом, с учётом того, что каждый новый кластер в данной задаче является новым транспортным средством, арендуемым компанией.
Решение задачи коммивояжёра внутри каждого кластера производится при помощи мета-эвристического алгоритма, который основан на поведении муравьиных колоний.
Рассмотрим, из чего состоит данный алгоритм. Муравьи начинают поиск решения из какой-то начальной точки и выбирают путь, по которому идти, учитывая расстояние между пунктами и количество феромонов, находящихся на этом пути. Другие муравьи будут использовать информацию о лучших путях, так как при переходе муравьёв из одного пункта в другой количество феромонов на этих путях увеличивается, их становится больше, чем путях, которые не являются лучшими. Это сопровождается также выветриванием феромонов в конце каждой итерации, для более быстрого отбрасывания путей, по которым муравьи не проходили, и ускорения процесса поиска оптимальных.
Для применения вышеописанных алгоритмов в среде программирования Wolfram Mathematica была выполнена обработка исходных данных, а именно:
– преобразованы адреса клиентов и склада в географические координаты;
– найдено время переезда между всеми пунктами (клиенты и склад).
Результатами оптимизации внутри каждого кластера являются время нахождения ТС в пути, а также объём груза, который загружается в каждый автомобиль. Они представлены на рис. 1 и 2.
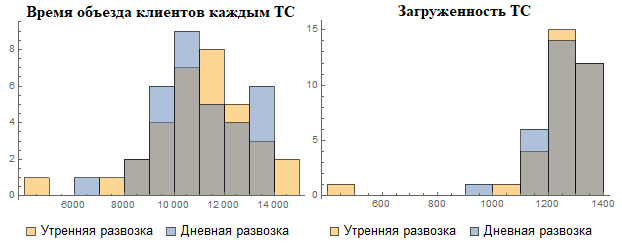
Рис. 1. Результаты оптимизации плана развозки 2 раза в день
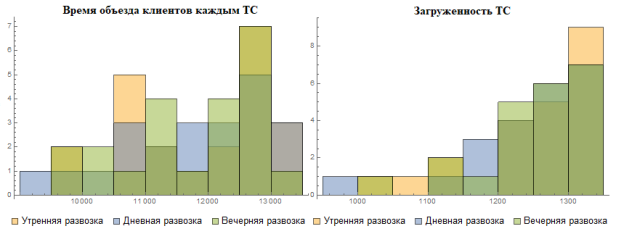
Рис. 2. Результаты оптимизации плана развозки 3 раза в день
В таблице 2 представлены относительная количество ТС, их относительная загруженность и время работы относительно предполагаемого планом.
Таблица 2
Результаты решения CVRP по каждому плану
|
План развозки |
Количество ТС |
Загруженность ТС |
Время работы |
|
2 раза в день |
33 |
83,3 % |
51 % |
|
3 раза в день |
22 |
83,3 % |
82,2 % |
Из полученных результатов видно, что при развозке 2 раза в день наблюдается большой простой автомобилей, что будет являться серьёзным фактором при принятии решения о плане развозки.
Следующий этап — расчёт ежедневных транспортных затрат по каждому плану, которые включают в себя аренду ТС и затраты на топливо. Используемые ГАЗ 3302 2,7 л потребляют топливо АИ-92 при среднем расходе в городских условиях 19 л на 100 км. Стоимость данного бензина — 48 руб. за литр. Аренда каждого ТС обходится 3000 руб. в сутки.
При подсчёте транспортных затрат были получены следующие результаты, отображённые на рис. 3.
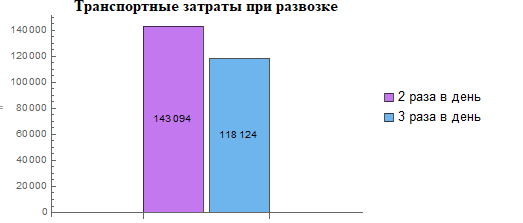
Рис. 3. Расчёт ежедневных транспортных затрат по каждому плану
При развозке 3 раза в день экономия на транспортных затратах составляет около 17,5 %.
Таким образом, было принято решение об использовании плана развозки грузов компании CDEK, основанном на трёхразовой доставке заказов со склада до пунктов выдачи.
В этом помогли использованные и представленные в данной статье следующие математические модели и методы:
– кластеризация с применением алгоритма близости;
– оптимизация путей внутри каждого кластера алгоритмом, основанном на поведении муравьиных колоний.
Литература:
- Смирнов М. И., Хайруллин Р. З. Математические модели, используемые в системе оптимизации доставки товаров автотранспортом «Диспетчер». — М.: ИПМ им. М. В. Келдыша РАН, 2002. — 12 с.
- Dantzig G. B., Ramser J. H. The Truck Dispatching Problem // Management Science. — 1959. — V 6. — P. 80–91.
- CDEK — услуги курьерской службы для частных лиц. [Электронный ресурс]: URL: https://www.cdek.ru/ru (дата обращения 17.05.2022)







