The research uses Mapper algorithm to model and predict traffic accidents through topological data analysis.
Keywords: traffic accidents, topological data analysis, Mapper.
Road transport is a vital component of the national infrastructure, closely related to people's work and life, and which ensures effective and efficient functioning of country's economy.
In the PRC, the number of cars and the length of national highways have increased significantly in recent years. Booming development of the automobile industry and favorable attitude of the government towards online car booking have greatly facilitated people's lives. At the same time, it also brings a series of social problems. This suggests that the topic of data analysis and forecasting of road traffic accidents is important enough to be explored.
Topological data analysis
Topological data analysis (TDA) is a kind of cross data processing technology [1]. It practically applies statistics, algebraic topology, computational geometry, and computer science in the field of data processing. In recent years, with rapid development of various industries and emergence of the Internet, data in numerous domains have constantly emerged at fantastic speed.
Most of these data are characterized with high dimensions and huge quantities.
Efficient and comprehensive usage of such data has become a primary problem in various fields. In order for better study the shape information of high-dimensional data, scholars introduced topology approach into data processing, thus giving birth to topological data analysis technology. It is of value that topology as a branch of geometry concentrates on the shape characteristics of data space. Being originated in the 18th century topology at first, had practical applications mainly in calculations of abstract shapes. But Carlsson proposed a new view [2] on topology and just widened horizons for its applications into the field of data processing. In general topology is concerned with properties of the nature of a data space that tend not to change with small perturbations imposed on its data points. It is well known that in topology, this shape property is strictly defined by such an entity as a 'hole', which is associated with connectivity between data points in one dimension, a circular hole in two dimensions, and a doughnut-shaped hole in three dimensions. High-dimensional 'holes' cannot be observed intuitively, only the number of them can be calculated abstractly. Since these shape properties do not change with continuous transformation, their related information is defined as topological invariants. The same applies to network structures with their vertexes and edges.
Model
Different from traditional intricate methods, a complex constructed by Mapper calculation technique does not directly take the original data point as the vertex, thus avoiding the problem of excessive simplex contained in the final complex. In their paper [3] the authors took the lead in usage Mapper for visualization of high-dimensional data sets. Subsequently, the work [4] presented further studies of application of Mapper complex. The explorers first constructed complex with Mapper, and then extracted the mode that could effectively reveal data component information from sophisticated results, and applied it to analysis in several domain: NBA player performance improvement, organization of election campaign and breast cancer treatment. In addition, they also outlined three key points of the technique which provides effective extraction of data patterns:
1) the topological data analysis technique is independent of the specific coordinate system and its input data points are related to each other;
2) The shape properties studied by topological data analysis techniques do not change with small perturbations of data;
3) The results of topological data analysis techniques are the compression results of shapes. And the crucial point is that just in the nature of this paper there are profound capacities for predicting complications and accidents.
Data
The data we used were collected on the basis of records published at the Weifang (Shandong province, PRC) city's online Data center [5]. The data comprise: weather conditions (fog-rain- snow- normal); dates(months); accident causes (overloading-overspeed-improper driver operation-flat tire-others); accident types; road grades (national road-provincial road- city road-county highway); road serial number; and vehicle types (passenger vehicle -freight vehicle -bus-private car-taxi -others).
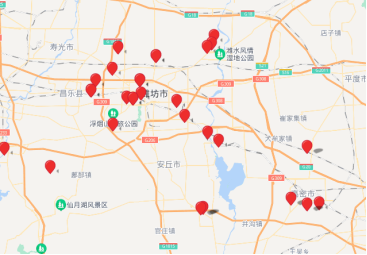
Fig. 1. Map of accidents
Results
The data of the performed experiment mainly consist of three parts: 1) training data set, which was used to find effective parameters; 2) test data set to verify that Mapper technique can be used for category prediction of new data; 3) traffic accident data set with false data, which is used to verify sensitivity of Mapper to fake data. 4) mixed data set with real data and fake data.
While processing with Mapper technique it is implied to use one (or more) filter function, calculate the input data X to obtain one (or more) value, and set two super-parameters, namely resolution (number of intervals, N ) and overlap (in percentage, p ).
The filter function selected in the presented work was UMAP.
We put values for resolution N =7 and overlap p =0.2, and chose DBSCAN clustering function to get the data set complex graphs. The results of the calculations are portrayed on Fig. 2–5.
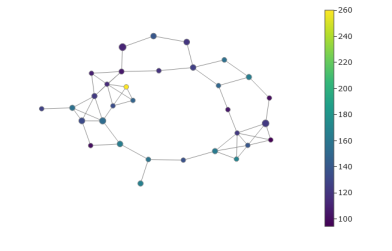
Fig. 2. The complex graph of the training set
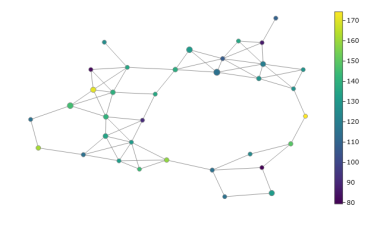
Fig. 3. The complex graph of the test set
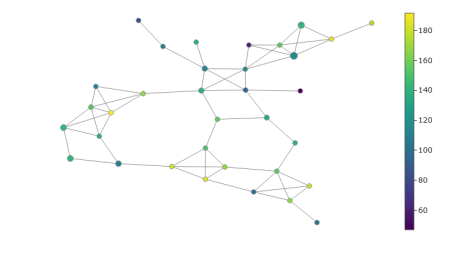
Fig. 4. The complex graph of the false data set

Fig. 5. The complex graph of the mixed data set
Conclusion
The findings of the research demonstrated that one observes essential differences in the complexes of diverse types of data sets in the analysis of traffic accidents. UMAP is efficient enough as dimensionality reduction algorithm. Concerning DBSCAN, it is adopted as the clustering Mapper algorithm, which can be used to classify true and false traffic accidents, however it cannot effectively distinguish real data mixed with false data.
Funding: The reported study was partially funded by RFBR and MECSS, project number 20–57–44002.
References:
1. Carlsson, G. Topological pattern recognition for point cloud data. Acta Numerica, 2014, 23:289–368. doi:10.1017/S0962492914000051
2. Carlsson, G. Topology and data. Bulletin of the American Mathematical Society, 2009, 46 (2):255–308. doi:10.1090/S0273–0979–09–01249-X
3. Singh, G., Memoli, F., Carlsson, G. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition The Eurographics Association, 2007:91–100. doi:10.2312/spbg/spbg07/091–100
4. Lum, P., Singh, G., Lehman, A. et al. Extracting insights from the shape of complex data using topology. Sci Rep, 2013, 3:1236. doi:10.1038/srep01236
- Weifang Public data Open network. Available online: http://wfdata.sd.gov.cn/weifang/ (accessed on 26 May 2022).







