Доказательство значения постоянной всемирного тяготения относительно движения Луны вокруг Земли



Все тела в природе притягиваются друг к другу. Закон, которому подчиняется эта гравитация, был установлен Ньютоном и называется законом всемирного тяготения. Здесь G — гравитационная постоянная, которую также называют коэффициентом пропорциональности, цель постоянного доказательства гравитации — определить движение Луны вокруг Земли и использовать его для решения задач.

Впервые числовое значение постоянной гравитации было определено английским ученым Г. Кавендиш в 1798 году с помощью очень редкого метода крутильных весов.

Два свинцовых шарика массой m (каждый из них 729 г) закреплены на концах коромысла возле проволочных шаров M (по 158 кг каждый) (см.: к рисунку 1 а, б). Коромысло висит на гибкой веревке, через которую можно измерить гравитационную силу шаров. Расстояние между штоками можно изменить с помощью рулевой тяги. Наиболее точное значение определяется различными методами, которая равно G = 6,67 10– ¹¹ Н м ² /кг ²

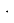
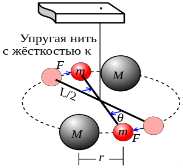
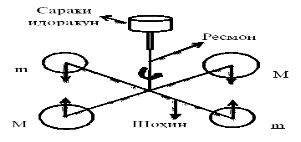
а)б)

Рис. 1

Если m ₁ = m ₂ =1 кг, а r = 1 м, то G число будет равно F. То есть две сферы массой 1 кг, расположенные на расстоянии 1 м друг от друга, притягиваются друг к другу силой 6,67 10– ¹¹ Н.

Этот закон был принят после появления теории Коперника и законов Кеплера, которые определяются как таковые.

Первый закон Кеплера . Все планеты движутся по эллипсу, и в одной из его вершин находится Солнце.

Второй закон Кеплера . Радиусы планет в равные моменты времени рисуют большие равные друг с другом области.

Третий закон Кеплера . Квадраты звездного круга планет вокруг Солнца пропорциональны кубам их эллиптических полутонов. В математическом виде пишется таким образом.

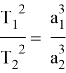
Используя выше упомянутые законы английский ученый И. Ньютон открыл постоянную гравитации, перед учеными того времени встал вопрос: Почему планеты постоянно вращаются вокруг Солнца и меняют свою скорость, как по направлению, так и по величине?».

Ньютон дал полный ответ на этот вопрос. На основании второго закона динамики он установил, что скорость тела изменится тогда, когда к нему будет приложена внешняя сила. Так как Луна вращается вокруг Земли и меняет свою скорость, то можно с уверенностью сказать, что на нее действует какая-то центральная сила, и под действием этой силы тело приобретает ускорение

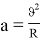
Чтобы определить гравитационную постоянную, мы принимаем орбиту движения Луны вокруг Земли по кругу. Затем в качестве центробежной силы мы принимаем гравитационную силу между Землей и Луной. Величина этой силы равна модулю центробежной силы. Здесь окружность орбиты Луны вокруг Земли равна 27,32 суток, расстояние между Землей и Луной равно 384400 км, а масса Земли равна 6•1024 кг.

Методика доказательства всемирного тяготения

Дано: Решение:

T=27,32с.т =2360448с В соответствии с вышеизложенным

r=3,844 м пишем: F _т = : F _ц

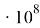
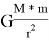
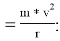
M=6 здесь сила тяготения, равная центробежной силе

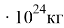
Fт =Fц

G-?

— умножив обе стороны формулы на , получим такую формулу: ; (1)

, то есть: (2)

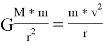
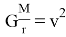
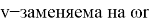
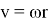
Ставим значение выражения (2) в (1): ;(1)

Обе стороны умножаем на — , находим —

.

(3) Здесь заменяем , тоесть

(4) Ставим значение выражения (4) в (3) и рассчитываем:

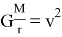
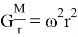
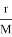
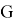
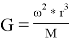
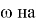
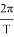
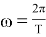
Видно, что значение гравитационной постоянной посредством движения Луны вокруг Земля равна . Образец:

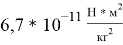
Задача № 1

На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10 ^–5 Н?

Задача № 2

Масса Сатурна 5,7•10 ²⁶ кг, а его радиус— 6•10 ⁷ м. Определите ускорение свободного падения на Сатурне.

Задача № 3

Вычислите ускорение свободного падения и первую космическую скорость у поверхности Луны.

Задачи для самостоятельной работы.

Задача № 1. С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно г? Плотность Земли считайте всюду одинаковой и равной р.

Задача № 2. Масса Марса 6,4•1023 кг, а его радиус— 3,4•107 м. Определите ускорение свободного падения на Марс.

Литература:

1. М.Саъдулоева “Механика, физикаи молекулавӣ ва термодинамика: Дастури таълим барои мактабҳои олӣ. Душанбе: Маориф,1984с.
2. Воронсов.В “ Астраномия” Душанбе.Маориф,1990с.
3. А. П. Рымкевич “ Маҷмӯаи масъалаҳо аз физика” Душанбе. Маориф 1991с
4. Касянов В.А “ Учебник физика-10” ООО “Дрофа” 2001
5. Громов.С.В “ Учебник физика-10” Москва : Просвещение 2003
6. Фриш “ Курс общей физика” Москва : Просвещение 1987
7. Бакулин П. И., Кононович Э. В., Мороз В. И. Курс общей астрономии.
8. Баратов Р. Б., Новиков В. П. Каменное чудо Таджикистана. — Душанбе, Ирфон, 1988. 216 с.
9. Виноградов И. М. Основы теории чисел: Учебник. 2001.
10. Волькенштейн В. С. Сборник задач по общему курсу физики.
11. Воронцов-Вельяминов Б. А., Страут Е. К. Астрономия. 11 класс.