В статье рассматривается процесс определения значения динамического коэффициента для квазистатического метода при расчете зданий и сооружений при прогрессирующем обрушении. Вышеупомянутый процесс рассматривается на примере связевого каркаса пролетом 18,0 м путем сравнения статических расчетов с динамическими, в которых свою очередь учитывается нелинейная и пластическая работы стали. В качестве результатов статьи приводятся выводы насчет влияния динамических расчетов и пластической работы стали на величину динамического коэффициента.
Ключевые слова: прогрессирующее обрушение, коэффициент динамичности, нелинейный статический расчет, пластические шарниры, нелинейный динамический расчет
Вопрос безопасности и надежности зданий и сооружений в последнее время обретает все большее значение при проектировании. В частности, в нормативную документацию стали включать расчетные ситуации на особые (чрезвычайные) воздействия. Одним из таких расчетов является расчет на прогрессирующее обрушение.
В нашей стране основной свод правил [1] регламентирует три методики для расчета на прогрессирующее обрушение — статический, динамический и расчет кинематическим методом теории предельного равновесия. Однако конкретики и подробных указаний как именно выполнять расчет на прогрессирующее обрушения в отечественном СП нет. Стоит отметить, рекомендации по конструктивным решениям по предотвращению прогрессирующего обрушению, которые не имеют указаний для различных конструктивных систем.
При статической методике расчета на прогрессирующее обрушение динамический эффект от выключения из работы несущего элемента моделируется коэффициентом динамичности
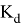
В свою очередь, динамический эффект от выключения несущего элемента при расчете в динамической постановке зависит от длительности удаления несущего элемента из расчетной схемы. Данный способ наиболее точно описывает возникающие усилия в конструкциях. Но в тоже время динамический расчет наиболее трудоемкий, по сравнению со статическим.
И поэтому определение реальной картины напряжённо-деформированного состояния конструкций при динамическом расчете позволило бы определить коэффициент динамичности для более простого статического расчета при прогрессирующем обрушении.
Рассмотрим связевой металлический каркас пролетом 18,0 м с шагом колонн 6,0 м (рис. 1).
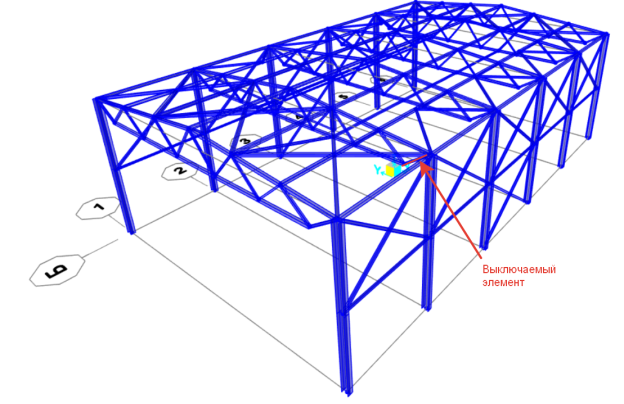
Рис. 1. Стальной каркас пролетом 18,0 м
Расчет выполняется в программном комплексе SAP2000. Данный расчетный комплекс располагает мощным вычислительным ядром, а также имеет удобные функции для внедрения пластических шарниров в расчетную схему.
Конструктивная схема здания — рамно-связевой каркас. В качестве конструктивных мер по предотвращению прогрессирующего обрушения были приняты дополнительные вертикальные связи по всей длине здания.
В качестве выключаемого элемента выбран опорный раскос рядовой фермы (см. рисунок 1). Также необходимо задать длительность выключения данного несущего элемента для динамического расчета. Во избежание возникновения резонанса конструкций, опорный раскос удалится за промежуток времени равный 1/10 периода собственных колебаний. Период был определен модальным расчетом с помощью векторов Ритца, и равен период 0.55с. Также было учтено демпфирование конструкций (рассеивание энергии) равное 2 %.
Важнейшей деталью при динамическом расчете является внедрение пластических шарниров для учета реальной диаграммы (см. рисунок 2) работы стали [2].
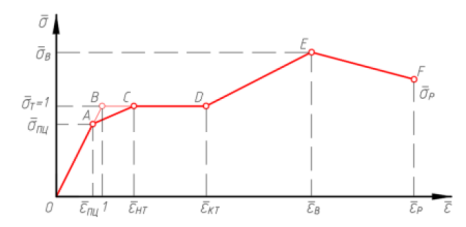
Рис. 2. Диаграмма работы стали
После были смоделированы расчетные ситуации в статической постановке с коэф. Динамичности равным 1 и 2.
При анализе результатов динамического расчета выяснилось следующее. Как видно из рисунка 3 в части элементов, находящихся около удаляемого раскоса, образовались пластические шарниры (зеленые и бирюзовые маркеры) и сталь в данных элементах стала работать на площадке текучести.
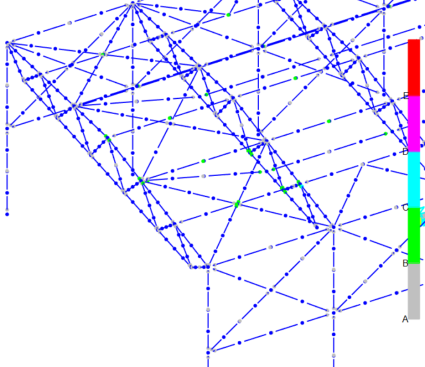
Рис. 3. Образовавшиеся пластические шарниры при выключении опорного раскоса
Далее сравним усилия и перемещения в динамической и статической постановках для некоторых элементов (см. рисунок 4) и узлов с образовавшимися пластическими шарнирами.
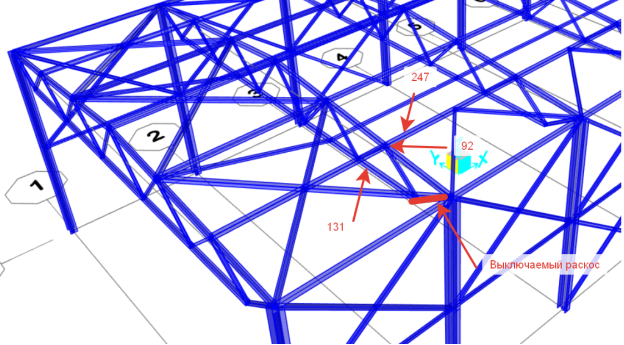
Рис. 4. Анализируемые элементы
При сравнении перемещения узла 92 (рисунок 5) между динамическим и статическими расчетами выясняется, что перемещения в узле наибольшие при динамическом расчете
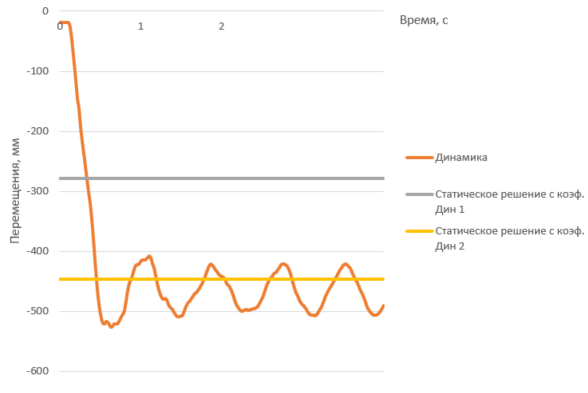
Рис. 5. Диаграмма вертикальных перемещения в узле 92
Похожая ситуация при анализе диаграммы моментов в элементе нижнего пояса 131 (см. рисунок 6) и продольной силы в прогоне (см. рисунок 7)
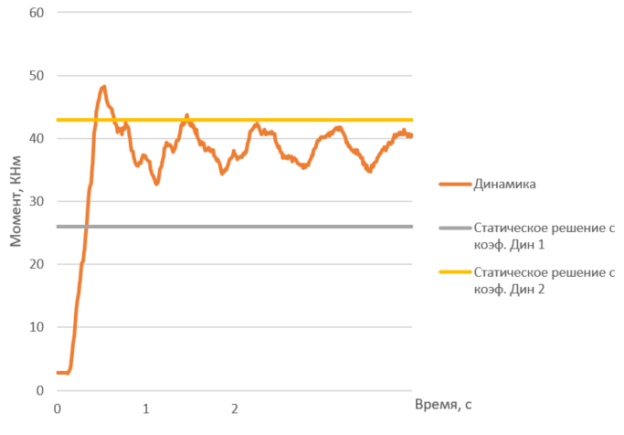
Рис. 6. Диаграмма изгибающего момента в элементе 131 нижнего пояса фермы
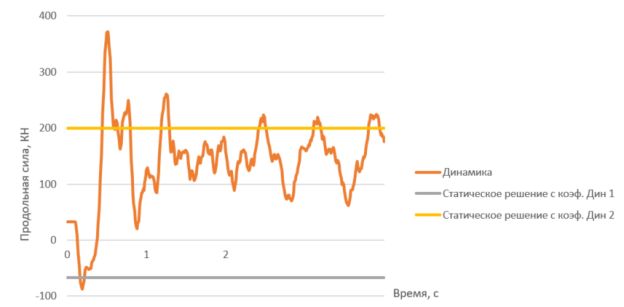
Рис. 7. Диаграмма продольных усилий в 247 элементе (прогон)
Рассматривая полученные данные, можно сказать, что пластическая стадия работы стали существенно сказывается на результатах расчета. Образовавшиеся пластические шарниры перераспределяют усилия на соседние конструкции. Но также стоит отметить, что в данной расчетной схеме не были предусмотрены конструктивные решения по предотвращению прогрессирующего обрушения по покрытию. Соответственно при выключении из работы опорного раскоса ферм некоторые конструкции излишне напряжены и сталь доходит до зоны самоупрочнения, что в свою очередь недопустимо. Для более корректной оценки коэффициента динамичности необходимо предусмотреть усиление покрытия. А также рассмотреть другие элементы для выключения из расчетное схемы, например, панель нижнего пояса, крайняя и рядовая колонна здания.
Литература:
1. СП 385.1325800.2018 «Защита зданий и сооружений от прогрессирующего обрушения. Правила проектирования. Основные положения (с Изменениями № 1, 2»
2. СП 16.13330.2017 «Стальные конструкции. Актуализированная редакция СНиП II-23–81*" (с Поправками, с Изменениями № 1, 2,3)







