В настоящей статье затрагиваются Г-, Т-, П-образные пассивные k-фильтры низких частот (активные фильтры в настоящей статье не рассматриваются), рассматривается работа таких фильтров, приводятся графики амплитудно-частотных характеристик, показываются формулы характеристических сопротивлений для каждых фильтров.
Ключевые слова: электрические фильтры, АЧХ, ФНЧ, ФВЧ, индуктивность, емкость, ряд Фурье, гармонический сигнал.
В современном мире, при очень развитой полупроводниковой электронике, получили распространение так называемые электрические фильтры (далее — фильтры), построенные, в большинстве случаев, из пассивных реактивных компонентах — линейной катушки индуктивности и линейного конденсатора.
Работа фильтров основана на зависимости реактивного сопротивления элементов от частоты:
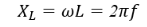
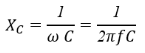
Фильтрами низких частот
называют фильтры, пропускающие через себя, в общем случае, без изменений сигнал от 0 до
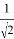
На рис. 1 приведены типичные конструкции фильтров низких частот.
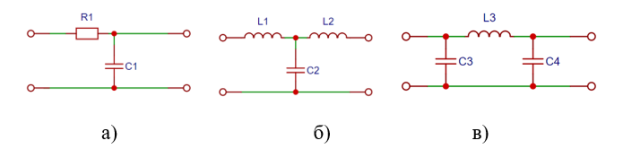
Рис. 1. Конструкции фильтров нижних частот: а) Г-образный; б) Т-образный; в) П-образный
Рассмотрим на примере работу Т-образного фильтра нижних частот. (рис. 2)
Поскольку в составе фильтра имеются только реактивные элементы — фильтр относится к типу k-фильтров, так для таких фильтров выполняется условие симметричности: при изменении частоты характер продольного реактивного сопротивления обратен характеру поперечного реактивного сопротивления. Другими словами, например, при увеличении частоты индуктивное сопротивление увеличивается, а емкостное сопротивление — уменьшается.
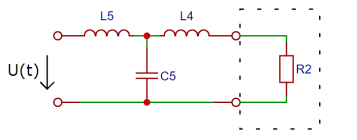
Рис. 2. Испытательная схема
Пусть на входных зажимах имеется напряжение, изменяющееся по закону:
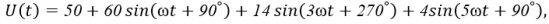
а параметры цепи будут равны:
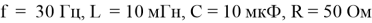
Исходя из данных условий, опуская весь математический аппарат, получим закон изменения во времени напряжения на нагрузки:
Составим график зависимости напряжения от времени для двух известных законов и получим следующую ситуацию:
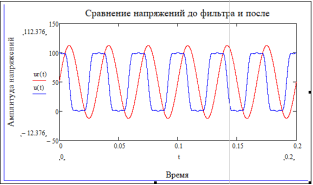
Рис. 3. График напряжений на входе и на нагрузке
Из графика видно, что фильтр подавил токовые составляющие высших гармоник. Составим линейчатые спектры амплитуд входного напряжения и напряжения на нагрузки (рис. 4):
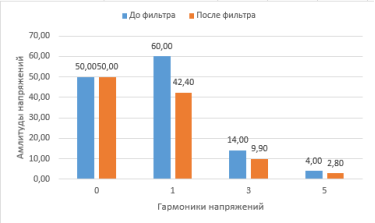
Рис. 4. Линейчатый спектр амплитуд напряжений
Для более глубокого анализа подобного фильтра, примем ФНЧ как четырехполюсник (рис. 5) и найдем его характеристическое сопротивление.
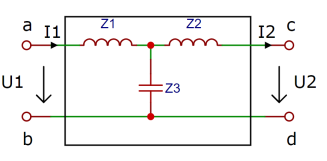
Рис. 5. Представление фильтра как четырехполюсника
Поскольку фильтр является симметричным — его продольные и поперечные сопротивления попарно равны — достаточным условием для поиска характеристического сопротивления (7) достаточно найти коэффициенты B, C по формулам четырехполюсника A-формы [1]:
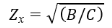
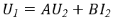
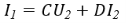
Вариантов поиска коэффициентов четырехполюсника много, равно как и форм их записи, подробнее про формы записи можно ознакомится в авторитетных учебниках.
Найдя коэффициенты по формулам (6) и (7) и подставив в (5) получим:
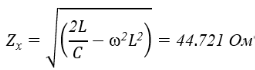
Поскольку пассивные фильтры являются частотно-зависимыми (сопротивления их компонентов зависят от частоты), то при малейшем изменении частоты необходимо согласовывать нагрузку (в отличии m-фильтров, где существует небольшой диапазон частот, при котором согласование не требуется). Для симметричных k-фильтров нижних частот сопротивление нагрузки нужно выбирать в зависимости от характеристического сопротивления (далее — Zx) во избежание потерь фильтрующих свойств самого фильтра.
Построим график зависимости
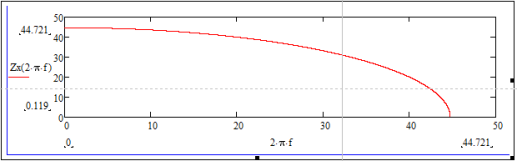
Рис. 6. График зависимости
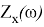
Поскольку необходимо, чтобы фильтр работал до частоты среза (
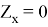
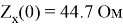
В данном примере видно, что фильтр подавляет токовые составляющие высших гармоник не сильно эффективно, т. е. наблюдается не крутой спад амплитудно-частотной характеристики. Для того, чтобы этого избежать, нужно либо увеличить емкость конденсатора, чтобы он зашунтировал нагрузку, что бывает неэффективно, либо заменить Т-образный фильтр на П-образный фильтр, получив уже крутость амплитудо-частотной характеристики, большую эффективность за счет создания дополнительных падений напряжений на элементах, не сильно увеличивая габариты и стоимость устройств.
Поскольку для современных задач в области обработки сигналов пассивные электрические фильтры были вытеснены активными, с применением операционных усилителей, пассивные фильтры очень широко применяются в силовой электронике, например, фильтрации блоков питания.
Литература:
- Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи / Л. А. Бессонов. — 11-е изд., переработанное и дополненное. — Москва: Юрайт, 2013. — 701 c. — Текст: непосредственный.







