В статье автор рассказывает об особенностях накопления случайности при помощи комбинирования различных генераторов псевдослучайных чисел и приводит результаты экспериментов, подтверждающих их.
Ключевые слова: накопление случайности, генератор псевдослучайных чисел (ГПСЧ), комбинированный ГПСЧ, сложение по модулю 2, XOR
В своей предыдущей статье «Накопление случайности в генераторах псевдослучайных чисел», опубликованной 14 февраля 2022 года в данном журнале, я рассматривал способ увеличения случайности различных генераторов псевдослучайных чисел (ГПСЧ) при помощи логической функции «сложение по модулю 2» (XOR, «исключающее или», ⊕). В ней не рассматривался вариант накапливания случайности при помощи комбинирования различных ГПСЧ, чему и посвящена данная статья. [1]
Условно ГПСЧ можно представить как некий «механизм», получающий на входе энтропию, а выдающий псевдослучайные числа. [2] Графически схема ГПСЧ изображена на рисунке 1.

Рис. 1. Графическая схема ГПСЧ
В конструкции любого ГПСЧ есть нечто, что не дает ему быть абсолютно случайным. Совершенно неважно, что это за причина, и какого она характера. Важен сам факт ее наличия. Эту причину можно изобразить в виде черного квадрата внутри условного графического обозначения (УГО) ГПСЧ. Это отображено на рисунке 2.
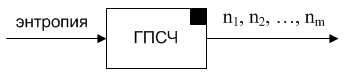
Рис. 2. Графическая схема ГПСЧ
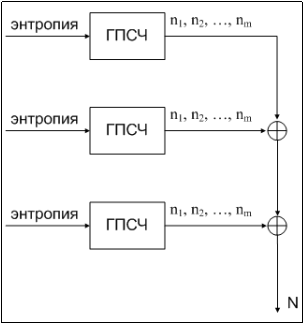
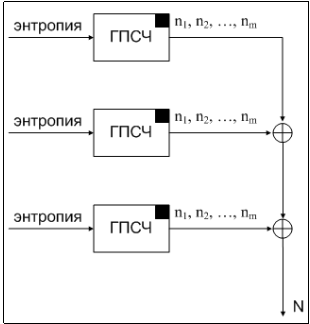
Различные ГПСЧ могут увеличивать случайность друг друга при помощи «перемешивания» сгенерированных ими чисел логической функцией ⊕. Таким образом, мы превращаем множество ГПСЧ в один большой ГПСЧ. Этот принцип схематично изображен на рисунке 3 (а). Объединяя все ГПСЧ в один, мы получаем один большой ГПСЧ, имеющий все причины «не случайности» всех ГПСЧ в него входящих. Наглядно это изображено на рисунке 3 (б).
|
а) |
б) |
Рис. 3. Комбинированный ГПСЧ
Случайность ГПСЧ (S) рассчитывается по следующей формуле [1]:
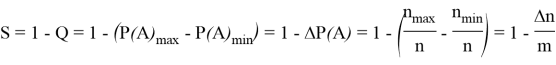
Для доказательства данной гипотезы был проведен следующий опыт: на 5 ГПСЧ было осуществлено накопление случайности при помощи перемешивания от 1 до 11 чисел логической функцией XOR. Для эксперимента были выбраны следующие ГПСЧ: «rand» [3], «random_int» [4], «random_bytes» [5], «openssl_random_pseudo_bytes» [6], «uniqid» [7]. Результаты представлены в таблице 1.
Таблица 1
Результаты накопления случайности на различных ГПСЧ
|
№ |
Генераторы псевдослучайных чисел |
||||
|
Rand |
Random_int |
Random_bytes |
openssl_random_pseudo_ bytes |
uniqid |
|
|
1 |
0,998791 |
0,99894 |
0,995726 |
0,995089 |
0,998686 |
|
2 |
0,899095 |
0,899844 |
0,899472 |
0,899605 |
0,898847 |
|
3 |
0,903935 |
0,90343 |
0,90306 |
0,926265 |
0,903837 |
|
4 |
0,901062 |
0,901256 |
0,900828 |
0,928027 |
0,901606 |
|
5 |
0,901522 |
0,901209 |
0,901109 |
0,93173 |
0,901887 |
|
6 |
0,901048 |
0,901427 |
0,900787 |
0,93374 |
0,901084 |
|
7 |
0,901026 |
0,901012 |
0,90012 |
0,935063 |
0,900913 |
|
8 |
0,901609 |
0,901019 |
0,900373 |
0,935453 |
0,901518 |
|
9 |
0,901332 |
0,900833 |
0,900379 |
0,936186 |
0,901094 |
|
10 |
0,901136 |
0,901741 |
0,900491 |
0,901031 |
0,900907 |
|
11 |
0,901407 |
0,901295 |
0,900348 |
0,899991 |
0,901212 |
Далее было осуществлено накопление случайности при помощи комбинирования ГПСЧ. В комбинировании участвовали следующие ГПСЧ: «rand» [3], «random_int» [4], «random_bytes» [5], «openssl_random_pseudo_bytes» [6], «uniqid» [7], а также ГПСЧ, встроенные в языки программирования С [8], C++ [9], C# [10], JavaScript [11], Pascal [12] и BASIC [13].
Накопление случайности на комбинированном ГПСЧ происходит по принципу добавления ГПСЧ: в каждом новом испытании добавлялся один новый генератор, после чего проходит вычисление случайности всей конструкции (комбинированного ГПСЧ). Данные представлены в таблице 2.
Таблица 2
Накопление случайности на комбинированном ГПСЧ
|
№ |
Добавляемый ГПСЧ |
S добавляемого ГПСЧ |
S |
|
1 |
Rand |
0,999337 |
0,999337 |
|
2 |
Random_int |
0,999506 |
0,999547 |
|
3 |
Random_bytes |
0,995126 |
0,998175 |
|
4 |
openssl_random_pseudo_bytes |
0,995759 |
0,99762975 |
|
5 |
uniqid |
0,998916 |
0,9980888 |
|
6 |
C |
0,54151 |
0,922173167 |
|
7 |
C++ |
0,440747 |
0,918811571 |
|
8 |
C# |
0,88822 |
0,915072 |
|
9 |
JavaScript |
0,999309 |
0,924431666 |
|
10 |
Pascal |
0,998633 |
0,9319596 |
|
11 |
BASIC |
0,876855 |
0,934851818 |
На основе полученных данных были вычислены 2 параметра для каждого ГПСЧ: уровень накопленной случайности (ΔS) и коэффициент накопления случайности (k) по следующим формулам:
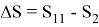
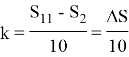
где: ΔS — уровень накопленной случайности, S 11 — случайность из 11 строки таблицы, S 2 — случайность из 2 строки таблицы, k — коэффициент накопления случайности.
Значения S 2 и S 11 берутся в таблицах 1 и 2, индекс буквы S обозначает номер строки таблицы.
Результаты эксперимента представлены в таблице 3.
Таблица 3
Результаты проведенного эксперимента
|
Название ГПСЧ |
Параметры ГПСЧ |
|||
|
S 11 |
S 2 |
ΔS |
k |
|
|
Rand |
0,9014070 |
0,8990950 |
0,0023120 |
0,0002312 |
|
Random_int |
0,9012950 |
0,8998440 |
0,0014510 |
0,0001451 |
|
Random_bytes |
0,9003480 |
0,8994720 |
0,0008760 |
0,0000876 |
|
openssl_random_pseudo_ bytes |
0,8999910 |
0,8996050 |
0,0003860 |
0,0000386 |
|
uniqid |
0,9012120 |
0,8988470 |
0,0023650 |
0,0002365 |
|
Комбинированный |
0,9348518 |
0,9995470 |
-0,0646952 |
-0,0064695 |
Согласно полученным данным, всем ГПСЧ, кроме комбинированного, удалось накопить случайность. Тем не менее, стоит отметить, что накопление случайности на комбинированном генераторе произойдет только при многократном увеличении числа ГПСЧ, что доказывает превосходство способа накопления случайности на одном генераторе при помощи ⊕.
Выводы:
- При комбинировании ГПСЧ происходит увеличение количества причин того, почему данный ГПСЧ не идеальный. Количество причин равно количеству причин всех входящих в него генераторов.
- Увеличение случайности при помощи комбинирования различных ГПСЧ менее эффективно, нежели накапливание случайности путем перемешивания сгенерированных чисел одним и тем же генератором логической функцией ⊕.
Литература:
- Чайко, В. И. Накопление случайности в генераторах псевдослучайных чисел. / В. И. Чайко. — Текст: непосредственный // Исследования молодых ученых: материалы ХXХII Международной научной конференции. — Казань: Молодой ученый, 2022. — С. 10–15. URL: https://moluch.ru/conf/stud/archive/418/16988/ (дата обращения: 26.05.2022).
- Смарт, Н. Криптография / Н. Смарт. — М.: Техносфера, 2005. — 528 c. — Текст: непосредственный.
- rand. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.rand.php (дата обращения: 25.05.2022).
- random_int. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.random-int.php (дата обращения: 25.05.2022).
- random_bytes. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.random-bytes.php (дата обращения: 25.05.2022).
- openssl_random_pseudo_bytes. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.openssl-random-pseudo-bytes.php (дата обращения: 25.05.2022).
- uniqid. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.uniqid.php (дата обращения: 25.05.2022).
- ISO/IEC 9899:2018 Information technology — Programming languages — C. — Текст: электронный // https://www.iso.org: [сайт]. — URL: https://www.iso.org/standard/74528.html (дата обращения: 25.05.2022).
- C++. — Текст: электронный // C++: [сайт]. — URL: https://isocpp.org (дата обращения: 25.05.2022).
- Документация по C#. — Текст: электронный // Microsoft: [сайт]. — URL: https://docs.microsoft.com/ru-ru/dotnet/csharp (дата обращения: 25.05.2022).
- JavaScript.com by Pluralsight. — Текст: электронный // JavaScript.com: [сайт]. — URL: https://www.javascript.com (дата обращения: 25.05.2022).
- Система программирования PascalABC.NET. — Текст: электронный // PascalABC.NET: [сайт]. — URL: http://www.pascalabc.net (дата обращения: 25.05.2022).
- Liberty BASIC v4.5.1. — Текст: электронный // Liberty BASIC: [сайт]. — URL: https://www.libertybasic.com (дата обращения: 25.05.2022).







