В данной статье исследуется возможность моделирования популяции при помощи клеточного автомата. Прогнозирование является одним из важнейших методов при борьбе с вымиранием видов животных и при помощи компьютерных технологий, появляется возможность более автоматизировано и эффективно прогнозировать популяцию существ в их среде обитания.
Ключевые слова: клеточные автоматы, математическое моделирование, прогнозирование .
Прогнозирование и моделирование позволяет ученым предотвратить возможные отрицательные события или снизить ущерб от них. Это могут быть как природные и техногенные катастрофы, так и имитирование исторических данных, для анализа их изменения. Поэтому оно является одним из важнейших методов для современных исследователей. При помощи компьютеров появилась возможность задействовать этот метод более эффективно и точно. Одним из самых известным вариантов является клеточный автомат. При его помощи становится возможным реализация прогноза по распространению популяции каких-либо видов животных в рамках определенной системы. Например, на основе клеточного автомата была создана модель, которая демонстрирует особенности формирования границ государств [1], некоторые усредненные результаты которой достаточно точно совпадают с историческими или нынешними данными, пример изображен на рис. 1.
![Пример усредненного результата моделирования [1]](https://moluch.ru/blmcbn/92890/92890.001.png)
Рис. 1. Пример усредненного результата моделирования [1]
Для начала стоить дать определение, что же такое клеточный автомат. Клеточный автомат — дискретная модель, изучаемая в математике, теории вычислимости, физике, теоретической биологии и микромеханике. Представляет собой сетку произвольной размерности, каждая клетка которой в каждый момент времени может принимать одно из конечного множества состояний, что в нашем случае позволяет создавать условия с неограниченным количеством параметров, а точнее множественных популяций [2].
Для того, чтобы сконцентрироваться на разработке конечной программы выполняющую моделирование, для визуализации был задействован графический игровой движок Unity [3]. За основу клеточного автомата изначально были взяты правила “Игра Жизнь” как заведомо проверенные и рабочие. В правилах отсутствую так называемые “Агрессоры”, иначе говоря клетки хоть и разных популяций не претендуют на захват друг друга, отчего система быстро приходит в стабильное состояние. Так же, если бы в жизни все было линейно, а иначе, предсказуемо, тогда человеку не понадобились никакие прогнозирующие методы. Поэтому в систему распространения популяций был добавлен элемент генератора псевдослучайных чисел, что позволило создать систему, в которой захват клетки определенной популяцией будет возможен лишь с вероятностью 50 процентов. Для реализации описанного алгоритма была разработана система, позволяющая моделировать неограниченное количество популяций, поэтому будут показаны тесты разных вариаций. Созданная программная модель не претендует на высокую точность, так как на ее генерацию, влияет лишь одно свойство, что может избавить систему от линейности, когда как на точность влияет именно детерминированность факторов [4].
Для начала работы программы требуется выставить начальные точки образования популяций как на рис. 2, слева. После запуска моделирования, шаг за шагом генерируется популяция по описанным правилам, в конце которой мы получаем стабильную систему как на рис. 2, справа.
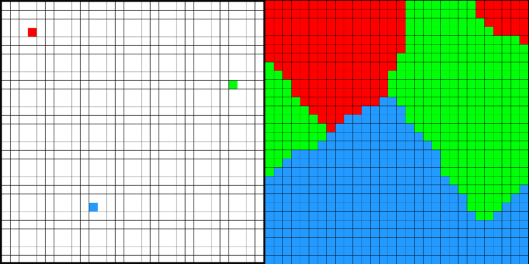
Рис. 2. Система с тремя популяциями
Также видно, что некоторые популяции разделены между собой по разным частям поля. Это происходит из-за того, что несмотря на то, что мы видим поле как прямое, с точки зрения вычислений оно является схожим с поверхностью тора, от чего клетки при переходе на край выходят с другого края. Эта система схожа с реализацией клеточного автомата “Игра жизнь” [5]. Далее на рис. 3 и рис. 4. Представлены результаты моделирования для четырех и шести популяций, соответственно.
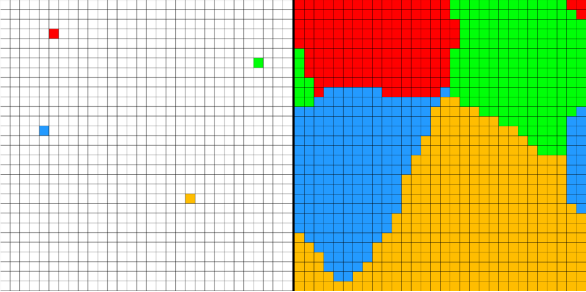
Рис. 3. Система с четырьмя популяциями
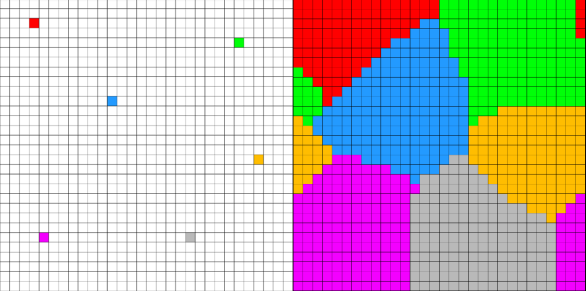
Рис.4. Система с шестью популяциями
Для последней системы (рис. 4) был составлен график количества захваченных клеток каждой популяции в течении двенадцати ходов, который можно увидеть на рис. 5. Так же было проведено несколько дополнительный исследований, чтобы определить, зависит ли размер конечной популяции в зависимости от ее положения на поле (рис. 6, рис. 7).
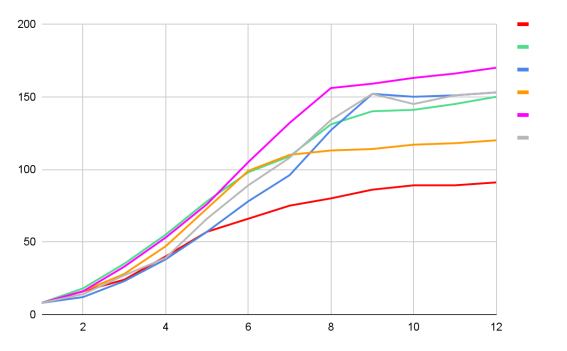
Рис. 5. График роста количества захваченных популяциями клеток
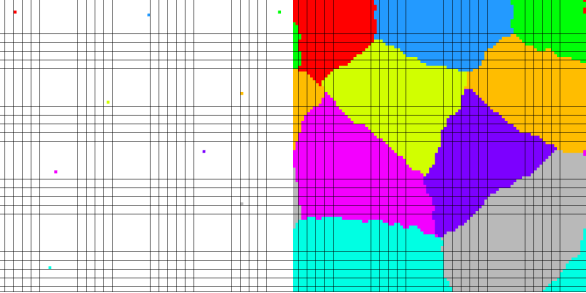
Рис. 6. Система с шестью популяциями, второй тест
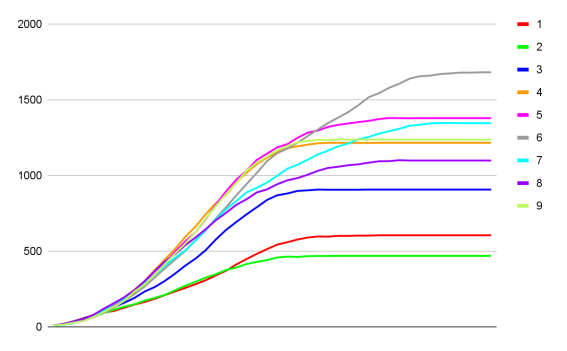
Рис. 7. График роста количества захваченных популяциями клеток
Как можно заметить, самой маленькой популяцией является зеленая. Для того чтобы подтвердить зависимость результатов от расположения начальных точек популяций, были проведены еще 2 тестирования, в каждом из которых начальная точка зеленой популяции была сдвинута на 10 клеток по обеим осям ближе к центру (рис. 8). Влияние изменений стартового положения видно из графиков на рис. 9 и рис. 10.
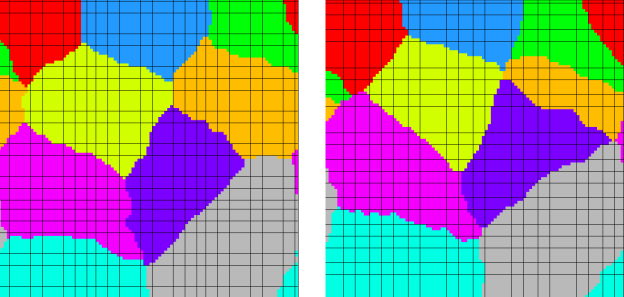
Рис. 8. Смещение начальной точки
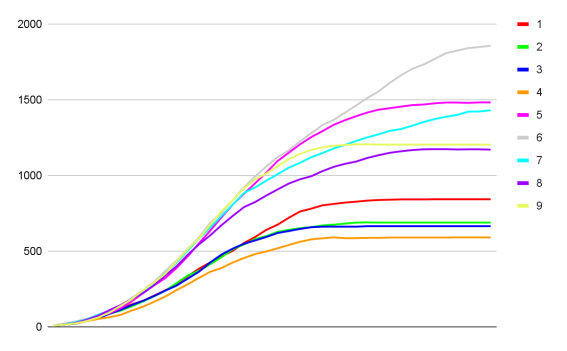
Рис. 9. Первое смещение начальной тчоки зеленой популяции
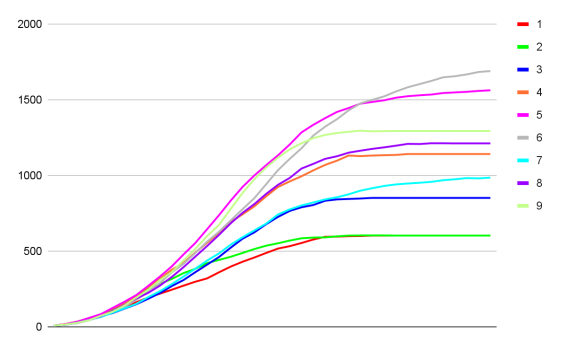
Рис. 10. Второе смещение начальной тчоки зеленой популяции
По результатам первого теста можно сделать вывод, что от сдвига начальной популяции ее размер действительно вырос. Но после второго можно увидеть, что сдвиг на еще десять клеток не сильно повлиял на зеленую популяцию, зато повлиял на близкую к ней оранжевую.
По результатам тестирования можно сказать, что в системе размер популяции зависит не от ее начальной позиции по отношению к центру, а от расположения соседних популяций. В результате получилось реализовать простейшую модель популяций, без агрессивных особей не независящих от их расположения относительно центра. Распространение с учетом заданных данных и генератором случайных чисел позволяет смоделировать правдоподобную картину в определенный момент времени.
Литература:
- Арабей, С. О. Имитационное моделирование аграрных обществ методом клеточного автомата / С. О. Арабей, И. С. Нилов; научный руководитель Ю. В. Рождественский // Сборник трудов IV Всероссийского конгресса молодых ученых, Санкт-Петербург, 07–10 апреля 2015 года. — Санкт-Петербург: Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, 2015. — С. 27–29. — EDN VEFJVJ.
- Простейшие клеточные автоматы и их практическое применение. — Текст: электронный. // Хабр: [Сайт]. — 2016. — URL: https://habr.com/ru/post/273393/ (дата обращения: 01.03.2022).
- Сорокин, А. А. Графические движки как средство моделирование лабораторий / А. А. Сорокин, Е. А. Яковлева // Математические методы и модели в высокотехнологичном производстве: Тезисы докладов I Международного форума, Санкт-Петербург, 10–11 ноября 2021 года. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2021. — С. 164–165. — EDN TPPECX.
- Рождественский, Ю. В. Квантово-механическая интерпретация исторической динамики в рамках моделирования границ аграрных государств / Ю. В. Рождественский, Р. А. Коваленко // Математические методы и модели в высокотехнологичном производстве: Тезисы докладов I Международного форума, Санкт-Петербург, 10–11 ноября 2021 года. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2021. — С. 257–258. — EDN LOJOCC.
- Поиграем в жизнь. — Текст: электронный. // Хабр: [Сайт]. — 2009. — URL: https://habr.com/ru/post/63848/ (дата обращения: 01.03.2022).







